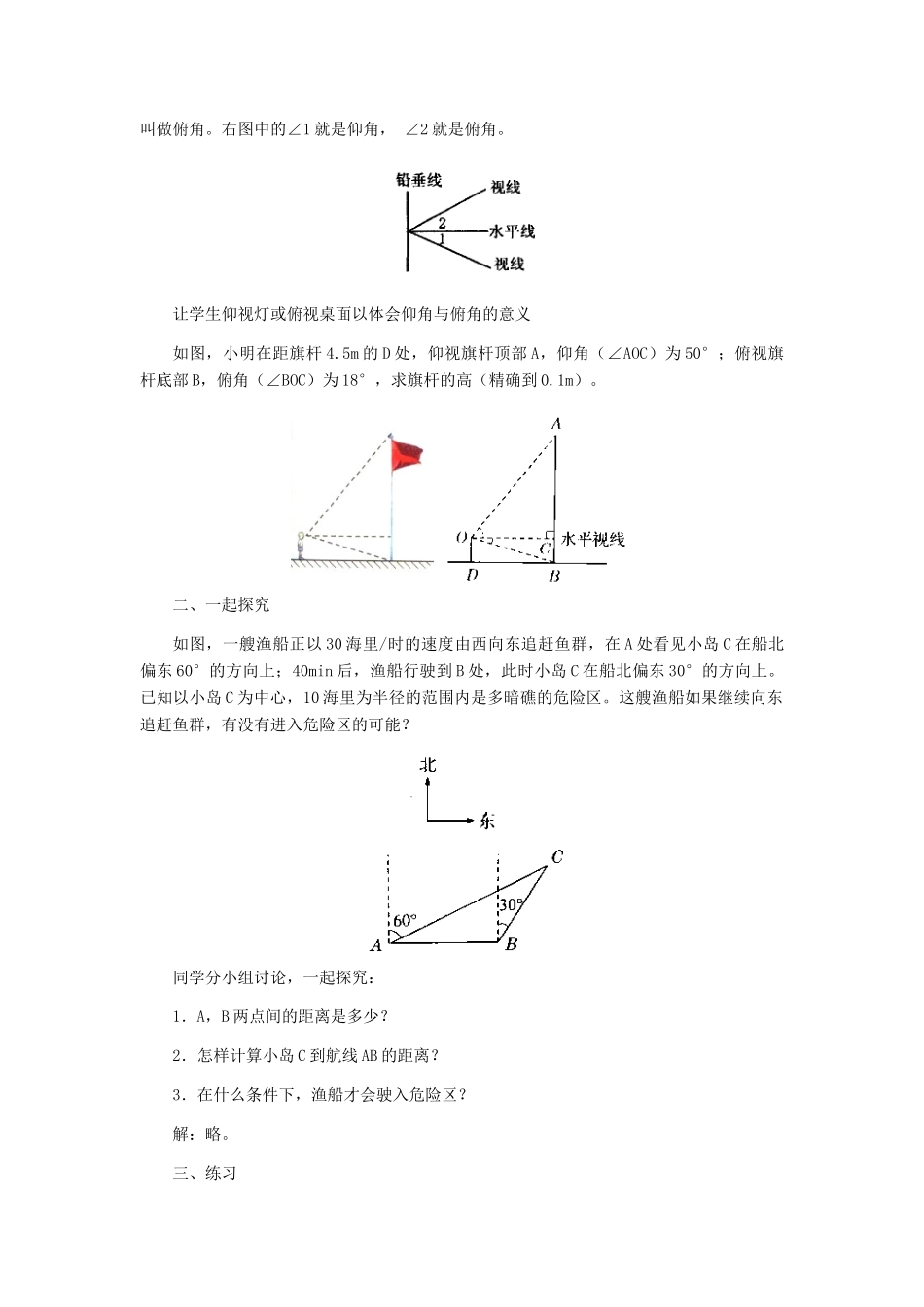
锐角三角函数的应用教学设计教学设计思想数形结合是重要的思想方法,而本章内容是体现数形结合思想的理想材料。本节主要内容是运用锐角三角函数解决实际问题,解题的过程充分体现了数形结合思想,应引导学生根据问题情境画出图形,把实际问题抽象为几何问题,再通过图形找出直角三角形中边角之间的关系。教学目标知识与技能:1.利用锐角三角函数,能够解决与直角三角形有关的实际问题,从而进一步把数形结合起来。2.能描述出仰角、俯角、坡度、水平距离、垂直距离等概念,并能在具体问题中正确运用。过程与方法:1.结合锐角三角函数在工程度量、测量距离等各方面的应用,学会数学建模思想。2.通过对直角三角形的构造过程,学会问题的转化意识。情感态度价值观:通过本节课的学习,培养解决实际问题的能力及用数学的意识,在数学应用的过程中学会问题的转化意识,逐步形成数学价值观。教学重难点重点:用锐角三角函数解决实际问题难点:把实际问题中的数量关系抽象为直角三角形中元素之间的关系。教学媒体多媒体课时安排2课时教学过程设计第一课时一、观察与思考如图,从下往上看,视线与水平线的夹角叫仰角,从上往下看,视线与水平线的夹角叫做俯角。右图中的∠1就是仰角,∠2就是俯角。让学生仰视灯或俯视桌面以体会仰角与俯角的意义如图,小明在距旗杆4.5m的D处,仰视旗杆顶部A,仰角(∠AOC)为50°;俯视旗杆底部B,俯角(∠BOC)为18°,求旗杆的高(精确到0.1m)。二、一起探究如图,一艘渔船正以30海里/时的速度由西向东追赶鱼群,在A处看见小岛C在船北偏东60°的方向上;40min后,渔船行驶到B处,此时小岛C在船北偏东30°的方向上。已知以小岛C为中心,10海里为半径的范围内是多暗礁的危险区。这艘渔船如果继续向东追赶鱼群,有没有进入危险区的可能?同学分小组讨论,一起探究:1.A,B两点间的距离是多少?2.怎样计算小岛C到航线AB的距离?3.在什么条件下,渔船才会驶入危险区?解:略。三、练习课本第121页练习的第l、2题。四、小结本节课我们学习了有关仰角、俯角的解直角三角形的应用题,对于这些问题,一方面要把它们转化为解直角三角形的数学问题,另一方面,针对转化而来的数学问题选用适当的数学知识加以解决。五、作业课本121页3、4题六、板书设计锐角三角函数的应用(1)仰角与俯角例题练习第二课时一、引入新课如图所示,斜坡AB和斜坡A1B1哪一个倾斜程度比较大?显然,斜坡A1Bl的倾斜程度比较大,说明∠A1>∠A。从图形可以看出,>,即tanAl>tanA。在修路、挖河、开渠和筑坝时,设计图纸上都要注明斜坡的倾斜程度。我们通常把坡面的铅直高度h和水平宽度l的比叫做坡面的坡度(或坡比),坡面与水平面的夹角叫做坡角。坡角通常用α表示,有tanα=。显然,坡度越大,坡角越大,坡面就越陡。二、例题讲解例1.如图,铁道路基的横断面为等腰梯形ABCD,根据图中标出的数据计算路基下底的宽和坡角(精确到1′)分析:1.在等腰梯形ABCD中,如何求AD?2.坡面AB的垂直高度和水平宽度与坡长、坡角有什么关系?3.能否求出水平宽度?学生根绝上述分析自主探究,探索解题思路,写出解决问题的过程。解:如图,等腰梯形ABCD为路基横断面的示意图作BE⊥AD,垂足为E。在Rt△ABE中,BE=4,tanα=,即。所以α≈38°40′,AE=5。所以AD=BC+2AE=10+2×5=20(m)。答:路基下底的宽为20m,坡角约为38°40′。三、做一做如图,某水库大坝的横截面是梯形ABCD,坝顶宽CD=3m,斜坡AD=16m,坝高为8m,斜坡BC的坡度为。求斜坡AD的坡角α和坝底的宽AB(精确到0.01m)。四、练习课本第123页的练习。五、小结会知道坡度、坡角的概念能利用解直角三角形的知识,解决与坡度、坡角有关的实际问题,特别是与梯形有关的实际问题,懂得通过添加辅助线把梯形问题转化为直角三角形来解决。六、作业课本第123页习题1,2,3,4七、板书设计锐角三角函数的应用(2)坡角例题做一做练习