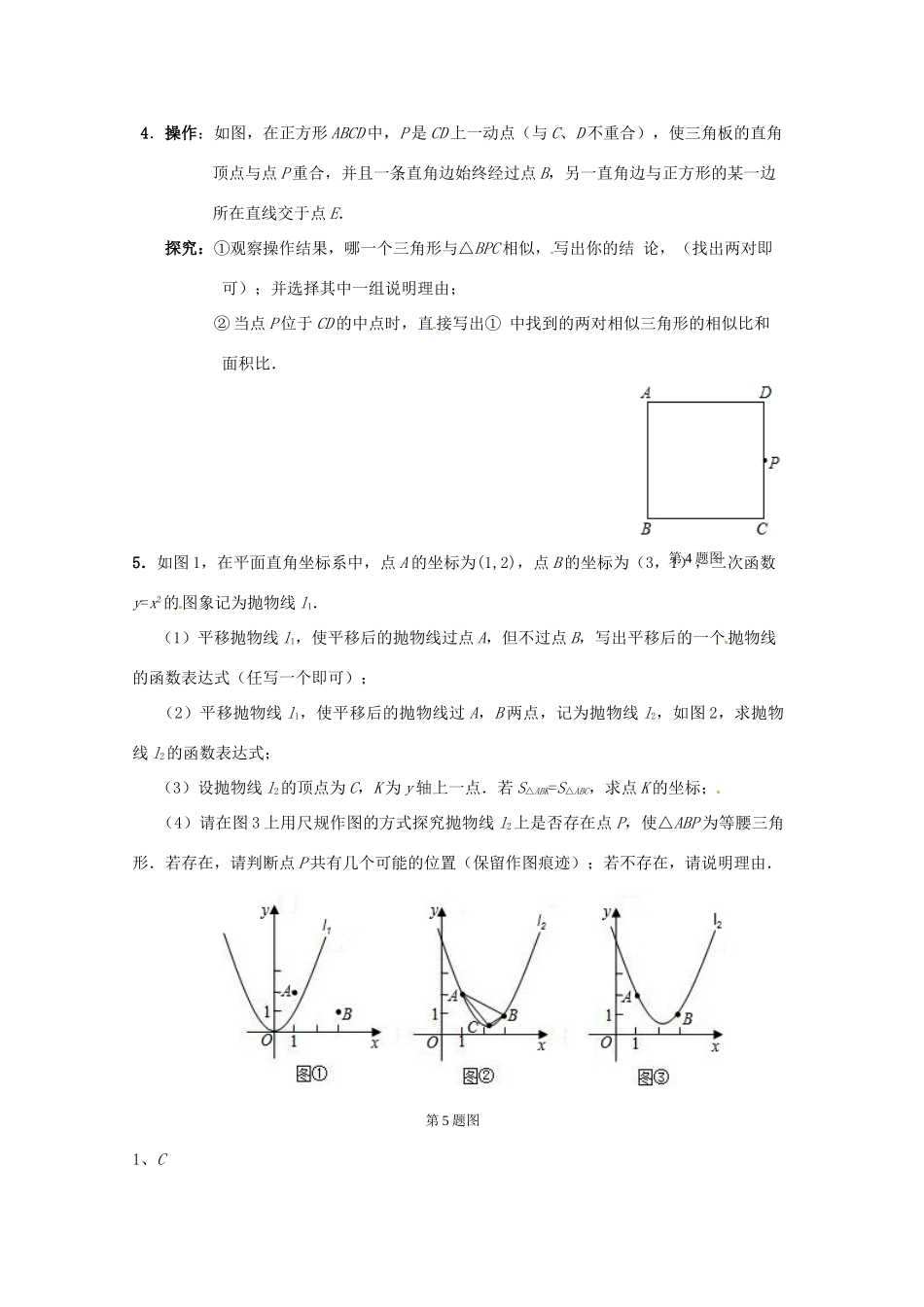
2013年九年级数学中考复习讲义系列-----每周一练(12)时间:60分钟姓名得分1.如图,将三角形纸片沿折叠,使点落在边上的点处,且∥,下列结论中,一定正确的个数是()①是等腰三角形②③四边形是菱形④A.1个B.2个C.3个D.4个2.如图,甲,乙,丙,丁四个长方形拼成正方形EFGH,中间阴影为正方形,已知,甲、乙、丙、丁四个长方形面积的和是32cm²,四边形ABCD的面积是20cm²。问甲、乙、丙、丁四个长方形周长的总和是:.第2题图3.如图1,若△ABC和△ADE为等边三角形,M,N分别为EB,CD的中点,易证:CD=BE,△AMN是等边三角形:(1)当把△ADE绕点A旋转到图2的位置时,CD=BE吗?若相等请证明,若不等于请说明理由;(2)当把△ADE绕点A旋转到图3的位置时,△AMN还是等边三角形吗?若是请证明,若不是,请说明理由(可用第一问结论).ABCDEF第1题图ACBDENMACBDENMACBDENM图1图2图3第3题图4.操作:如图,在正方形ABCD中,P是CD上一动点(与C、D不重合),使三角板的直角顶点与点P重合,并且一条直角边始终经过点B,另一直角边与正方形的某一边所在直线交于点E.探究:①观察操作结果,哪一个三角形与△BPC相似,写出你的结论,(找出两对即可);并选择其中一组说明理由;②当点P位于CD的中点时,直接写出①中找到的两对相似三角形的相似比和面积比.5.如图1,在平面直角坐标系中,点A的坐标为(1,2),点B的坐标为(3,1),二次函数y=x2的图象记为抛物线l1.(1)平移抛物线l1,使平移后的抛物线过点A,但不过点B,写出平移后的一个抛物线的函数表达式(任写一个即可);(2)平移抛物线l1,使平移后的抛物线过A,B两点,记为抛物线l2,如图2,求抛物线l2的函数表达式;(3)设抛物线l2的顶点为C,K为y轴上一点.若S△ABK=S△ABC,求点K的坐标;(4)请在图3上用尺规作图的方式探究抛物线l2上是否存在点P,使△ABP为等腰三角形.若存在,请判断点P共有几个可能的位置(保留作图痕迹);若不存在,请说明理由.1、C第5题图第4题图2、483.解:(1)CD=BE.理由如下:∵△ABC和△ADE为等边三角形∴AB=AC,AE=AD,∠BAC=∠EAD=60o∵∠BAE=∠BAC-∠EAC=60o-∠EAC,∠DAC=∠DAE-∠EAC=60o-∠EAC,∴∠BAE=∠DAC,∴△ABE≌△ACD∴CD=BE(2)△AMN是等边三角形.理由如下:∵△ABE≌△ACD,∴∠ABE=∠ACD.∵M、N分别是BE、CD的中点,∴BM=CN∵AB=AC,∠ABE=∠ACD,∴△ABM≌△ACN.∴AM=AN,∠MAB=∠NAC.∴∠NAM=∠NAC+∠CAM=∠MAB+∠CAM=∠BAC=60°∴△AMN是等边三角形.4、解:分两种情况:①如图(1),∵∠BPE=90°,∴∠BPC+∠DPE=90°,又∠BPC+∠PBC=90°,∴∠PBC=∠DPE,又∠C=∠D=90°,∴△BPC∽△PED.如图(2),同理可证△BPC∽△BEP∽△PCE.②如图(1),∵△BPC∽△PED,∴△PED与△BPC的周长比等于对应边的比,即PD与BC的比,∵点P位于CD的中点,∴PD与BC的比为1:2,∴△PED与△BPC的周长比1:2,△PED与△BPC的面积比1:4如图(2),∵△BPC∽△BEP,∴△BEP与△BPC的周长比等于对应边的比,即BP与BC的比,∵点P位于CD的中点,设BC=2k,则PC=k,BP=k,∴BP与BC的比为:2,△BEP与△BPC的周长比为:2,△BEP与△BPC的面积比为5:4.同理:△PCE∽△BPC,周长比1:2,面积比1:4.5.(1)(答案不唯一)(2)(3),(4)3个