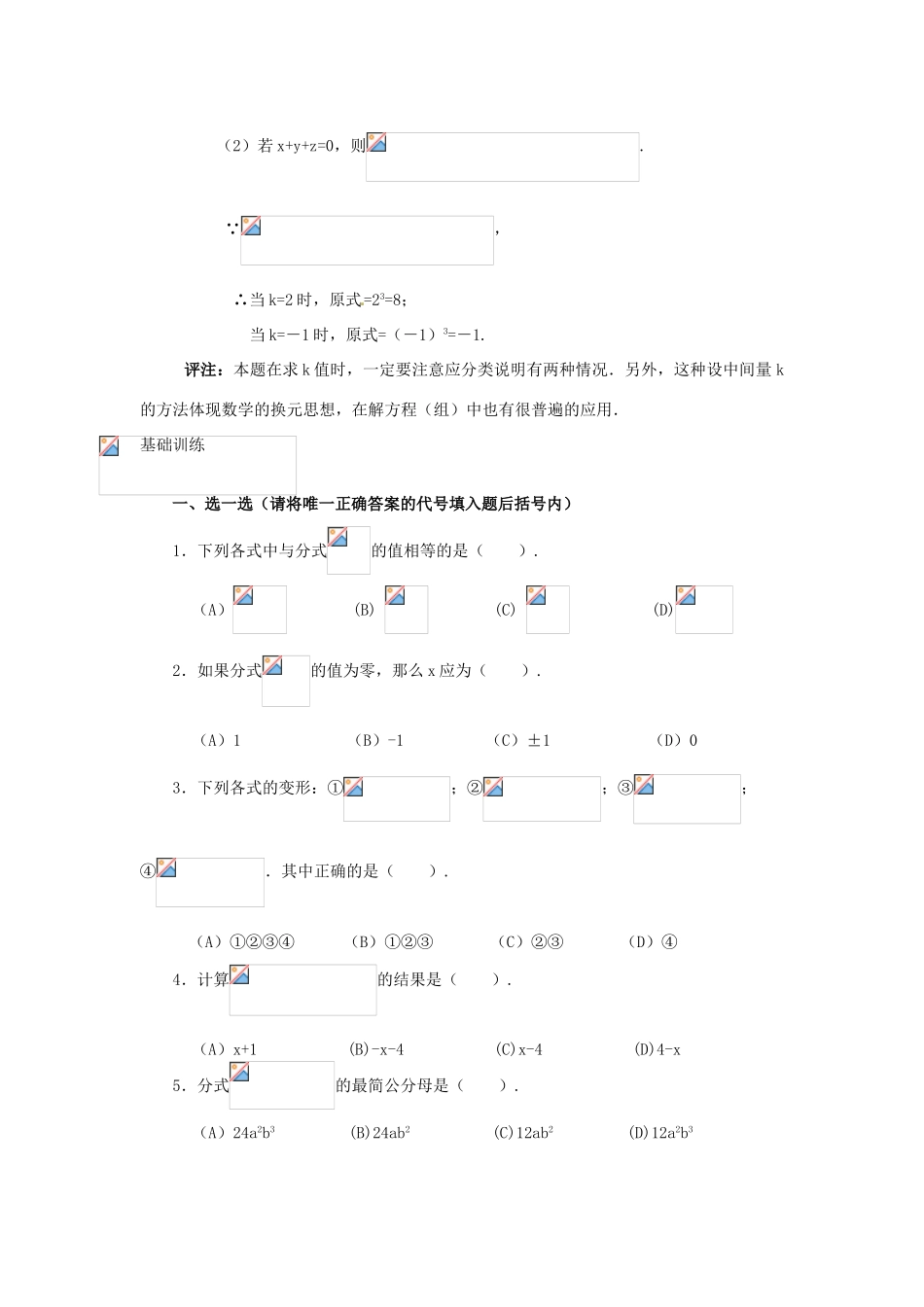
第十六章分式16.1分式疑难分析1.一般地,如果A、B表示两个整式,并且B中含有字母,那么式子叫做分式(fraction).分式的分母表示除数,由于除数不能为0,所以分式的分母不能为0,即当B≠0时,分式才有意义.2.分式的基本性质:分式的分子与分母同乘(或除以)一个不等于0的整式,分式的值不变,用式子表示的=,=(C≠0),其中A、B、C是整式,运用分式的基本性质时,千万不能忽略C≠0这一条件.3.与分数的通分类似,利用分式的基本性质,使分子和分母同乘适当的整式,不改变分式的值,这样的分式变形叫做分式的通分(changingfractionstoacommondenominator).与分数的约分类似,利用分式的基本性质,约去分子和分母的公因式,不改变分式的值,这样的分式变形叫做分式的约分(reductionofafraction).4.通分的关键是准确地找出最简公分母,找最简公分母时,从三个方面确定:(1)定系数:取各分母的系数的最小公倍数;(2)定字母:取各分母中含有的不相同字母或字母代数式的因式;(3)定指数:取相同字母或含字母的代数式的最高指数.例题选讲例1当x取何值时,下列分式有意义?(1);(2);(3).解:(1)由于分母x2+1>0,知x取任何数;(2)由分母│x│-3≠0,得x≠±3,∴当x≠±3时,分式有意义.(3)由分母x2+5x+4=(x+1)(x+4)≠0,得x≠-1且x≠-4,∴当x≠-1且x≠-4时,分式有意义.评注:在解决此类问题时,应能综合运用已学的绝对值,因式分解等知识,灵活处理,此类题型可锻炼思维的全面性.例2当x为何值时,分式的值为零?解:由题意得:,解得x=3.∴当x=3时,分式的值为零.评注:要使分式的值为零,必须使分子为零,且分母的值不为零.例3分式,若不论x取何值总有意义,则m的取值范围是().(A)m≥1(B)m>1(C)m≤1(D)m<1解:∵分母x2-2x+m=(x-1)2+m-1,∴当m-1>0,即m>1时,不论x取何实数,x2-2x+m>0,分式总有意义.∴选(B).评注:要使分式不论x取何值总有意义,只要使分母不论x取何实数总不等于零即可.例4在分式中,字母a、b的值分别扩大为原来的2倍,则分式的值().(A)扩大为原来的2倍(B)不变(C)缩小为原来的(D)缩小为原来的解:当正数a与b的值分别扩大为原来的2倍时,分子的值扩大到原来的2倍,而分母的值则扩大到原来的4倍,此时分式的值应缩小到原来的,故选(B).评注:本题考查分式的基本性质,分子乘以2,分母乘以4,所以分式的值要改变.例5若xyz≠0,且满足,求的值.解:设=k,则,∴2(x+y+z)=(x+y+z)·k.(1)若x+y+z≠0,则k=2;(2)若x+y+z=0,则.∵,∴当k=2时,原式=23=8;当k=-1时,原式=(-1)3=-1.评注:本题在求k值时,一定要注意应分类说明有两种情况.另外,这种设中间量k的方法体现数学的换元思想,在解方程(组)中也有很普遍的应用.基础训练一、选一选(请将唯一正确答案的代号填入题后括号内)1.下列各式中与分式的值相等的是().(A)(B)(C)(D)2.如果分式的值为零,那么x应为().(A)1(B)-1(C)±1(D)03.下列各式的变形:①;②;③;④.其中正确的是().(A)①②③④(B)①②③(C)②③(D)④4.计算的结果是().(A)x+1(B)-x-4(C)x-4(D)4-x5.分式的最简公分母是().(A)24a2b3(B)24ab2(C)12ab2(D)12a2b36.如果分式,那么的值为().(A)1(B)-1(C)2(D)-27.已知实数a,b满足ab-a-2b+2=0,那么的值等于().(A)(B)(C)(D)8.如果把分式中的x和y都扩大3倍,那么分式的值().(A)扩大3倍(B)不变(C)缩小3倍(D)缩小6倍二、填一填9.在代数式中,分式有个.10.当x=时,分式的值为0.11.已知,则M=.12.不改变分式的值,使分子、分母首项为正,则=.13.化简:=.14.已知有意义,且成立,则x的值不等于.15.计算:=.三、做一做16.约分(1)(2).17.通分(1)与;(2)与.18.已知,求的值.19.计算:.参考答案16.1分式一、1.C2.A3.D4.D5.C6.B7.D8.B二、9.410.111.12.13.14.-115.三、16.(1);(2)17.略18.19.