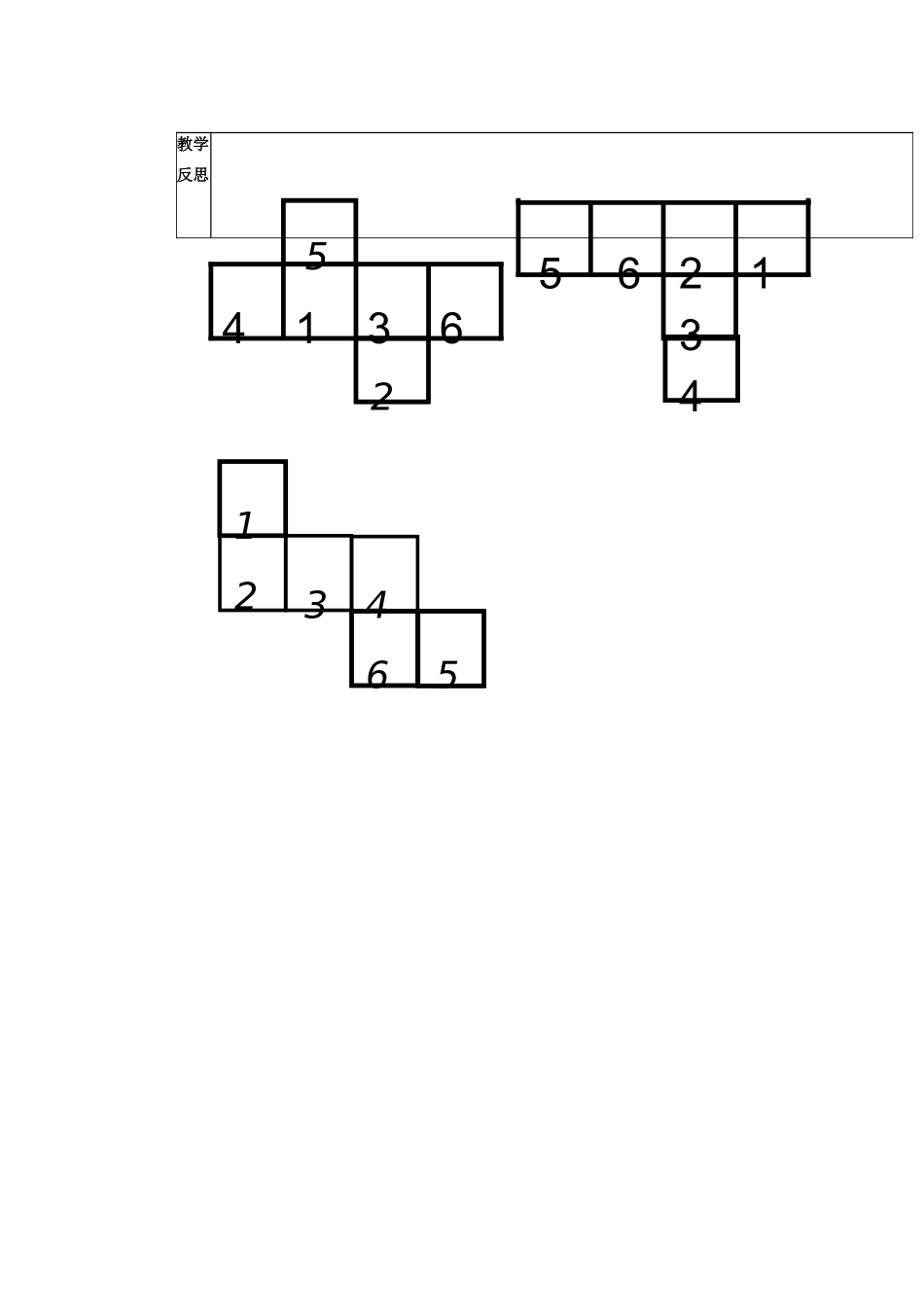
《12展开与折叠(一)》教学案课题主备人使用人审核人教学目标(一)知识与能力3、情感与态度目标:体验数学与生活的密切联系。让学生在充分经历实践、探索、交流,获得成功的体验,培养科学探索精神。(二)过程与方法(三)情感、态度与价值观教学重点将一个正方体的表面沿某些棱展开,展成平面图形;教学难点鼓励学生尽可能多地将一个正方体展成平面图形,并用语言描述其过程。教学程序集体备课内容个案补充第一环节:创设情景,导入课题在生活中,我们经常见到正方体形状的盒子.将纸盒完全展开后形状是怎样的?第二环节:动手操作、探求新知将一个正方体的表面沿某些棱剪开,能展成一个平面图形吗?你能得到哪些平面图形?与同伴进行交流.1、教师布置活动任务:请同学们将准备好的小正方体纸盒沿某条棱任意剪开,看看能得到哪些平面图形?注意强调在剪开正方体棱的过程中,正方体的6个面中每个面至少有一条棱与其它面相连。2、学生分组进行裁剪,教师巡视。并把学生剪好的平面图形贴在黑板上(重复的不再贴),可以得出11种不同的展开图:3、教师用电脑演示剪开的方法,设问:能否将得到的平面图形分类?你是按什么规律来分类的?学生讨论得出分为4类:第一类,分三排,有三种情形:中间为四个,两侧各一个,共六种;中间为三个正方形,上为两正方形,下为一正方形.此时下一正方形可以在任何位置,共三种;中间为两个正方形,上为两正方形,下为两正方形,此时只有一种情况;第二类,分两排,此时只有一种情况。从而引导学生得出一个重要结论:任何正方形组合不能是田字形。4、教师再次设问:既然都是正方体,为什么剪出的平面图形会不一样呢?学生观察手中图形,小组讨论得出同一立体图形,按不同方式展开得到的平面展开图是不一样的。当然,也有的表面上看似不同,但通过转动、翻转可得相同。5、一个正方体要将其展开成一个平面图形,必须沿几条棱剪开?学生讨论,由于正方体有12条棱,6个面,将其表面展成一个平面图形,面与面之间相连的棱有5条(即未剪开的棱),因此需要剪开7条棱。目的:使学生在动手操作的基础上,动脑思考,仔细观察这十一种展开图的特点,能够快记忆正方体的展开图。第三环节:先猜想再实践,发展几何直觉1、把一个正方体的表面沿某些棱剪开,展成一个平面图形,你能得到下面的些平面图形吗?2、下面哪一个图形经过折叠可以得到正方体?第四环节:巩固基础,检测自我4教学反思563142251436213456