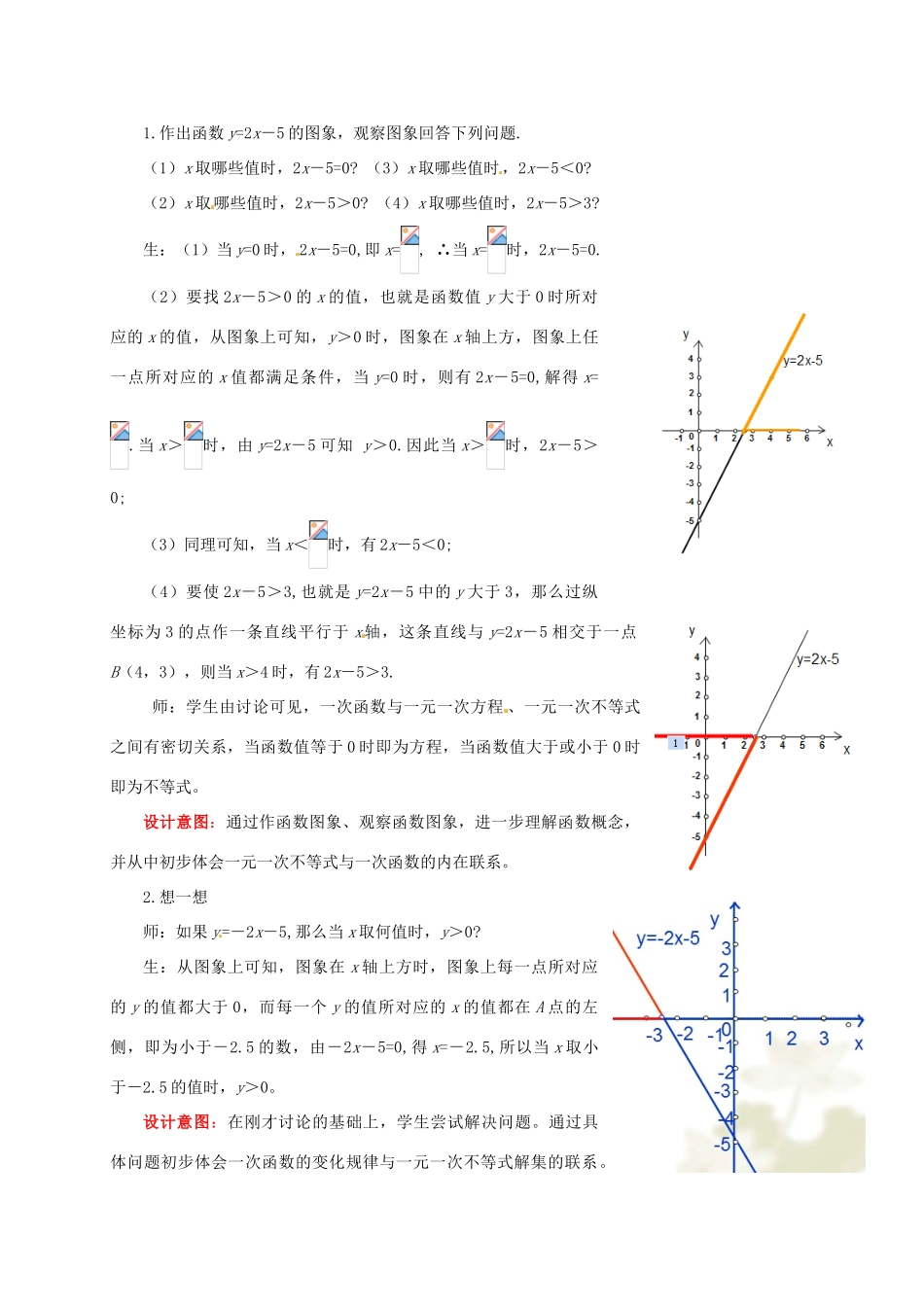
山东省枣庄市峄城区吴林街道中学八年级数学下册《第一章,一元一次不等式与一次函数(1)》教案北师大版学习目标:1、通过观察函数图象、求解方程的解和不等式的解集,从中体会一元一次方程、一元一次不等式与一次函数的内在联系.2、会根据题意列出函数关系式,画出函数图象,并利用不等关系进行比较3、通过一元一次不等式与一次函数的图象之间的结合,培养学生的数形结合意识.4、训练大家能利用数学知识去解决实际问题的能力.学习重难点:重点:(1)通过观察函数图象、求解方程的解和不等式的解集,从中体会一元一次方程、一元一次不等式与一次函数的内在联系.(2)会适当选取一元一次方程、一元一次不等式与一次函数解决实际问题.难点:会根据题意列出函数关系式,画出函数图象,并利用不等关系进行比较、一、复习回顾,引入新课师:一次函数的一般形式是什么?生:(为常数,≠0)师:如何画一次函数图象?生:两点法:、.师:我们知道一次函数与一元一次方程有着内在联系如:方程≠的解是函数与轴的交点横坐标.那么一元一次不等式与一次函数有什么联系吗?这节课我们来共同探索这个问题.设计意图:以“旧”引“新”,由原有的知识为基础,探讨新的内容。学生在回忆中探索本课时的内容,从而降低了学生们“入室”的门槛.二、活动探究,合作学习下面我们来探讨一下一元一次不等式与一次函数的图象之间的关系.1.作出函数y=2x-5的图象,观察图象回答下列问题.(1)x取哪些值时,2x-5=0?(3)x取哪些值时,2x-5<0?(2)x取哪些值时,2x-5>0?(4)x取哪些值时,2x-5>3?生:(1)当y=0时,2x-5=0,即x=,∴当x=时,2x-5=0.(2)要找2x-5>0的x的值,也就是函数值y大于0时所对应的x的值,从图象上可知,y>0时,图象在x轴上方,图象上任一点所对应的x值都满足条件,当y=0时,则有2x-5=0,解得x=.当x>时,由y=2x-5可知y>0.因此当x>时,2x-5>0;(3)同理可知,当x<时,有2x-5<0;(4)要使2x-5>3,也就是y=2x-5中的y大于3,那么过纵坐标为3的点作一条直线平行于x轴,这条直线与y=2x-5相交于一点B(4,3),则当x>4时,有2x-5>3.师:学生由讨论可见,一次函数与一元一次方程、一元一次不等式之间有密切关系,当函数值等于0时即为方程,当函数值大于或小于0时即为不等式。设计意图:通过作函数图象、观察函数图象,进一步理解函数概念,并从中初步体会一元一次不等式与一次函数的内在联系。2.想一想师:如果y=-2x-5,那么当x取何值时,y>0?生:从图象上可知,图象在x轴上方时,图象上每一点所对应的y的值都大于0,而每一个y的值所对应的x的值都在A点的左侧,即为小于-2.5的数,由-2x-5=0,得x=-2.5,所以当x取小于-2.5的值时,y>0。设计意图:在刚才讨论的基础上,学生尝试解决问题。通过具体问题初步体会一次函数的变化规律与一元一次不等式解集的联系。通过完成这题进一步培养了学生的数形结合意识。3.例题讲解兄弟俩赛跑,哥哥先让弟弟跑9m,然后自己才开始跑,已知弟弟每秒跑3m,哥哥每秒跑4m,列出函数关系式,画出函数图象,观察图象回答下列问题:(1)何时弟弟跑在哥哥前面?(2)何时哥哥跑在弟弟前面?(3)谁先跑过20m?谁先跑过100m?(4)你是怎样求解的?与同伴交流.解:设兄弟俩赛跑的时间为x秒.哥哥跑过的路程为y1,弟弟跑过的路程为y2,根据题意,得y1=4xy2=3x+9从图象上来看:生1:当0<x<9时,表示弟弟的直线y2在表示哥哥的y1上方,所以弟弟跑在哥哥前面;生2:当x>9时,y1在y2上方,所以哥哥跑在弟弟前面;生3:因为交点(9,36)表示两人到达同一地点。20<36所以弟弟先跑过20m,100>36所以哥哥先跑过100m;师:同学们说的都很好。从图象上直接可以观察出(1)、(2)小题,在第(3)题时,过y轴上20这一点作x轴的平行线,它与y1=4x,y2=3x+9分别有两个交点,每一交点都对应一个x值,哪个x的值小,说明用的时间就短.同理可知谁先跑过100m.设计意图:感知不等式、函数、方程的不同作用与内在联系.绝大部分学生都能画出函数图象,并能借助函数图象完成上述问题。三、运用巩固,练习提高1.已知y1=-x+3,y2=3x-4,当x取何值时,y1>y2?你是...