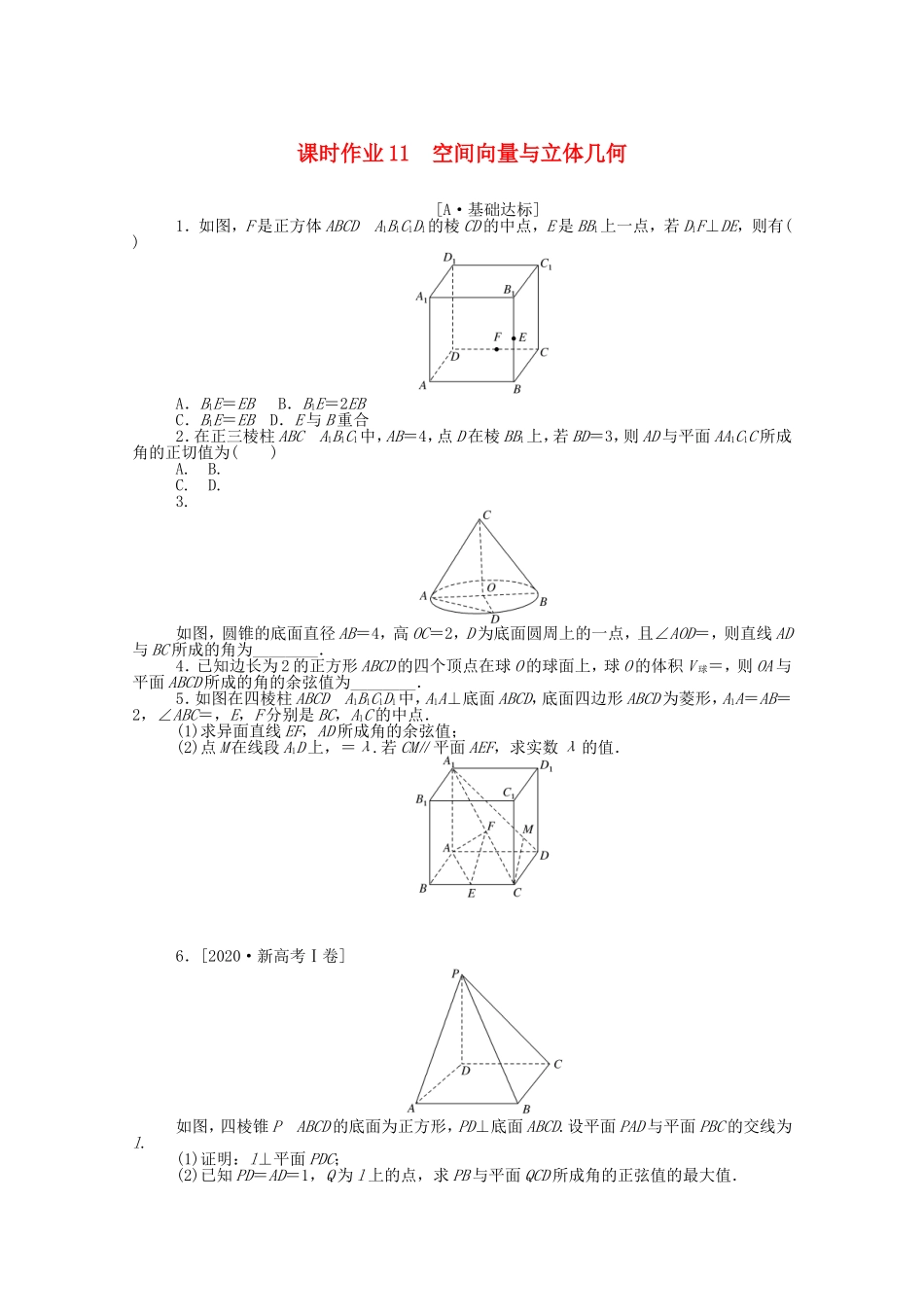
课时作业11空间向量与立体几何[A·基础达标]1.如图,F是正方体ABCDA1B1C1D1的棱CD的中点,E是BB1上一点,若D1F⊥DE,则有()A.B1E=EBB.B1E=2EBC.B1E=EBD.E与B重合2.在正三棱柱ABCA1B1C1中,AB=4,点D在棱BB1上,若BD=3,则AD与平面AA1C1C所成角的正切值为()A.B.C.D.3.如图,圆锥的底面直径AB=4,高OC=2,D为底面圆周上的一点,且∠AOD=,则直线AD与BC所成的角为________.4.已知边长为2的正方形ABCD的四个顶点在球O的球面上,球O的体积V球=,则OA与平面ABCD所成的角的余弦值为________.5.如图在四棱柱ABCDA1B1C1D1中,A1A⊥底面ABCD,底面四边形ABCD为菱形,A1A=AB=2,∠ABC=,E,F分别是BC,A1C的中点.(1)求异面直线EF,AD所成角的余弦值;(2)点M在线段A1D上,=λ.若CM∥平面AEF,求实数λ的值.6.[2020·新高考Ⅰ卷]如图,四棱锥PABCD的底面为正方形,PD⊥底面ABCD.设平面PAD与平面PBC的交线为l.(1)证明:l⊥平面PDC;(2)已知PD=AD=1,Q为l上的点,求PB与平面QCD所成角的正弦值的最大值.[B·素养提升]1.如图,在三棱柱ABCA1B1C1中,CC1⊥平面ABC,D,E,F,G分别为AA1,AC,A1C1,BB1的中点,AB=BC=,AC=AA1=2.(1)求证:AC⊥平面BEF;(2)求二面角BCDC1的余弦值;(3)证明:直线FG与平面BCD相交.2.如图,在三棱柱ABCDEF中,所有棱长均相等,且∠ABE=∠ACF=,CE∩BF=O,点P为线段ED上的动点(异于E,D两点).(1)当P在线段ED的中点时,证明:OP∥平面ACFD;(2)当P在线段ED上何处时,二面角OPFE的余弦值为?3.在▱PABC中,PA=4,PC=2,∠P=45°,D是PA的中点(如图1).将△PCD沿CD折起到图2中△P1CD的位置,得到四棱锥P1ABCD.(1)将△PCD沿CD折起的过程中,CD⊥平面P1DA是否成立?请证明你的结论.(2)若P1D与平面ABCD所成的角为60°,且△P1DA为锐角三角形,求平面P1AD和平面P1BC所成角的余弦值.课时作业11空间向量与立体几何[A·基础达标]1.解析:分别以DA,DC,DD1所在直线为x,y,z轴建立空间直角坐标系,设正方体的棱长为2,则D(0,0,0),F(0,1,0),D1(0,0,2),设E(2,2,z),则D1F=(0,1,-2),DE=(2,2,z),因为D1F·DE=0×2+1×2-2z=0,所以z=1,所以B1E=EB.答案:A2.解析:如图,可得AD·EB=(AB+BD)·EB=AB·EB=4×2×=12=5×2×cosθ(θ为AD与EB的夹角),所以cosθ=,sinθ=,tanθ=,又因为BE⊥平面AA1C1C,所以所求角的正切值为.答案:D3.解析:如图,过点O作OE⊥AB交底面圆于E,分别以OE,OB,OC所在直线为x,y,z轴建立空间直角坐标系,因为∠AOD=π,所以∠BOD=,则D(,1,0),A(0,-2,0),B(0,2,0),C(0,0,2),AD=(,3,0),BC=(0,-2,2),所以cos〈AD,BC〉=-=-,则直线AD与BC所成的角为.答案:4.解析:如图,过点O作OM⊥平面ABCD,垂足为点M,则点M为正方形ABCD的中心. 正方形ABCD的边长为2,∴AC=2,∴AM=. V球=πr3=,∴球O的半径OA=r=2,∴OA与平面ABCD所成的角的余弦值为cos∠OAM===.答案:5.解析:(1)因为由题意知四棱柱ABCDA1B1C1D1为直四棱柱,A1A⊥平面ABCD.又AE⊂平面ABCD,AD⊂平面ABCD,所以A1A⊥AE,A1A⊥AD.在菱形ABCD中,∠ABC=,则△ABC是等边三角形.因为点E是BC中点,所以BC⊥AE.因为BC∥AD,所以AE⊥AD.故建立如图所示,以A为原点,AE为x轴,AD为y轴,AA1为z轴的空间直角坐标系Axyz,则A(0,0,0),C(,1,0),D(0,2,0),A1(0,0,2),E(,0,0),F.AD=(0,2,0),EF=,cos〈AD,EF〉===,所以异面直线EF,AD所成角的余弦值为.(2)设M(x,y,z),由于点M在线段A1D上,且=λ,则(x,y,z-2)=λ(0,2,-2).则M(0,2λ,2-2λ),CM=(-,2λ-1,2-2λ).设平面AEF的一个法向量为n=(x0,y0,z0).因为AE=(,0,0),AF=.由得x0=0,y0+z0=0,取y0=2,则z0=-1,则平面AEF的一个法向量为n=(0,2,-1).由于CM∥平面AEF,则n·CM=0,即2(2λ-1)-(2-2λ)=0,解得λ=.6.解析:(1)因为PD⊥底面ABCD,所以PD⊥AD.又底面ABCD为正方形,所以AD⊥DC.因此AD⊥平面PDC.因为AD∥BC,AD⊄平面PBC,所以AD∥平面PBC.由已知得l∥AD.因此l⊥平面PDC.(2)以D为坐标原点,DA...