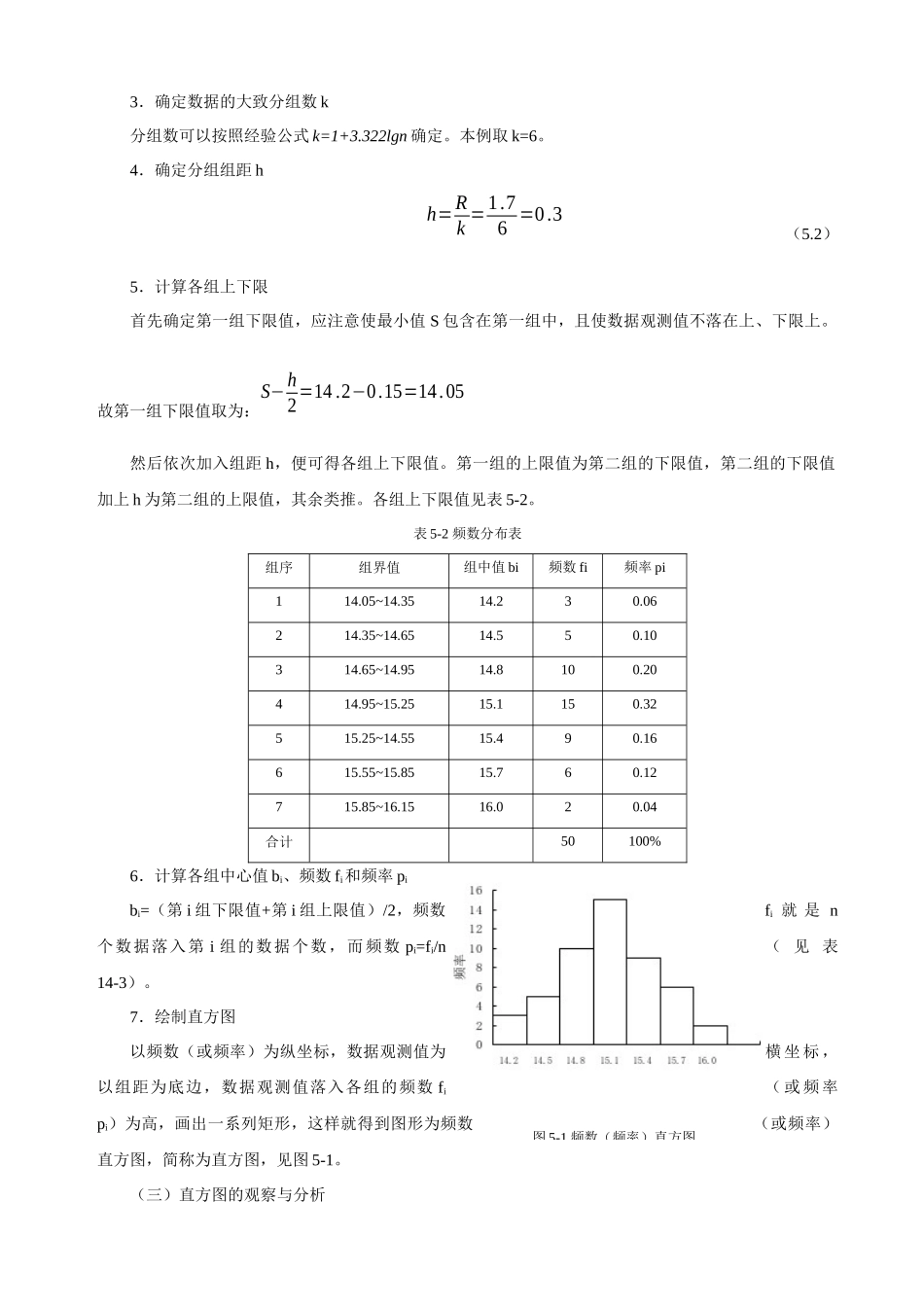
过程质量控制技术自1924年,休哈特提出控制图以来,经过近80世纪的发展,过程质量控制技术已经广泛地应用到质量管理中,在实践中也不断地产生了许多种新的方法。如直方图、相关图、排列图、控制图和因果图等“QC七种工具”以及关联图、系统图等“新QC七种工具”。应用这些方法可以从经常变化的生产过程中,系统地收集与产品有关的各种数据,并用统计方法对数据进行整理、加工和分析,进而画出各种图表,找出质量变化的规律,实现对质量的控制。石川謦曾经说过,企业内95%的质量问题可通过企业全体人员应用这些工具得到解决。无论是ISO9000还是近年来非常风行的6Sigma质量管理理论都非常强调这些基于统计学的质量控制技术的应用。因此,要真正提高产品质量,企业上至领导下至员工都必须掌握质量控制技术并在实践中加以应用。一直方图(一)直方图用途直方图法是把数据的离散状态分布用竖条在图表上标出,以帮助人们根据显示出的图样变化,在缩小的范围内寻找出现问题的区域,从中得知数据平均水平偏差并判断总体质量分布情况。(二)直方图画法下面通过例子介绍直方图如何绘制。[例5-1]生产某种滚珠,要求直径x为15.0±1.0mm,试用直方图对生产过程进行统计分析。1.收集数据在5M1E(人、机、法、测量和生产环境)充分固定并加以标准化的情况下,从该生产过程收集n个数据。N应不小于50,最好在100以上。本例测得50个滚珠的直径如下表。其中Li为第i行数据最大值,Si为第i行数据最小值。表5-150个滚珠样本直径JI12345678910LiSi115.015.815.215.115.914.714.815.515.615.315.914.7215.115.315.015.615.714.814.514.214.914.915.714.2315.215.015.315.615.114.914.214.615.815.215.814.2415.915.215.014.914.814.515.115.515.515.515.914.5515.115.015.314.714.515.515.014.714.614.215.514.22.找出数据中最大值L、最小值S和极差RL=MaxLi=15.9,S=MinSi=14.2,R=S-L=1.7(5.1)区间[S,L]称为数据的散布范围。3.确定数据的大致分组数k分组数可以按照经验公式k=1+3.322lgn确定。本例取k=6。4.确定分组组距hh=Rk=1.76=0.3(5.2)5.计算各组上下限首先确定第一组下限值,应注意使最小值S包含在第一组中,且使数据观测值不落在上、下限上。故第一组下限值取为:S−h2=14.2−0.15=14.05然后依次加入组距h,便可得各组上下限值。第一组的上限值为第二组的下限值,第二组的下限值加上h为第二组的上限值,其余类推。各组上下限值见表5-2。表5-2频数分布表组序组界值组中值bi频数fi频率pi114.05~14.3514.230.06214.35~14.6514.550.10314.65~14.9514.8100.20414.95~15.2515.1150.32515.25~14.5515.490.16615.55~15.8515.760.12715.85~16.1516.020.04合计50100%6.计算各组中心值bi、频数fi和频率pibi=(第i组下限值+第i组上限值)/2,频数fi就是n个数据落入第i组的数据个数,而频数pi=fi/n(见表14-3)。7.绘制直方图以频数(或频率)为纵坐标,数据观测值为横坐标,以组距为底边,数据观测值落入各组的频数fi(或频率pi)为高,画出一系列矩形,这样就得到图形为频数(或频率)直方图,简称为直方图,见图5-1。(三)直方图的观察与分析图5-1频数(频率)直方图从直方图可以直观地看出产品质量特性的分布形态,便于判断过程是否出于控制状态,以决定是否采取相应对策措施。直方图从分布类型上来说,可以分为正常型和异常型。正常型是指整体形状左右对称的图形,此时过程处于稳定(统计控制状态)。如图5-2a。如果是异常型,就要分析原因,加以处理。常见的异常型主要有六种:1.双峰型(图5-2b):直方图出现两个峰。主要原因是观测值来自两个总体,两个分布的数据混合在一起造成的,此时数据应加以分层。2.锯齿型(图5-2c):直方图呈现凹凸不平现象。这是由于作直方图时数据分组太多,测量仪器误差过大或观测数据不准确等造成的。此时应重新收集和整理数据。3.陡壁型(图5-2d):直方图像峭壁一样向一边倾斜。主要原因是进行全数检查,使用了剔除了不合格品的产品数据作直方图。4.偏态型:(图5-2e):直方图的顶峰偏向左侧或右侧。当公差下限受到限制(如单侧形位公差)或某种加工习...