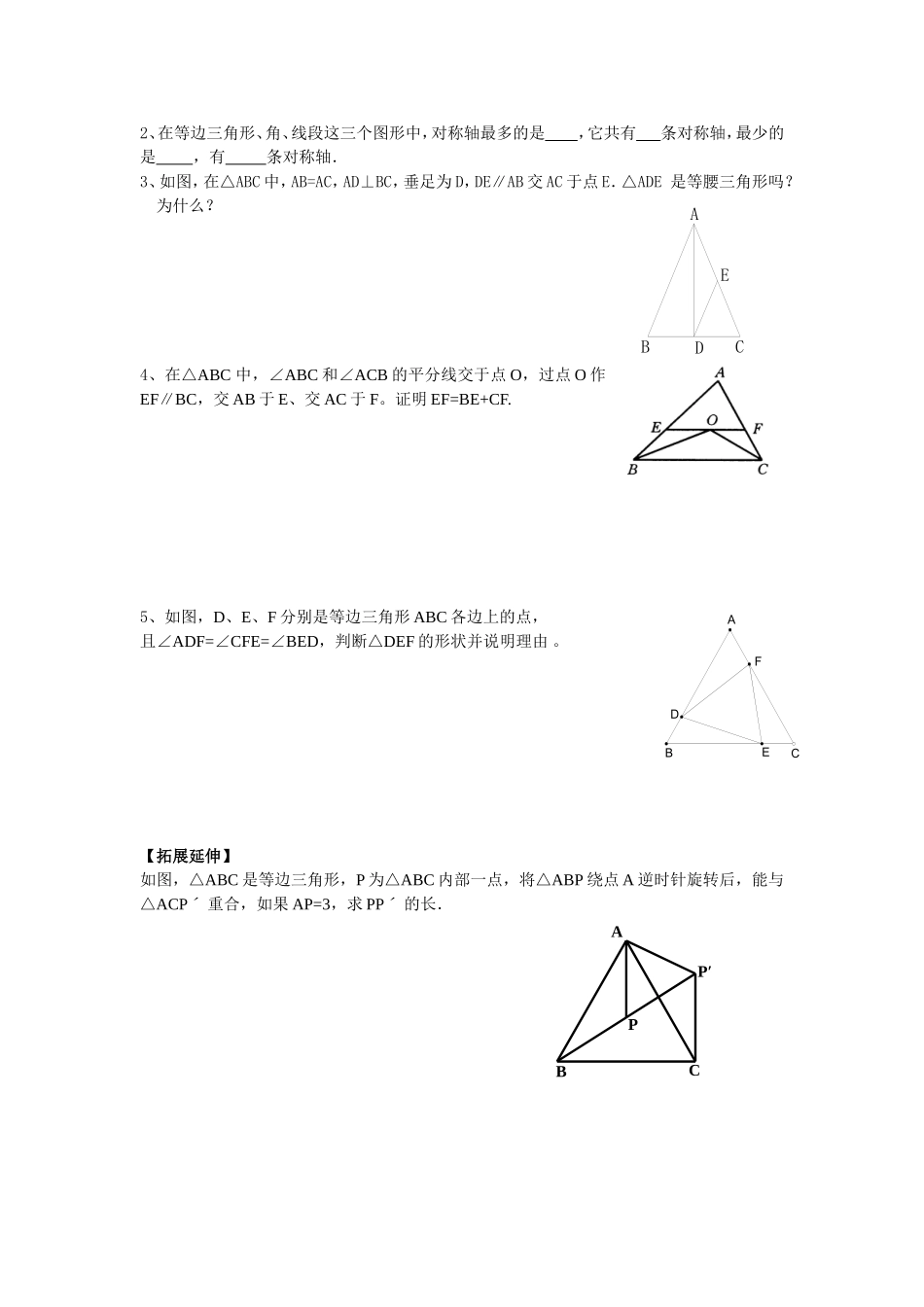
AB212.5等腰三角形的轴对称性(2)备课人:王秀琴教学目标:1知识与技能:掌握等角对等边的性质,能用等边三角形的性质及判定进行计算和说理。2过程与方法:经历“折纸、画图、观察、归纳”的活动过程,发展学生的空间观念和抽象概括能力,感受分类、转化等数学思想方法。3情感、态度与价值观:进一步发展有条理的思考和表达,提高演绎推理的能力。教学重点:等角对等边的性质,等边三角形的性质及判定。教学难点:等角对等边的性质,等边三角形的性质及判定的应用。教学过程:一、自主学习1.在一个三角形中,如果有两条边相等,那么这两条边所对的角。反过来,在一个三角形中,如果有两个角相等,那么这两个角所对的边的大小有什么关系呢?2.探索发现(1)将一张长方形的纸条上任意画出一条截线AB,所得的∠1与∠2相等吗?为什么?经过折叠后所得的△ABC,在所得的三角形中∠1=∠2。度量边AC,BC的长度,有什么发现?发现了。这是不是巧合呢?已知:△∠ABC,∠B=∠C。证明:AB=AC。得到等腰三角形判定定理:。(2)三边相等的三角形叫做等边三角形或正三角形。问题1:等腰三角形具有哪些性质?问题2:当等腰三角形的底边与腰相等时是等边三角形,它有哪些性质?等边三角形是图形,有条对称轴。等边三角形的内角都,且都等于°。等边三角形各边上和所对角的平分线都三线合一。得到等边三角形性质定理:。问题2:如何判定一个三角形是等边三角形?3个角相等的三角形是等边三角形吗?为什么?有一个角等于的等腰三角形是等边三角形吗?为什么?得到等边三角形判定定理:。。二、知识运用例1.如图,在△ABC中,AB=AC,角平分线BD、CE相交于点O,OB与OC相等吗?请说明理由.BAC2121ODECBACDEBA例2.如图,D、E、F分别是等边三角形ABC各边上的点,且AD=BE=CF,判断△DEF的形状并说明理由。三、当堂训练1.在△ABC中,已知点E在BA的延长线上,并且∠1=∠2,AD∥BC.△ABC是什么三角形?为什么?2.如图,在△ABC中,AB=AC,∠BAC=120°,AD⊥AB,AE⊥AC.⑴图中,等于30°的角有___,等于60°的角有;⑵△ADE是等边三角形吗?为什么?⑶在Rt△ABD中,∠B=_____,AD=_____BD;在Rt△ACE中,有类似结论吗?四、自我总结《2.5等腰三角形的轴对称性(2)》课后作业【基础演练】姓名________日期________得分________1、△ABC中,∠A=30°,当∠B=_______时,△ABC是等腰三角形.E2DCBA1FEDCBAEDCBAABCP′P2、在等边三角形、角、线段这三个图形中,对称轴最多的是,它共有条对称轴,最少的是,有条对称轴.3、如图,在△ABC中,AB=AC,AD⊥BC,垂足为D,DE∥AB交AC于点E.△ADE是等腰三角形吗?为什么?4、在△ABC中,∠ABC和∠ACB的平分线交于点O,过点O作EF∥BC,交AB于E、交AC于F。证明EF=BE+CF.5、如图,D、E、F分别是等边三角形ABC各边上的点,且∠ADF=∠CFE=∠BED,判断△DEF的形状并说明理由。【拓展延伸】如图,△ABC是等边三角形,P为△ABC内部一点,将△ABP绕点A逆时针旋转后,能与△ACPˊ重合,如果AP=3,求PPˊ的长.FEDCBA