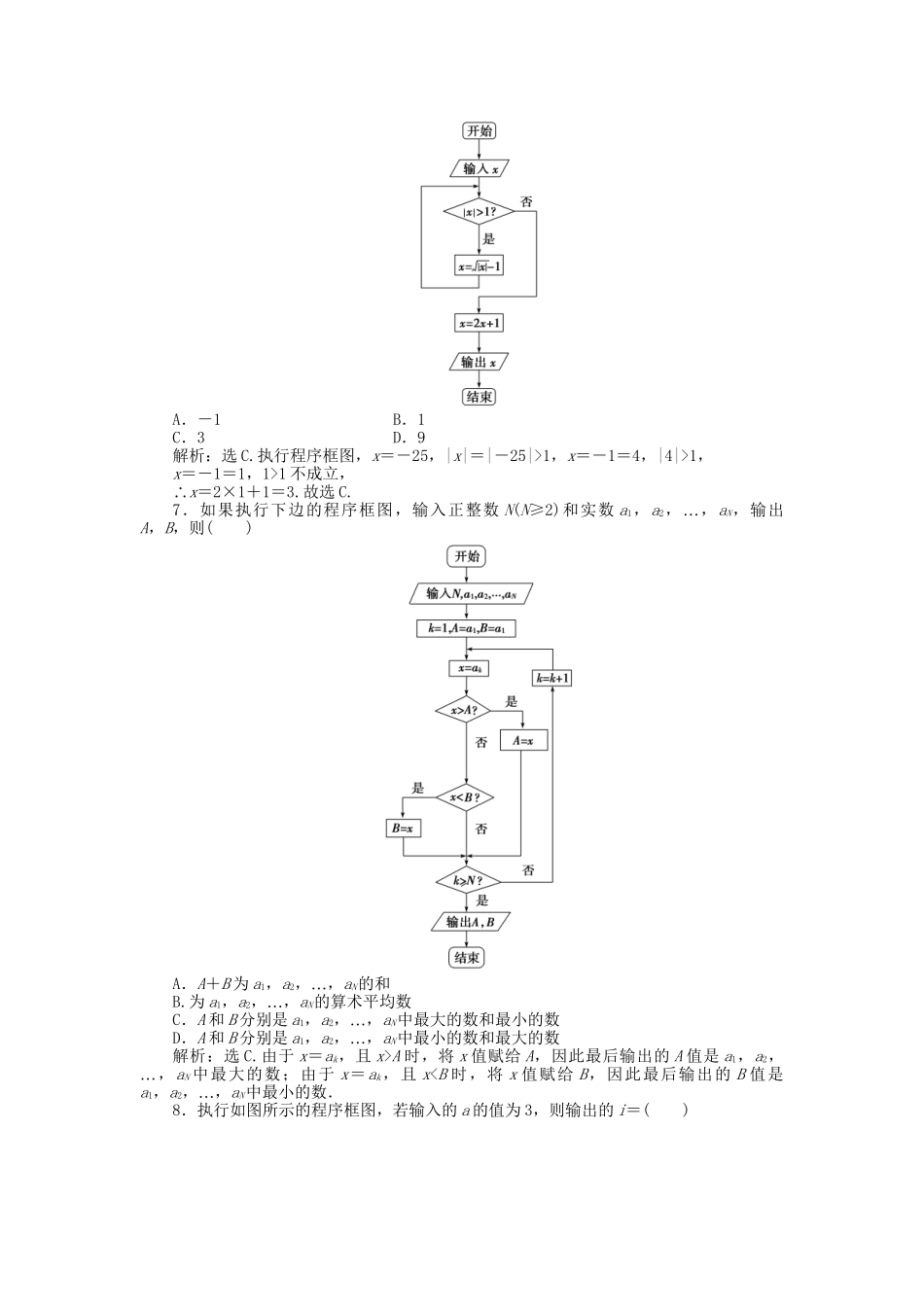
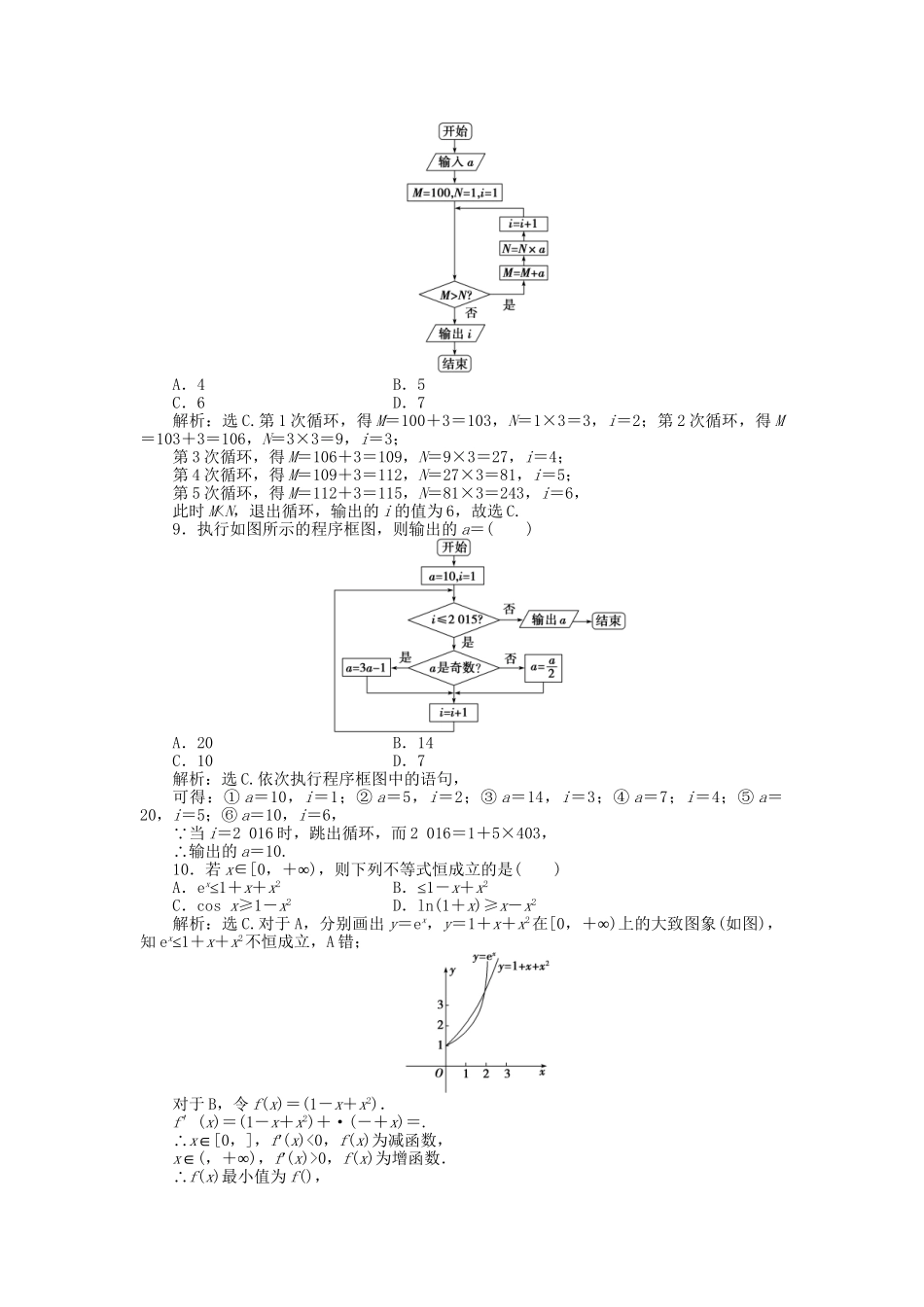
(通用版)2016年高考数学二轮复习专题十二推理与证明、算法初步专题强化训练理(时间:45分钟满分:60分)一、选择题1.观察下列各式:a+b=1,a2+b2=3,a3+b3=4,a4+b4=7,a5+b5=11…,,则a10+b10=()A.28B.76C.123D.199解析:选C.法一:由a+b=1,a2+b2=3,得ab=-1,代入三个等式中均符合,则a10+b10=(a5+b5)2-2a5b5=123,故选C.法二:令an=an+bn,则a1=1,a2=3,a3=4,a4=7,…得an+2=an+an+1,从而a6=18,a7=29,a8=47,a9=76,a10=123,故选C.2.观察下列各式:55=3125,56=15625,57=78125…,,则52016的末四位数字为()A.3125B.5625C.0625D.8125解析:选C.55=3125,56=15625,57=78125,58=390625,59=1953125,…,可得59与55的后四位数字相同,由此可归纳出5m+4k与5m(k∈N*,m=5,6,7,8)的后四位数字相同,又2016=4×502+8,所以52016与58后四位数字相同为0625,故选C.3.设f(x)=,利用推导等差数列前n——项和的方法倒序相加法,得到f(-5)+f(-4)…++f(0)…++f(5)+f(6)的值为()A.3B.C.3D.2解析:选A.f(x)+f(1-x)=+=.设S=f(-5)+f(-4)…++f(0)…++f(5)+f(6),又S=f(6)+f(5)…++f(0)…++f(-4)+f(-5),∴2S=12[f(-5)+f(6)]=,∴S=3.4.用数学归纳法证明12+22…++(n-1)2+n2+(n-1)2…++22+12=时,由n=k的假设到证明n=k+1时,等式左边应添加的式子是()A.(k+1)2+2k2B.(k+1)2+k2C.(k+1)2D.(k+1)[2(k+1)2+1]解析:选B.本题易被题干误导而错选A,分析等式变化规律可知左边实际增加的是(k+1)2+k2.5.已知a,b,μ∈(0,∞+),且+=1,则使得a+b≥μ恒成立的μ的最大值为()A.8B.9C.16D.25解析:选C. a,b∈(0,∞+)且+=1,∴a+b=(a+b)(+)=10+(+)≥10+2=16,要使a+b≥μ恒成立,需16≥μ,故μ的最大值为16.6.阅读下边的程序框图,运行相应的程序,当输入x的值为-25时,输出x的值为()A.-1B.1C.3D.9解析:选C.执行程序框图,x=-25,|x|=|-25|>1,x=-1=4,|4|>1,x=-1=1,1>1不成立,∴x=2×1+1=3.故选C.7.如果执行下边的程序框图,输入正整数N(N≥2)和实数a1,a2…,,aN,输出A,B,则()A.A+B为a1,a2…,,aN的和B.为a1,a2…,,aN的算术平均数C.A和B分别是a1,a2…,,aN中最大的数和最小的数D.A和B分别是a1,a2…,,aN中最小的数和最大的数解析:选C.由于x=ak,且x>A时,将x值赋给A,因此最后输出的A值是a1,a2,…,aN中最大的数;由于x=ak,且x0,f(x)为增函数.∴f(x)最小值为f(),f()=×[1-×+×()2]=×=<1,B错;对于C,结合图象(如图)知正确;对于D,当x=4时,ln5