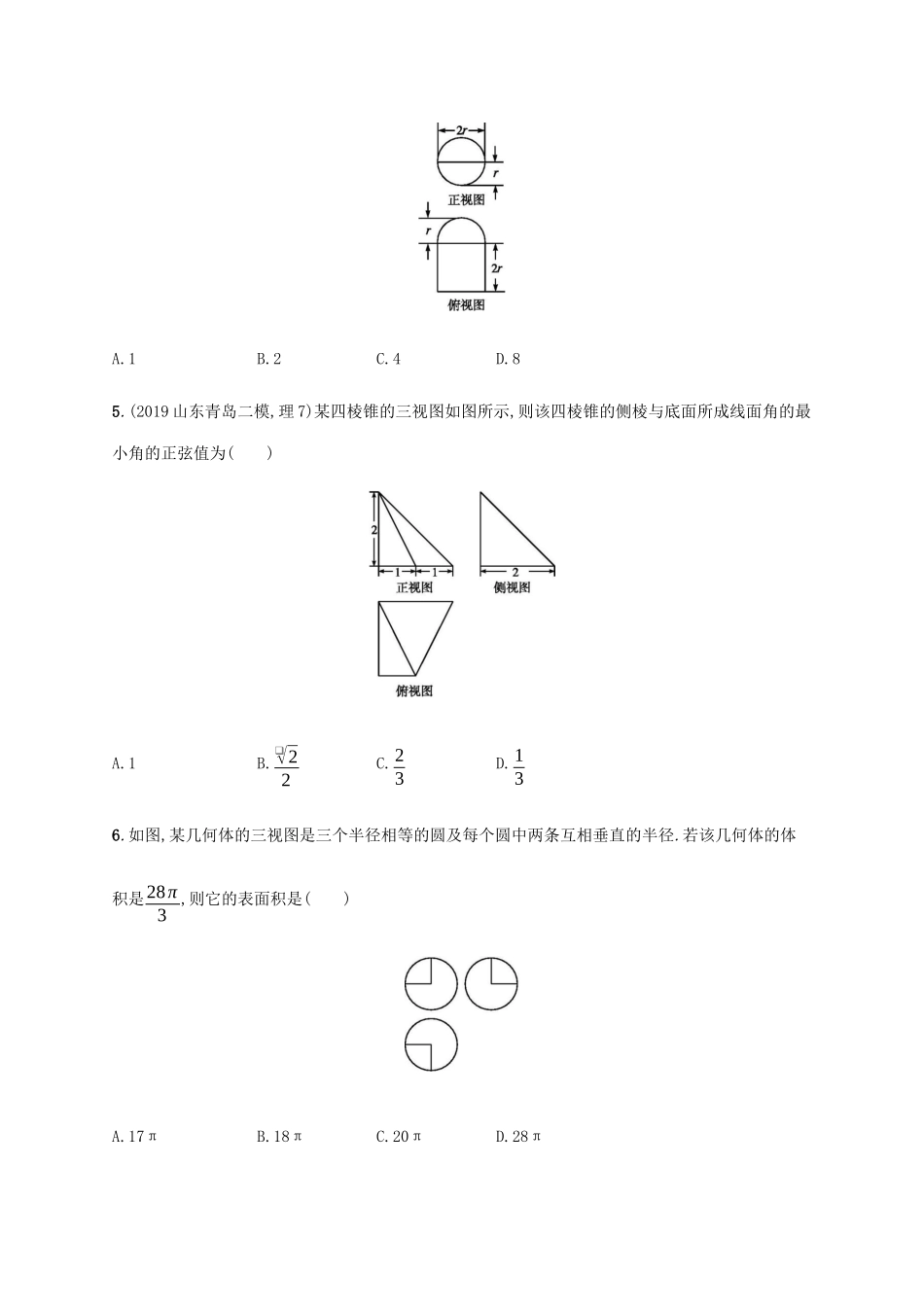
专题突破练19专题五立体几何过关检测一、选择题1.(2019天津实中模拟六,理4)若l,m是两条不同的直线,m⊥平面α,则“l⊥m”是“l∥α”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件2.一个正方体被一个平面截去一部分后,剩余部分的三视图如下图,则截去部分体积与剩余部分体积的比值为()A.18B.17C.16D.153.已知m,n为异面直线,m⊥平面α,n⊥平面β.直线l满足l⊥m,l⊥n,l⊄α,l⊄β,则()A.α∥β且l∥αB.α⊥β且l⊥βC.α与β相交,且交线垂直于lD.α与β相交,且交线平行于l4.圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示.若该几何体的表面积为16+20π,则r=()A.1B.2C.4D.85.(2019山东青岛二模,理7)某四棱锥的三视图如图所示,则该四棱锥的侧棱与底面所成线面角的最小角的正弦值为()A.1B.❑√22C.23D.136.如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是28π3,则它的表面积是()A.17πB.18πC.20πD.28π7.(2019山东聊城一模,理7)如图,圆柱的轴截面为正方形ABCD,E为弧BC的中点,则异面直线AE与BC所成角的余弦值为()A.❑√33B.❑√55C.❑√306D.❑√668.在封闭的直三棱柱ABC-A1B1C1内有一个体积为V的球.若AB⊥BC,AB=6,BC=8,AA1=3,则V的最大值是()A.4πB.9π2C.6πD.32π39.(2019河北衡水同卷联考,理10)在边长为8的等边三角形ABC中,D,E分别为AC,AB的中点,现将△ADE沿DE折起到△A'DE的位置,使得A'B=2❑√10,则直线A'B与底面BCDE所成角的正弦值为()A.❑√1010B.❑√3010C.❑√7010D.❑√21710.(2019河南名校联盟压轴卷四,理10)一个圆锥的母线长为2,圆锥的母线与底面的夹角为π4,圆锥内有一个内接正方体,则这个正方体的体积为()A.2(❑√2-1)B.8(2-❑√2)3C.8(❑√2-1)3D.8(❑√2+1)311.(2019新疆乌鲁木齐二模,理11)已知A,B,C为球O的球面上的三个定点,∠ABC=60°,AC=2,P为球O的球面上的动点,记三棱锥P-ABC的体积为V1,三棱锥O-ABC的体积为V2,若V1V2的最大值为3,则球O的表面积为()A.16π9B.64π9C.3π2D.6π12.(2019北京师大附中模拟三,理8)已知在长方体ABCD-A1B1C1D1中,B1C与C1D所成角的余弦值为❑√64,B1C与底面ABCD所成角的正弦值为❑√32,则C1D与底面ABCD所成角的余弦值为()A.12B.❑√22C.❑√63D.❑√32二、填空题13.α,β是两个平面,m,n是两条直线,有下列四个命题:①如果m⊥n,m⊥α,n∥β,那么α⊥β.②如果m⊥α,n∥α,那么m⊥n.③如果α∥β,m⊂α,那么m∥β.④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.其中正确的命题有.(填写所有正确命题的编号)14.(2019天津卷,理11)已知四棱锥的底面是边长为❑√2的正方形,侧棱长均为❑√5.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点,另一个底面的圆心为四棱锥底面的中心,则该圆柱的体积为.15.在三棱锥D-ABC中,CD⊥底面ABC,AC⊥BC,AB=BD=5,BC=4,则此三棱锥的外接球的表面积为.16.(2019北京师大附中模拟三,理13)某工厂现将一棱长为❑√3的正四面体毛坯件切割成一个圆柱体零件,则该圆柱体体积的最大值为.三、解答题17.(2019江苏卷,16)如图,在直三棱柱ABC-A1B1C1中,D,E分别为BC,AC的中点,AB=BC.求证:(1)A1B1∥平面DEC1;(2)BE⊥C1E.18.(2019四川成都二模,理19)如图①,在等腰梯形ABCD中,AB∥CD,E,F分别为AB,CD的中点,CD=2AB=2EF=4,M为DF中点.现将四边形BEFC沿EF折起,使平面BEFC⊥平面AEFD,得到如图②所示的多面体.在图②中,(1)证明:EF⊥MC;(2)求二面角M-AB-D的余弦值.19.(2019山东济宁一模,理18)如图,在四棱锥P-ABCD中,底面ABCD为平行四边形,PA⊥底面ABCD,∠ABC=60°,AB=❑√3,AD=2❑√3,AP=3.(1)求证:平面PCA⊥平面PCD;(2)设E为侧棱PC上的一点,若直线BE与底面ABCD所成的角为45°,求二面角E-AB-D的余弦值.20.(2019北京卷,理16)如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD⊥CD,AD∥BC,PA=AD=CD=2,BC=3.E为PD的中点,点F在PC上,且PFPC=13.(1)求证:CD⊥平面PAD;(2)求二面角F-AE-P的余弦值;(3)设点G在PB上,且PGPB=23,判断直线AG是否在平面AEF内,说明理由.21.(2019天津卷,理17)如图,AE⊥平面ABCD,CF∥AE,AD∥BC,AD⊥AB,A...