2022年中考数学几何模型之一线三垂直模型讲+练原卷版VIP免费

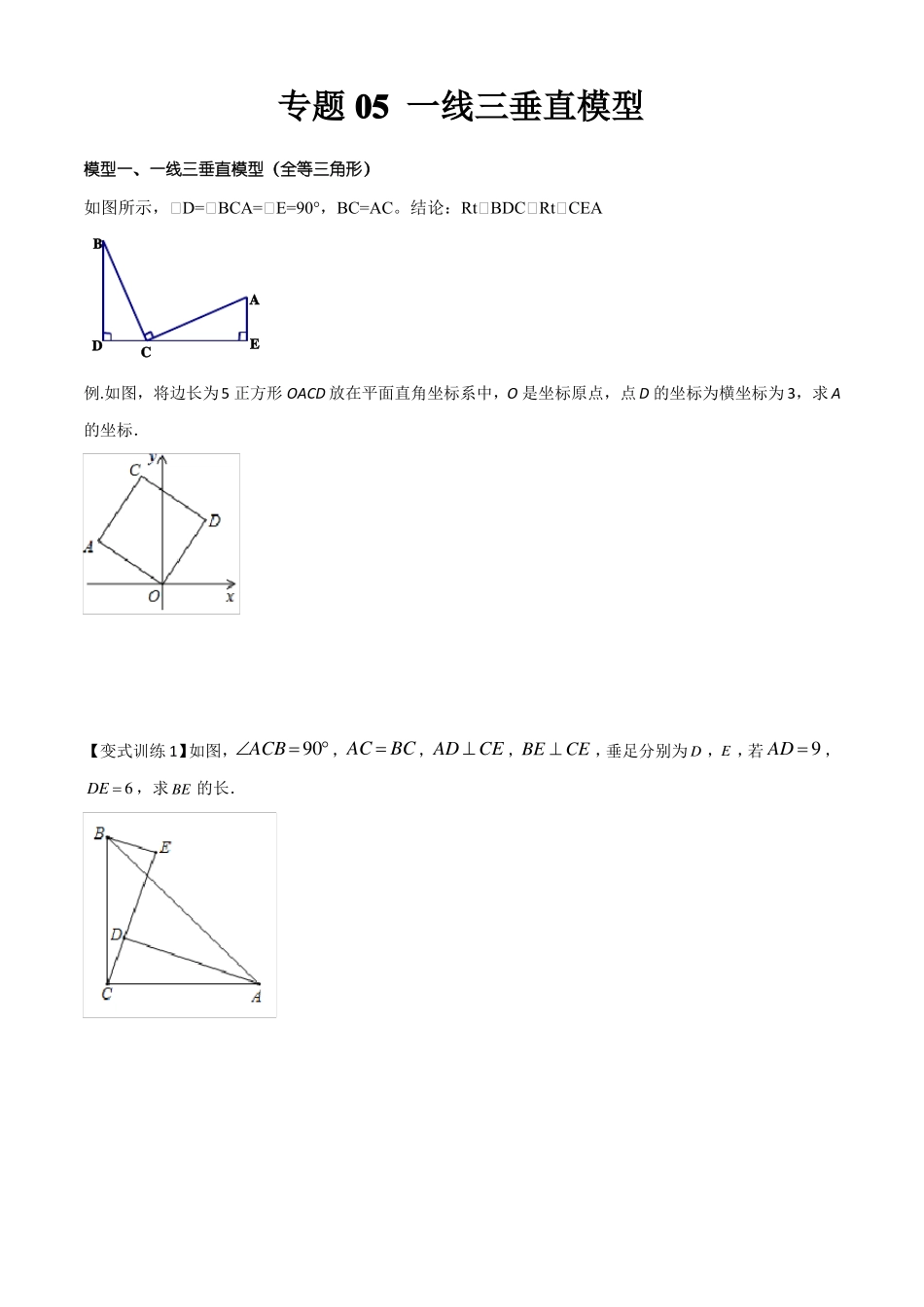
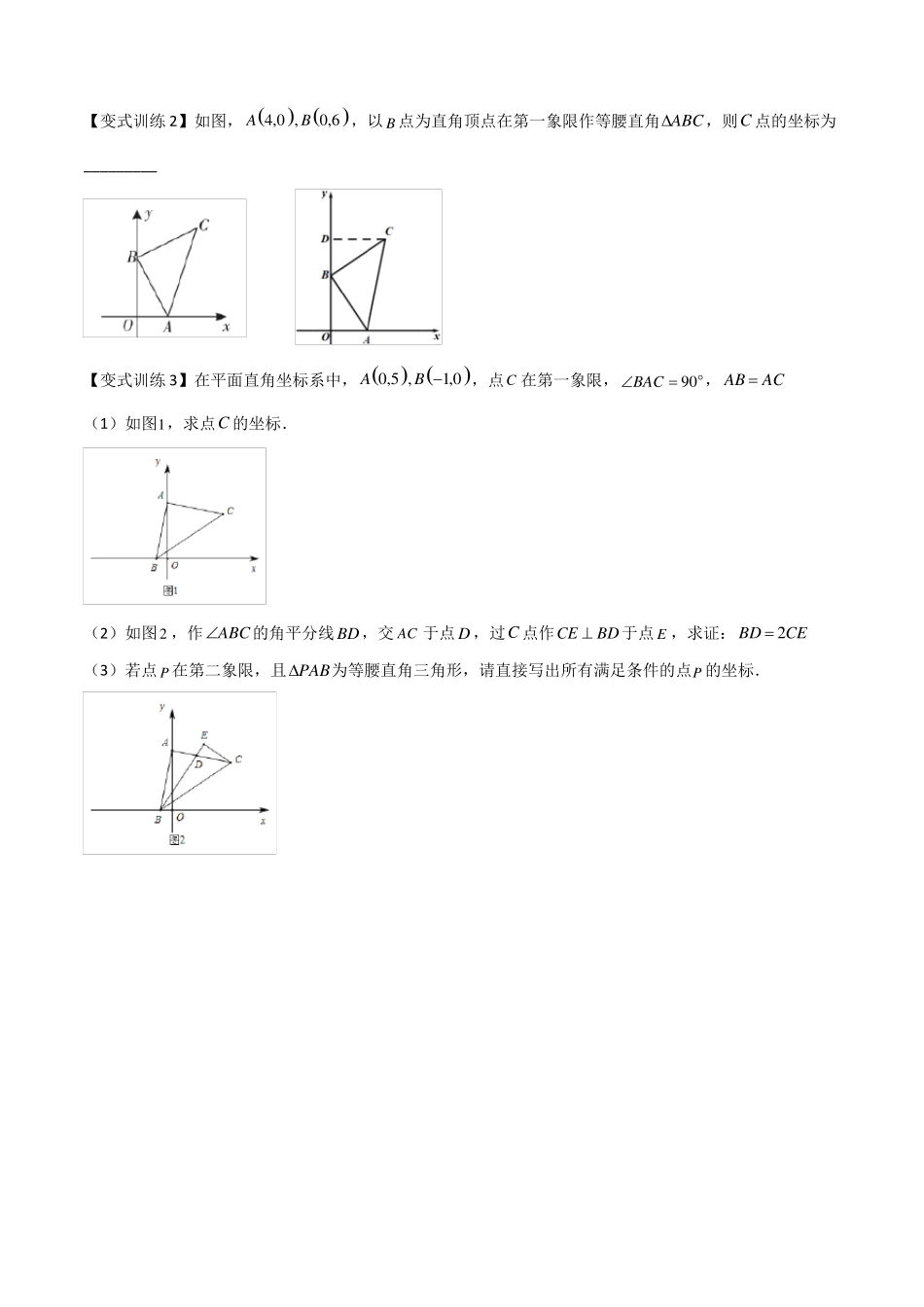
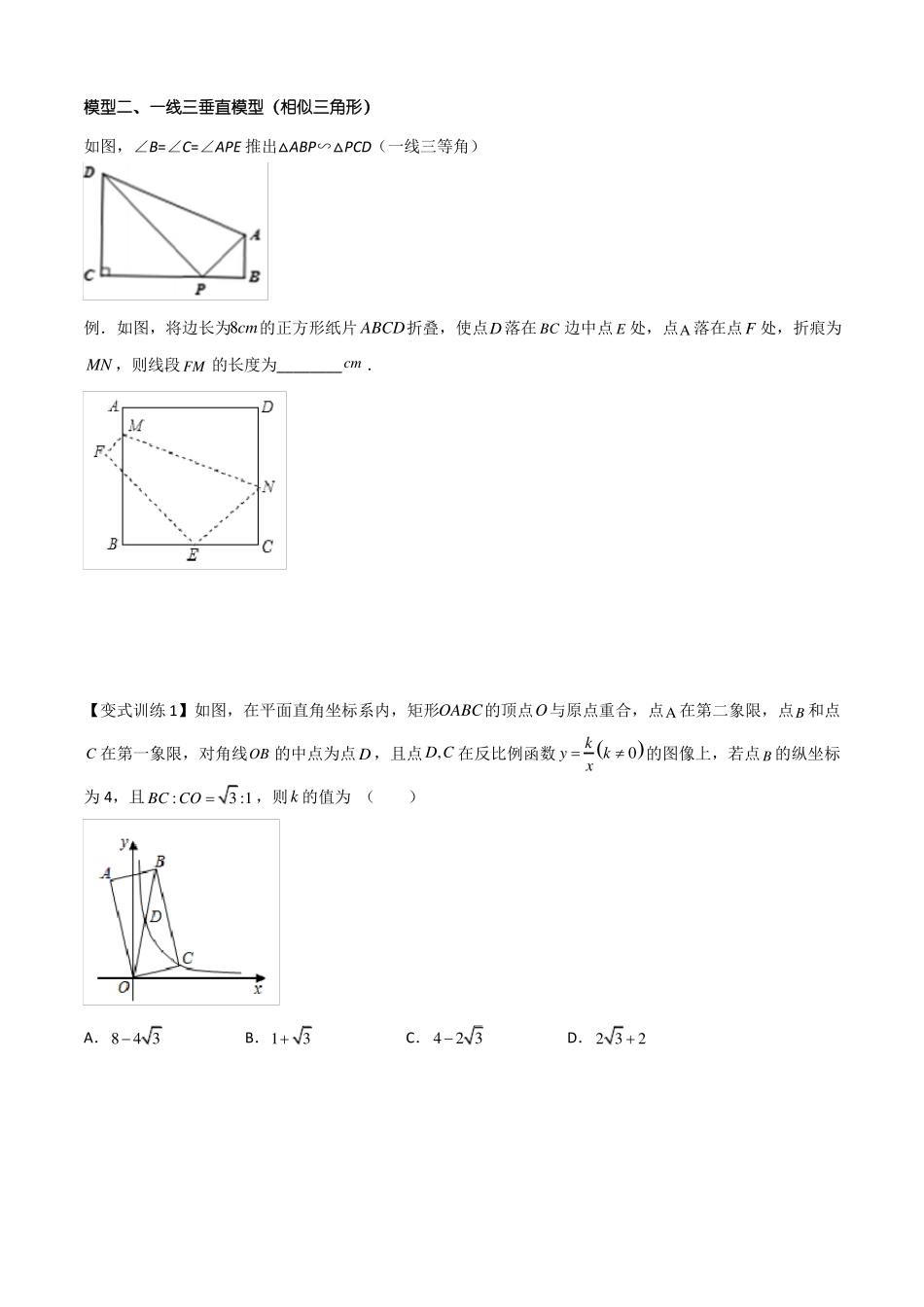
专题05一线三垂直模型模型一、一线三垂直模型（全等三角形）如图所示，∠D=∠BCA=∠E=90°，BC=AC。结论：Rt∠BDC∠Rt∠CEABADEC例.如图，将边长为5正方形OACD放在平面直角坐标系中，О是坐标原点，点D的坐标为横坐标为3，求A的坐标．【变式训练1】如图，ACB90，ACBC，ADCE，BECE，垂足分别为D，E，若AD9，DE6，求BE的长．【变式训练2】如图，A4,0,B0,6，以B点为直角顶点在第一象限作等腰直角ABC，则C点的坐标为_________【变式训练3】在平面直角坐标系中，A0,5,B1,0，点C在第一象限，BAC90，ABAC（1）如图1，求点C的坐标．（2）如图2，作ABC的角平分线BD，交AC于点D，过C点作CEBD于点E，求证：BD2CE（3）若点P在第二象限，且PAB为等腰直角三角形，请直接写出所有满足条件的点P的坐标．模型二、一线三垂直模型（相似三角形）如图，∠B=∠C=∠APE推出△ABP∽△PCD（一线三等角）例．如图，将边长为8cm的正方形纸片ABCD折叠，使点D落在BC边中点E处，点A落在点F处，折痕为MN，则线段FM的长度为________cm．【变式训练1】如图，在平面直角坐标系内，矩形OABC的顶点O与原点重合，点A在第二象限，点B和点C在第一象限，对角线OB的中点为点D，且点D,C在反比例函数y为4，且BC:CO3:1，则k的值为（）kk0的图像上，若点B的纵坐标xA．843B．13C．423D．232【变式训练2】如图，在正方形ABCD中，点E在AD上，EF交CD于点F．（1）求证：ABE（2）连结BF，若ABEDEF；EBF，试确定点E的位置并说明理由．【变式训练3】如图，点B1在直线l:y1x上，点B1的横坐标为2，过点B1作B1l，交x轴于点A1，以A1B12为边，向右作正方形A1B1B2C1，延长B2C1交x轴于点A2；以A2B2为边，向右作正方形A2B2B3C2，延长B3C2交x轴于点A3；以A3B3为边，向右作正方形A3B3B4C3，延长的B4C3交x轴于点A4；…；按照这个规律进行下去，则第n个正方形AnBnBn1Cn的边长为________（结果用含正整数n的代数式表示）．课后训练1.如图，在△ABC中，AB＝AC＝6，D是AC中点，E是BC上一点，BE=2，∠AED＝∠B，则CE的长为（）5A．152B．223C．365D．6492.如图，CDDB，ABDB，且AB6，CD4，DB14，点P是线段DB上一动点，当DP______时，以C、D、P为顶点的三角形与以P、A、B三点为顶点的三角形相似．3.如图，点A为反比例函数y(x0)图象上的一点，以A为直角顶点作等腰直角三角形AOB，点B落在第一象限的反比例函数y18上，已知点B的横坐标是纵坐标的两倍，则k________．xkx4.如图，AB//CD，CDBD且AB6，CD4，BD14，在BD上是否存在一点P，使得以P、B、A为顶点的三角形与以P、D、C为顶点的三角形相似，若存在，求BP的长，若不存在，请说明理由．5.在Rt△ABC中，C90，AC8cm，BC6cm，点D在AC上，且AD6cm，过点A作射线，若点P从点A出发，沿射线AE匀速运动，运动速度为1cm/s，设AEAC（AE与BC在AC同侧）点P运动时间为t秒．连结PD、BD．（1）如图①，当PDBD时，求证：△PDA≌△DBC；（2）如图②，当PDAB于点F时，求此时t的值．6.如图，在矩形ABCD中，E为AD中点，EFEC交AB于F，连结FCABAE．∠△AEF与△ECF是否相似？若相似，证明你的结论；若不相似，请说明理由．∠设AB是否存在这样的k值，使得△AEF与△BFC相似，若存在，证明你的结论，并求出k的值；k，BC若不存在，说明理由．AFEDBC7.如图，已知矩形ABCD中，AB＝4，动点P从点A出发，沿AD方向以每秒1个单位的速度运动，连接BP，作点A关于直线BP的对称点E，设点P的运动时间为t（s）．（1）若AD＝6，P仅在边AD运动，求当P，E，C三点在同一直线上时对应的t的值．（2）在动点P在射线AD上运动的过程中，求使点E到直线BC的距离等于3时对应的t的值．