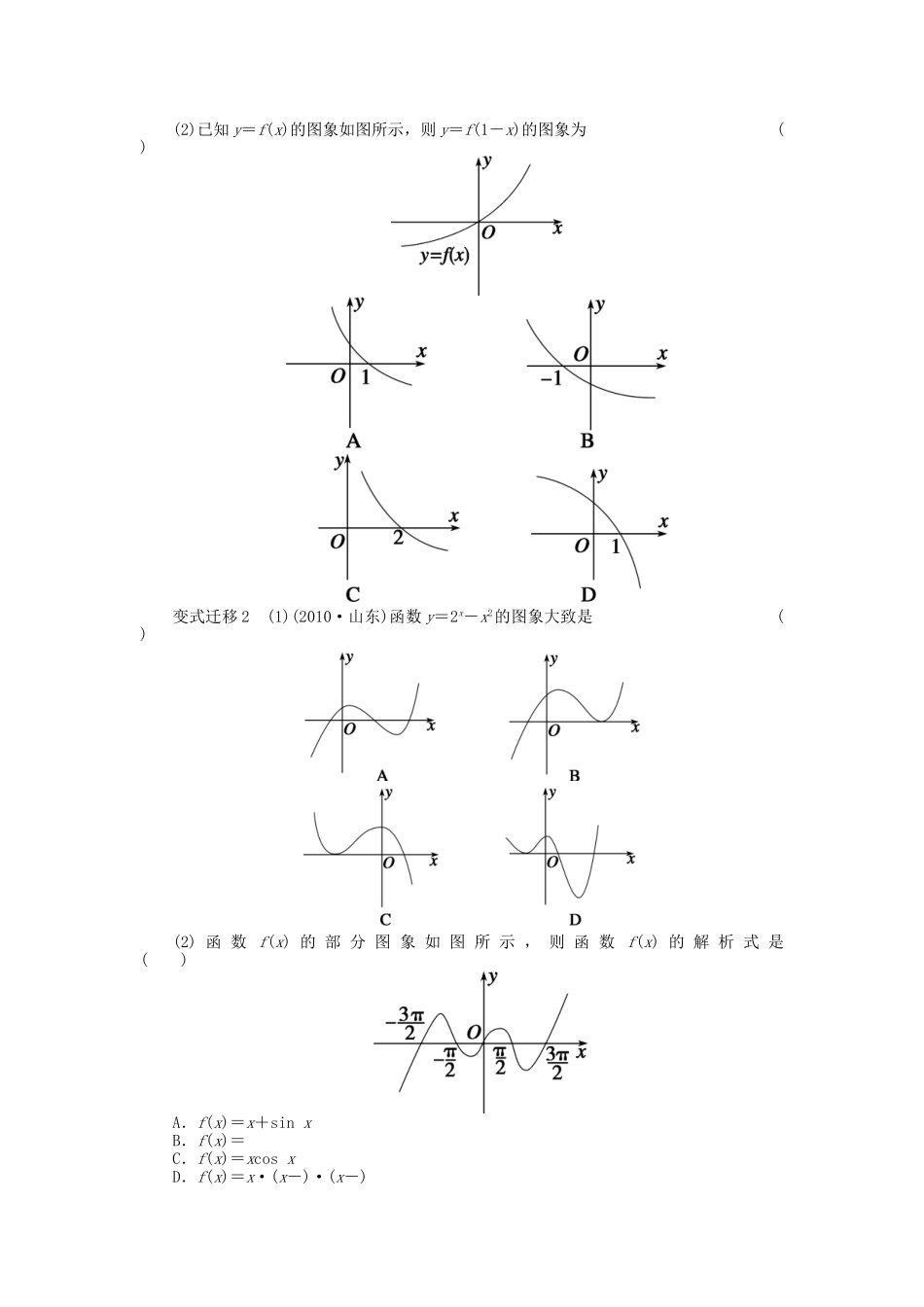
10函数的图象导学目标:1.掌握作函数图象的两种基本方法:描点法,图象变换法.2.掌握图象变换的规律,能利用图象研究函数的性质.自主梳理1.应掌握的基本函数的图象有:一次函数、二次函数、幂函数、指数函数、对数函数等.2.利用描点法作图:①确定函数的定义域;②化简函数的解析式;③讨论函数的性质(__________、__________、__________);④画出函数的图象.3.利用基本函数图象的变换作图:(1)平移变换:函数y=f(x+a)的图象可由y=f(x)的图象向____(a>0)或向____(a<0)平移____个单位得到;函数y=f(x)+a的图象可由函数y=f(x)的图象向____(a>0)或向____(a<0)平移____个单位得到.(2)伸缩变换:函数y=f(ax)(a>0)的图象可由y=f(x)的图象沿x轴伸长(0
0)的图象可由函数y=f(x)的图象沿y轴伸长(____)或缩短(________)为原来的____倍得到.(可以结合三角函数中的图象变换加以理解)(3)对称变换:①奇函数的图象关于________对称;偶函数的图象关于____轴对称;②f(x)与f(-x)的图象关于____轴对称;③f(x)与-f(x)的图象关于____轴对称;④f(x)与-f(-x)的图象关于________对称;⑤f(x)与f(2a-x)的图象关于直线________对称;⑥曲线f(x,y)=0与曲线f(2a-x,2b-y)=0关于点________对称;⑦|f(x)|的图象先保留f(x)原来在x轴________的图象,作出x轴下方的图象关于x轴的对称图形,然后擦去x轴下方的图象得到;⑧f(|x|)的图象先保留f(x)在y轴________的图象,擦去y轴左方的图象,然后作出y轴右方的图象关于y轴的对称图形得到.自我检测1.(2009·北京)为了得到函数y=lg的图象,只需把函数y=lgx的图象上所有的点()A.向左平移3个单位长度,再向上平移1个单位长度B.向右平移3个单位长度,再向上平移1个单位长度C.向左平移3个单位长度,再向下平移1个单位长度D.向右平移3个单位长度,再向下平移1个单位长度2.(2011·烟台模拟)已知图1是函数y=f(x)的图象,则图2中的图象对应的函数可能是()A.y=f(|x|)B.y=|f(x)|C.y=f(-|x|)D.y=-f(-|x|)3.函数f(x)=-x的图象关于()A.y轴对称B.直线y=-x对称C.坐标原点对称D.直线y=x对称4.使log2(-x)0且a≠1),若f(4)·g(-4)<0,则y=f(x),y=g(x)在同一坐标系内的大致图象是()探究点一作图例1(1)作函数y=|x-x2|的图象;(2)作函数y=x2-|x|的图象;(3)作函数的图象.变式迁移1作函数y=的图象.探究点二识图例2(1)函数y=f(x)与函数y=g(x)的图象如图,则函数y=f(x)·g(x)的图象可能是()(2)已知y=f(x)的图象如图所示,则y=f(1-x)的图象为()变式迁移2(1)(2010·山东)函数y=2x-x2的图象大致是()(2)函数f(x)的部分图象如图所示,则函数f(x)的解析式是()A.f(x)=x+sinxB.f(x)=C.f(x)=xcosxD.f(x)=x·(x-)·(x-)探究点三图象的应用例3若关于x的方程|x2-4x+3|-a=x至少有三个不相等的实数根,试求实数a的取值范围.变式迁移3(2010·全国Ⅰ)直线y=1与曲线y=x2-|x|+a有四个交点,则a的取值范围是________.数形结合思想的应用例(5分)(2010·北京东城区一模)定义在R上的函数y=f(x)是减函数,且函数y=f(x-1)的图象关于(1,0)成中心对称,若s,t满足不等式f(s2-2s)≤-f(2t-t2).则当1≤s≤4时,的取值范围是()A.B.C.D.【答题模板】答案D解析因函数y=f(x-1)的图象关于(1,0)成中心对称,所以该函数的图象向左平移一个单位后的解析式为y=f(x),即y=f(x)的图象关于(0,0)对称,所以y=f(x)是奇函数.又y=f(x)是R上的减函数,所以s2-2s≥t2-2t,令y=x2-2x=(x-1)2-1,图象的对称轴为x=1,当1≤s≤4时,要使s2-2s≥t2-2t,即s-1≥|t-1|,当t≥1时,有s≥t≥1≤≤,所以1;当t<1时,即s-1≥1-t,即s+t≥2,问题转化成了线性规划问题,画出由1≤s≤4,t<1,s+t≥2组成的不等式组的可行域.≤为可行域内的点到原点连线的斜率,易知-<1.综上可知选D.【突破思维障碍】当s,t位于对称轴x=1的两边时,如何由s...