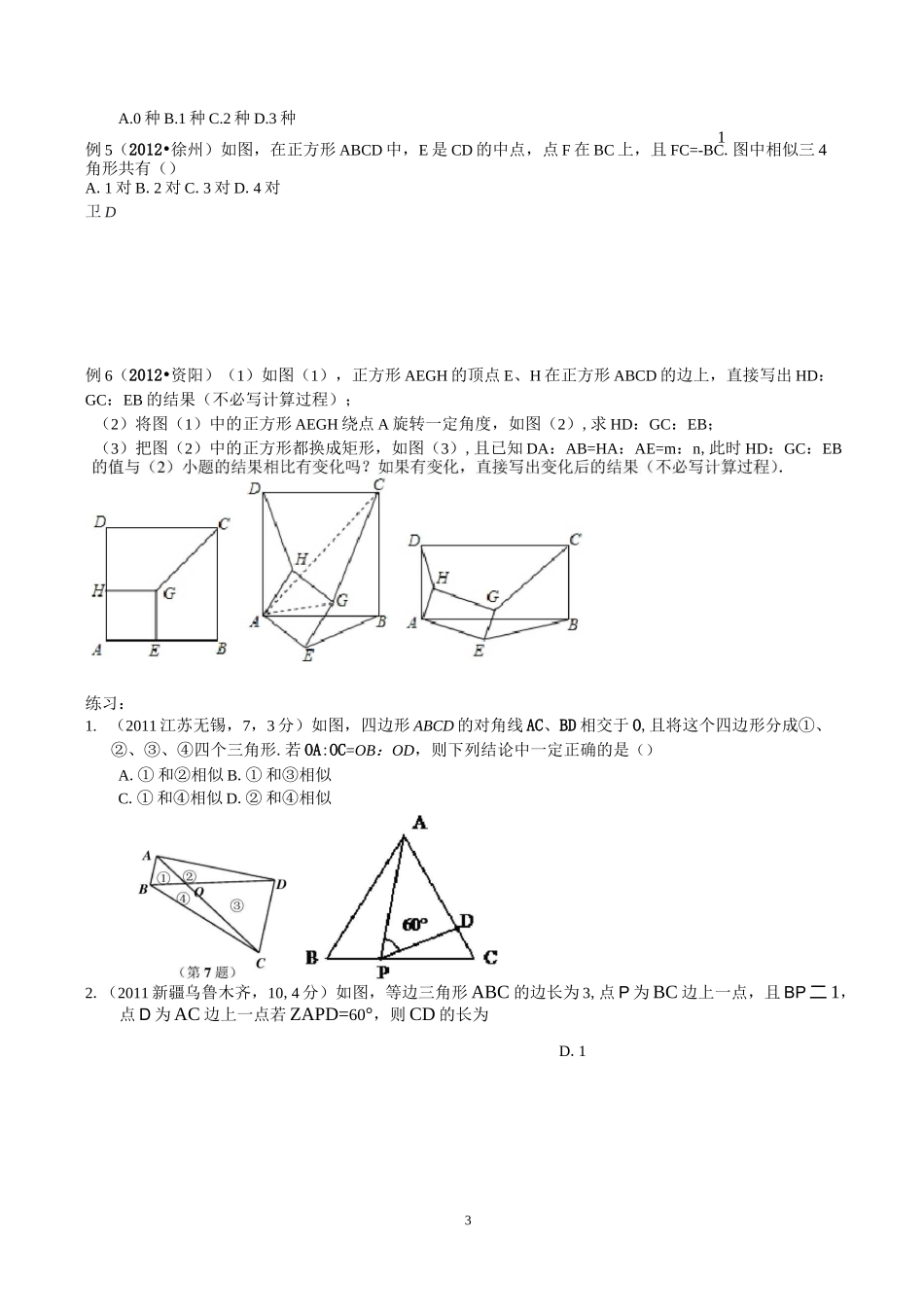
1A.7B.7.5C.8D.8.5老师:学生:年级:日期:时间:()课题目标重难点教学内容1.相似三角形的定义:对应角相等,对应边的比相等的两个三角形。对应边的比叫做相似比。三条平行线截两条直线所得的对应线段的比相等。2.相似三角形的判定:①平行法②三组对应边的比相等(类似于三角形全等判定“SSS”)③两组对应边的比相等,且夹角相等(类似于三角形全等判定“SAS”[④两角对应相等(AA)直角三角形中斜边、直角边对应比相等(类似于直角三角形全等判定“HL”)。相似三角形的基本图形:判断三角形相似,若已知一角对应相等,可先考虑另一角对应相等,注意公共角或对顶角或同角(等角)的余角(或补角)相等,若找不到第二对角相等,就考虑夹这个角的两对应边的比相等;若无法得到角相等,就考虑三组对应边的比相等。3•相似三角形的性质:①对应角相等②对应边的比相等③对应的高、中线、角平分线、周长之比等于相似比④对应的面积之比等于相似比的平方。4•相似三角形的应用:求物体的长或宽或高;求有关面积等。(三)考点精讲考点一:平行线分线段成比例例1、(2011广东肇庆)如图,已知直线a〃b〃c,直线m、n与a、b、交于点A、C、E、B、D、F,AC=4,CE=6,BD=3,则BF=abc2D.42.(2011山东泰安,15,3分)如图,点F是□ABCD的边CD上一点,直线BF交AD的延长线于点E,则F列结论错误的是()ED_DFDE_EF~B^~~FBBCBFBFBCCD.~BE~~AE考点二:相似三角形的判A.1对B.2对C.3对D.4对例2(2012•福州)如图,已知△ABC,AB=AC=1,ZA=36°,ZABC的平分线BD交AC于点D,则AD的长是,cosA的值是.(结果保留根号)练习:1.(2011湖南怀化,6,3)如图所示:A4BC中,DEHBC,AD=5,BD=10,AE=3,则CE的值为()3.(2012•孝感)如图,在△ABC中,AB=AC,ZA=36°,BD平分ZABC交AC于点D,若AC=2,则AD的长是()例3、(2011湖北荆州)如图,P为线段AB上一点,AD与BC交于E,ZCPD=ZA=ZB,BC交PD于F,AD交PC于G,则图中相似三角形有()例4、(2010江苏泰州)一个铝质三角形框架三条边长分别为24cm、30cm、36cm,要做一个与它相似的铝质三角形框架,现有长为27cm、45cm的两根铝材,要求以其中的一根为一边,从另一根上截下两段(允许有余料)作为另外两边•截法有()B3A.0种B.1种C.2种D.3种1例5(2012•徐州)如图,在正方形ABCD中,E是CD的中点,点F在BC上,且FC=-BC.图中相似三4角形共有()A.1对B.2对C.3对D.4对卫D例6(2012•资阳)(1)如图(1),正方形AEGH的顶点E、H在正方形ABCD的边上,直接写出HD:GC:EB的结果(不必写计算过程);(2)将图(1)中的正方形AEGH绕点A旋转一定角度,如图(2),求HD:GC:EB;(3)把图(2)中的正方形都换成矩形,如图(3),且已知DA:AB=HA:AE=m:n,此时HD:GC:EB练习:1.(2011江苏无锡,7,3分)如图,四边形ABCD的对角线AC、BD相交于O,且将这个四边形分成①、②、③、④四个三角形.若OA:OC=OB:OD,则下列结论中一定正确的是()A.①和②相似B.①和③相似C.①和④相似D.②和④相似2.(2011新疆乌鲁木齐,10,4分)如图,等边三角形ABC的边长为3,点P为BC边上一点,且BP二1,点D为AC边上一点若ZAPD=60°,则CD的长为D.1(例5)43.(2012•攀枝花)如图,△ABC9AADE且ZABC=ZADE,ZACB=ZAED,BC、DE交于点O.则下列四个结论中,①Z1=Z2;②BC=DE;③、ABDs^ACE;④A、O、C、E四点在同一个圆上,一定成立的有()A.1个B.2个C.3个D.4个4.(2012•义乌市)在锐角△ABC中,AB=4,BC=5,ZACB=45°,将AABC绕点B按逆时针方向旋转,得到△A1BC1.(1)如图1,当点C1在线段CA的延长线上时,求ZCC1A1的度数;(2)如图2,连接AA1,CC1.若厶ABA]的面积为4,求ACBC]的面积;(3)如图3,点E为线段AB中点,点P是线段AC上的动点,在厶ABC绕点B按逆时针方向旋转过程中,点P的对应点是点P],求线段EP1长度的最大值与最小值.考点二:相似二角形的性质例7、(2010山东烟台)如图,△ABC中,点D在线段BC上,且△ABC^ADBA,则下列结论一定正确的是()A.AB2=BC・BDB.AB2=ACBDC.AB・AD=BD・BCD.AB・AD=AD・CD例8、(2011浙江嘉兴)如图,边长为4的等边AABC中,DE为中位线,贝四边形BCED的面积为()(A)2込(B)3•打5(C)4、;3(D)6\;3...