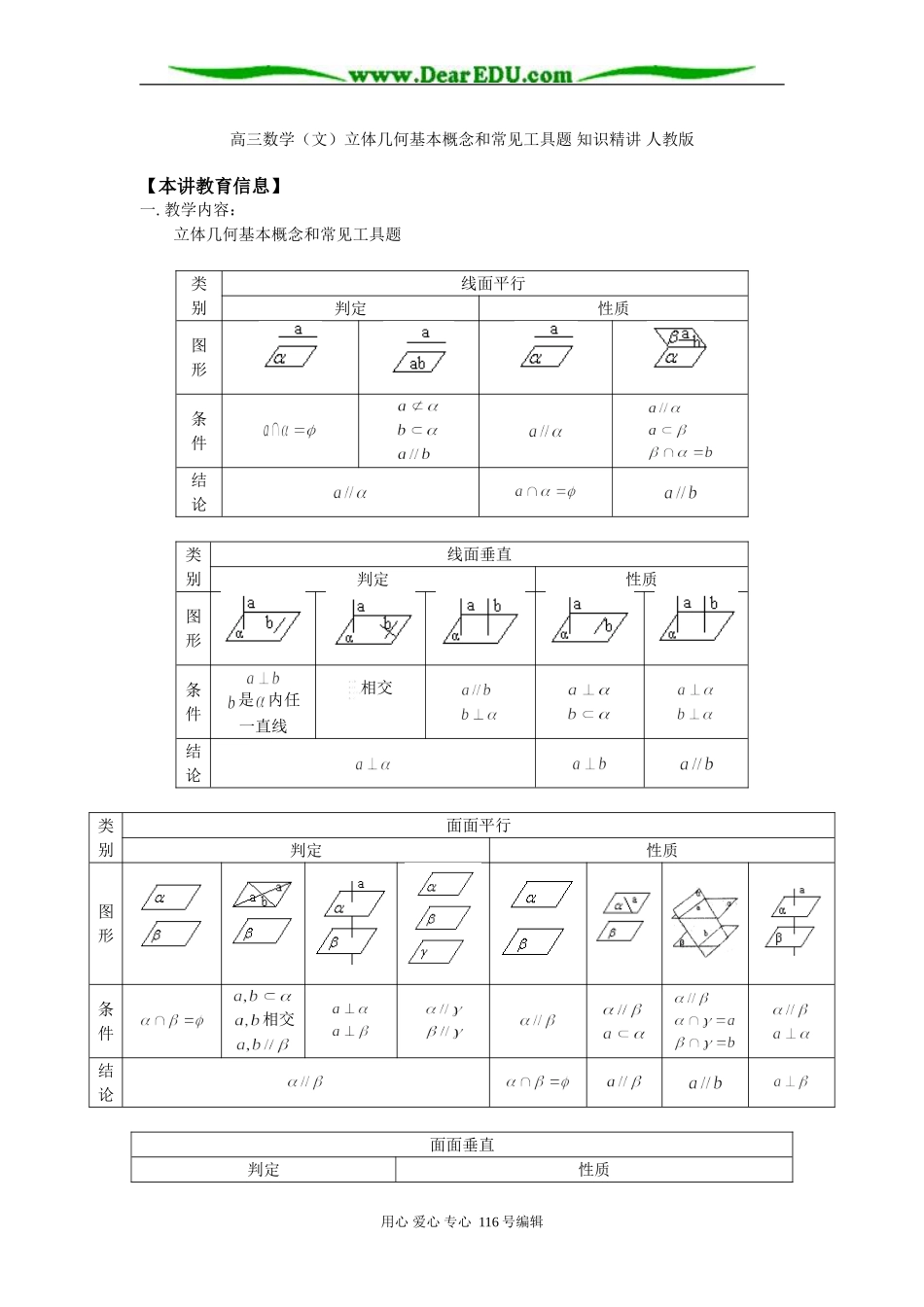
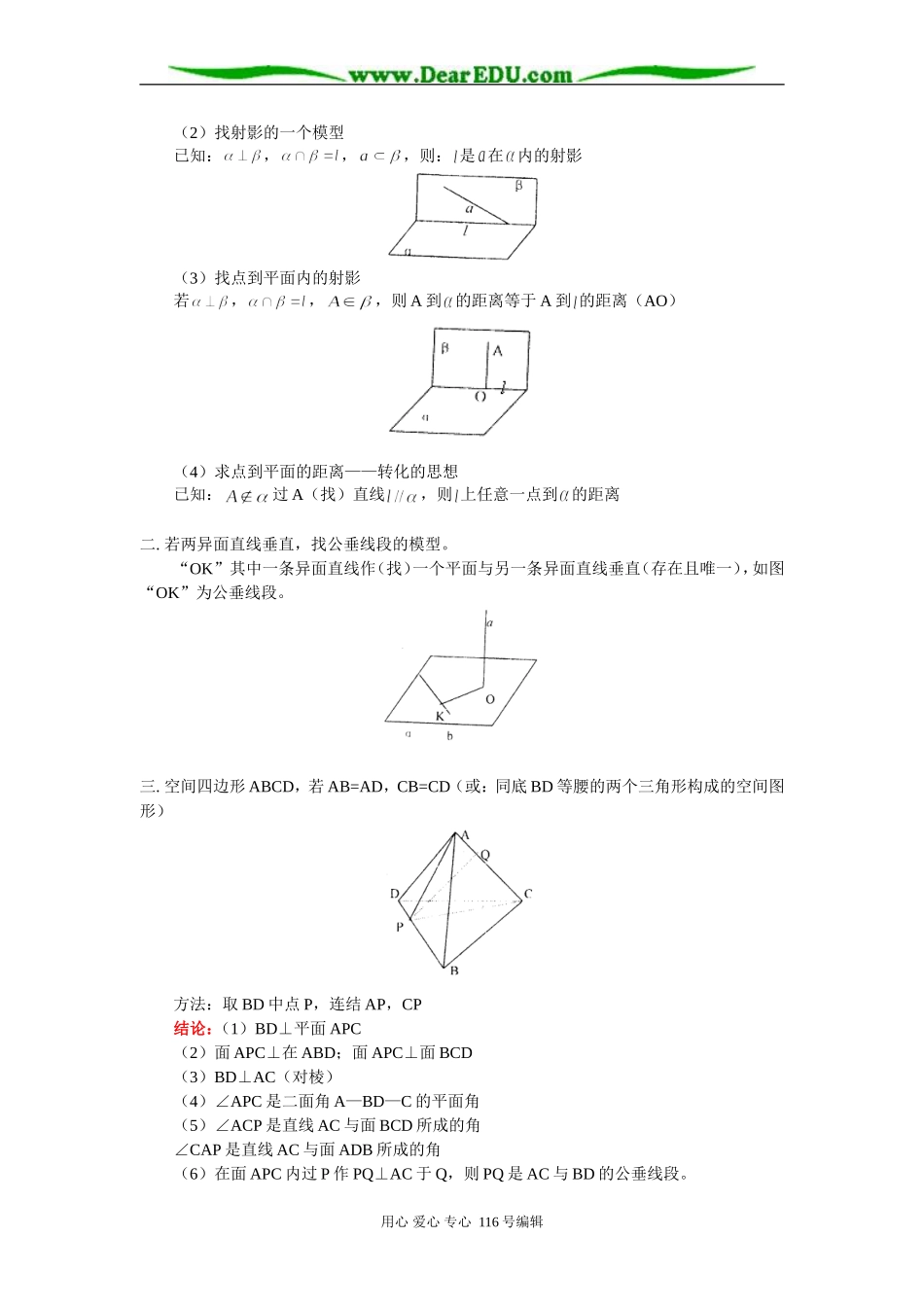
高三数学(文)立体几何基本概念和常见工具题知识精讲人教版【本讲教育信息】一.教学内容:立体几何基本概念和常见工具题类别线面平行判定性质图形条件结论类别线面垂直判定性质图形条件是内任一直线相交结论类别面面平行判定性质图形条件相交结论面面垂直判定性质用心爱心专心116号编辑是二面角的平面角,是二面角的平面角,平行的判定方法直线与直线直线与平面平面与平面1定义:定义:2345垂直的判定方法直线与直线直线与平面平面与平面1定义:定义:定义:与成的二面角234三垂线定理:56注:注重三种语言的学习:文字语言、图形语言、符号语言——三者是一个统一的整体。几个实用的工具题一.(1)证明几点共线的模型用心爱心专心116号编辑(2)找射影的一个模型已知:,,,则:是在内的射影(3)找点到平面内的射影若,,,则A到的距离等于A到的距离(AO)(4)求点到平面的距离——转化的思想已知:过A(找)直线,则上任意一点到的距离二.若两异面直线垂直,找公垂线段的模型。“OK”其中一条异面直线作(找)一个平面与另一条异面直线垂直(存在且唯一),如图“OK”为公垂线段。三.空间四边形ABCD,若AB=AD,CB=CD(或:同底BD等腰的两个三角形构成的空间图形)方法:取BD中点P,连结AP,CP结论:(1)BD⊥平面APC(2)面APC⊥在ABD;面APC⊥面BCD(3)BD⊥AC(对棱)(4)∠APC是二面角A—BD—C的平面角(5)∠ACP是直线AC与面BCD所成的角∠CAP是直线AC与面ADB所成的角(6)在面APC内过P作PQ⊥AC于Q,则PQ是AC与BD的公垂线段。用心爱心专心116号编辑(7)由(2)知:过A作面BCD,垂足为,则一定在PC或PC延长线上。同理,过C作面ADB的垂线,垂足在哪儿?四.P为△ABC所在平面外一点,点P在平面ABC的射影为O。(1)若PA=PB=PC,则O为△ABC的外心(2)若P到三边AB、BC、CA的距离相等,则O是△ABC的内心或旁心。(3)若PA、PB、PC两两垂直,则O是△ABC的垂心。(4)若△ABC为正三角形,具备(1)、(2)、(3)条件之一时,则O是△ABC的中心。(5)若△ABC是Rt△,且PA=PB=PC,则O是△ABC斜边中点。五.如图在平面内,AP是平面的一条斜线。(1)若∠APC=∠APB(2)若A到PB,PC边距离相等。(3)AP在的射影是∠BPC的平分线以上三条有一个成立,便可推出另两个结论。即三组Rt△:,,若有一组全等,则另两组必全等。【典型例题】[例1]在空间四边形ABCD中,E、F分别为AB、CD的中点,若AD=BC,且AD与BC成60°用心爱心专心116号编辑角,则异面直线EF和BC所成角的大小为()A.30°B.60°C.30°或60°D.90°答案:C[例2]在正三棱柱ABC—A1B1C1中,若,则异面直线A1B与CC1所成角的大小为。解:由A1A//C1C,则∠BA1A为A1B与C1C所成的角由答案:[例3]如图所示,正三棱锥A—BCD中,E、F分别为棱AB、CD的中点,设为EF与AC所成的角,为EF与BD所成的角,则+等于()A.B.C.D.解:如图,取BC中点G,连FG,EG,则FG//BD,EG//AC,则∠GEF=,∠GFE=,又∠EGF为AC与BD所成的角容易证明,AC⊥BD,则∠EGF=90°,故+=90°答案:D[例4]把正方形ABCD沿对角线AC折起,当以A、B、C、D四点为顶点的三棱锥体积最大时,异面直线AD与BC的夹角为()A.30°B.45°C.60°D.90°解:当且仅当△ADC与△ABC垂直时四面体ABCD体积最大,取AC中点O,则DO⊥面ABC,且AO=BO=取BD,AB中点E,F,连EF,FO,EO,则,又BD=,则EF=FO=EO=用心爱心专心116号编辑又∠EFO为AD与BC所成的角,则AD与BC所成角为60°(利用异面直线上两点间距离公式)[例5]如图在棱长为的正方体ABCD—A1B1C1D1中,分别由A1,D1向B1D作垂线A1E,D1F,E,F为垂足,求异面直线D1F和A1E所成的角。解:连D1B1和A1D,则在Rt△DD1B1中,由同理,在Rt△DA1B1中,在Rt△DD1F中,,在中,∴设所求异面直线D1F和A1E所成的角为,则∴60°[例6]正四面体ABCD的棱长为,E为棱CD上一点,,求异面直线AE与BC间的距离。用心爱心专心116号编辑解:在△ACE中,AC=,CE=,∠ACE=60°过E作EF//BC交BD于F,则∠AEF是异面直线AE与BC所成的角又由△AEF为等腰三角形,故又于是[例7]在四面体ABCD中,设AB=1,,直线AB与CD的距离为2,夹角为,求四面体ABCD的体积。解:如图,过C作...