高三数学（文科）主干知识三 立体几何 新人教A版VIP免费

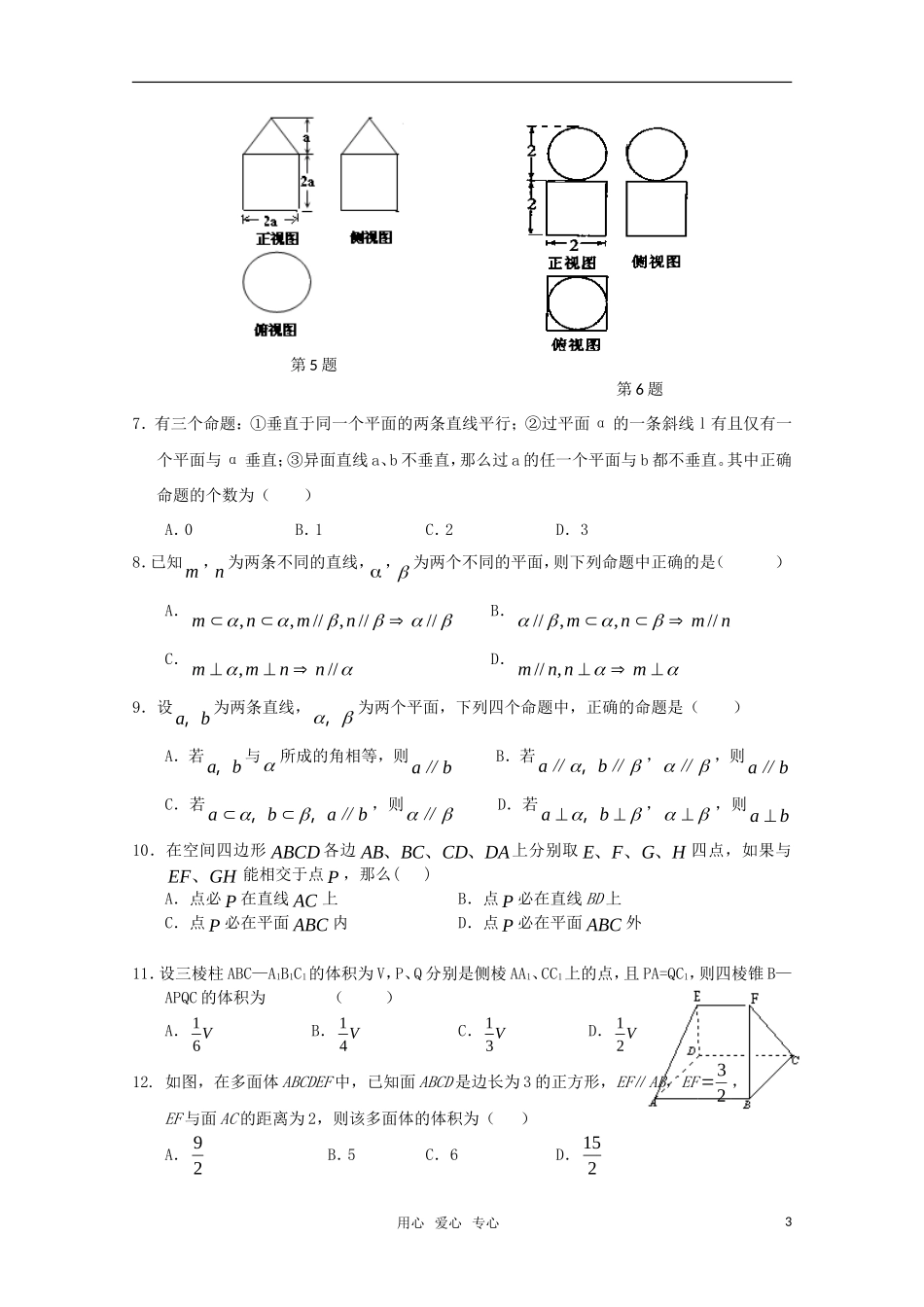
高三数学（文科）主干知识三：立体几何考试要求（1）空间几何体①认识柱、锥、台、球及其简单组合体的结构特征．②能画出简单空间图形（长方体、球、圆柱、圆锥、棱柱等的简易组合）的三视图，能识别上述的三视图所表示的立体模型，会用斜二侧法画出它们的直观图．③了解球、棱柱、棱锥、台的表面积和体积的计算公式（不要求记忆公式）．（2）点、直线、平面之间的位置关系①理解空间直线、平面位置关系的定义，并了解如下可以作为推理依据的公理和定理．◆公理1：如果一条直线上的两点在一个平面内，那么这条直线上所有的点在此平面内．◆公理2：过不在同一条直线上的三点，有且只有一个平面．◆公理3：如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线．◆公理4：平行于同一条直线的两条直线互相平行◆定理：空间中如果一个角的两边与另一个角的两边分别平行，那么这两个角相等或互补．②以立体几何的上述定义、公理和定理为出发点，认识和理解空间中线面平行、垂直的有关性质与判定．理解以下判定定理：◆如果平面外一条直线与此平面内的一条直线平行，那么该直线与此平面平行．◆如果一个平面内的两条相交直线与另一个平面都平行，那么这两个平面平行．◆如果一条直线与一个平面内的两条相交直线都垂直，那么该直线与此平面垂直．◆如果一个平面经过另一个平面的垂线，那么这两个平面互相垂直．理解以下性质定理，并能够证明：◆如果一条直线与一个平面平行，经过该直线的任一个平面与此平面相交，那么这条直线就和交线平行．◆如果两个平行平面同时和第三个平面相交，那么它们的交线相互平行◆垂直于同一个平面的两条直线平行◆如果两个平面垂直，那么一个平面内垂直于它们交线的直线与另一个平面垂直．③能运用公理、定理和已获得的结论证明一些空间位置关系的简单命题．复习关注：立体几何试题着重考查空间点、线、面的位置关系的判断及几何体的表面积与体积的计算，关注画图、识图、用图的能力，关注对平行、垂直的探究，关注对条件或结论不完备情景下的开放性问题的探究．强化训练一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题意要求的.1．如图，一个空间几何体的主视图、左视图、俯视图为全等的等腰直角三角形，如果直角三角形的直角边长为1，那么这个几何体的体积为（）.A.1B.12C.13D.162．如果一个几何体的三视图如图所示(单位长度:cm),则此几何体的表面积是()用心爱心专心1A.2(2042)cmB.221cmC.2(2442)cmD.224cm3．如图,水平放置的三棱柱的侧棱长和底边长均为2，且侧棱1111AAABC面,正视图是边长为2的正方形，该三棱柱的左视图面积为（）A.4B.32C.22D.34．如图所示，一个空间几何体的主视图和左视图都是边长为1的正方形，俯视图是一个直径为1的圆，那么这个几何体的全面积为（）A．3π2B．2πC．3πD．4π5．已知一个几何体的三视图如图所示，则此几何体的表面积是（）A．4πa2B．3πa2C．(5+)πa2D．(3+)πa26．下图表示一个几何体的三视图及相应数据，则该几何体的体积（）A．348B．344C．48D．310用心爱心专心2左视图主视图俯视图2俯视图主视图左视图212_B_1_A_1_B_A_B_1_A_1_B_A正视图俯视图第3题第2题主视图左视图俯视图第1题第4题7．有三个命题：①垂直于同一个平面的两条直线平行；②过平面α的一条斜线ｌ有且仅有一个平面与α垂直；③异面直线a、b不垂直，那么过a的任一个平面与b都不垂直。其中正确命题的个数为（）A．0B．1C．2D．38．已知m，n为两条不同的直线，，为两个不同的平面，则下列命题中正确的是（）A．,,//,////mnmnB．//,,//mnmnC．,//mmnnD．//,mnnm9．设ab，为两条直线，，为两个平面，下列四个命题中，正确的命题是（）A．若ab，与所成的角相等，则ab∥B．若ab，∥∥，∥，则ab∥C．若abab，，∥，则∥D．若ab，，，则ab10．在空间四边形ABCD各边ABBCCDDA、、、上分别取EFGH、、、四点，如果与EFGH、能相交于点P，那么()A．点必P在直线AC上B...