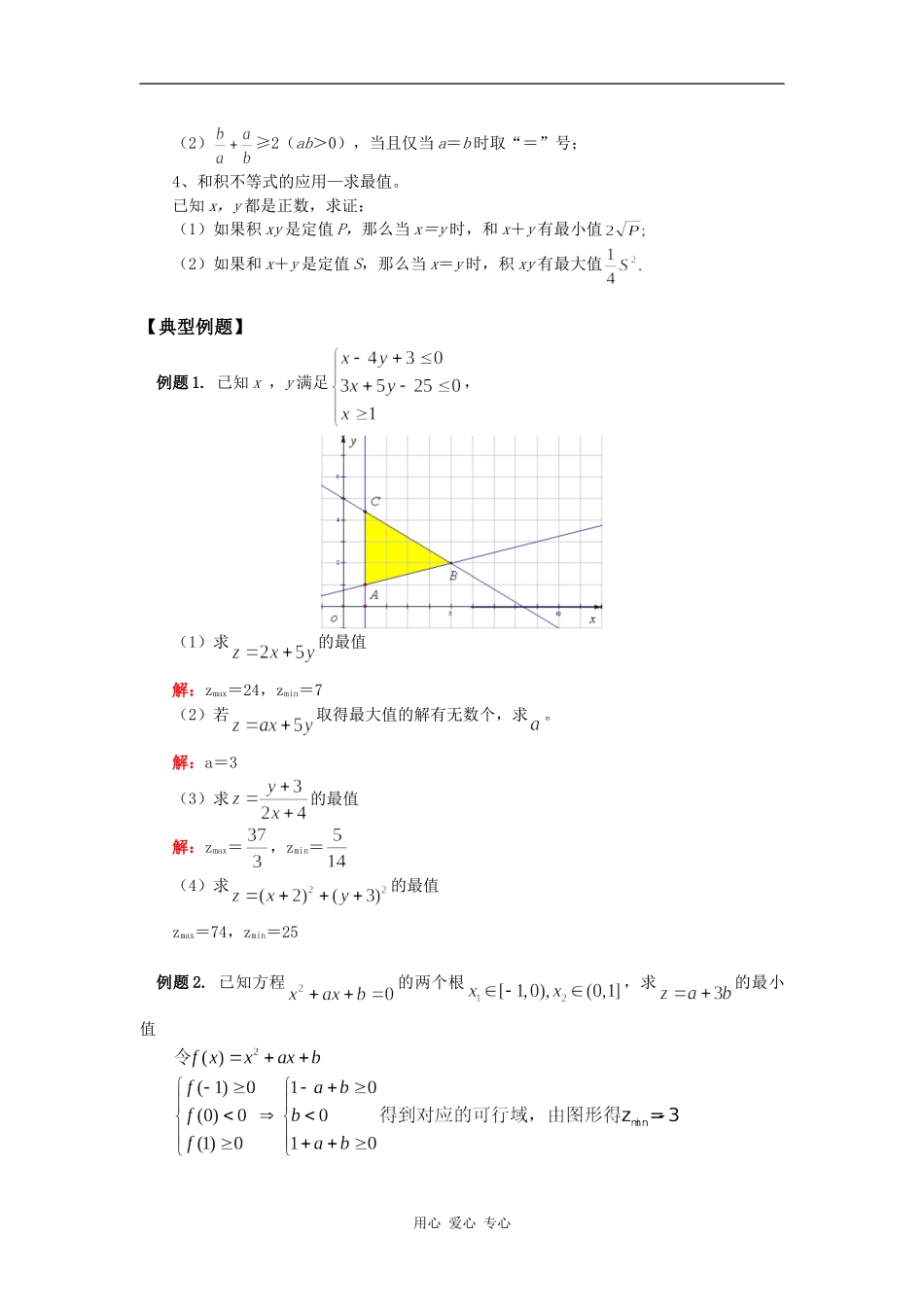
高三数学线性规划与基本不等式苏教版(文)【本讲教育信息】一.教学内容:线性规划与基本不等式二.教学要求:1、能从实际情境中抽象出二元一次不等式组;了解二元一次不等式的几何意义,能用平面区域表示二元一次不等式组。2、能从实际情境中抽象出一些简单的二元线性规划问题,并能加以解决(一般的最优整数解问题不作要求)。3、掌握基本不等式≤(a≥0,b≥0);能用基本不等式证明简单不等式(指只用一次基本不等式即可解决的问题);能用基本不等式求解简单的最大(小)值问题(指只用一次基本不等式即可解决的问题)。三.教学重点、难点:教学重点:基本不等式与线性规划的几何意义教学难点:线性规划的几何意义与基本不等式的使用条件,以及变形使用基本不等式。四.知识归纳:1、线性规划:(1)二元一次不等式Ax+By+C>0在平面直角坐标系中表示直线Ax+By+C=0某一侧所有点组成的平面区域。(虚线表示区域不包括边界直线)。(2)目标函数,线性目标函数线性规划问题,可行解,可行域,最优解。(3)用图解法解决简单的线性规划问题的基本步骤:①根据线性约束条件画出可行域(即不等式组所表示的公共区域);②设t=0,画出直线;③观察、分析,平移直线,从而找到最优解;④最后求得目标函数的最大值及最小值。(4)求线性目标函数在线性约束条件下的最优解的格式与步骤:①寻找线性约束条件,线性目标函数;②由二元一次不等式表示的平面区域做出可行域;③在可行域内求目标函数的最优解。2、重要不等式:(1)如果(2)定理:如果a,b是正数,那么3、公式的等价变形:(1)ab≤,ab≤()2。用心爱心专心(2)≥2(ab>0),当且仅当a=b时取“=”号;4、和积不等式的应用—求最值。已知x,y都是正数,求证:(1)如果积xy是定值P,那么当x=y时,和x+y有最小值(2)如果和x+y是定值S,那么当x=y时,积xy有最大值【典型例题】例题1.已知x,y满足,(1)求的最值解:zmax=24,zmin=7(2)若取得最大值的解有无数个,求。解:a=3(3)求的最值解:zmax=,zmin=(4)求的最值zmax=74,zmin=25例题2.已知方程的两个根,求的最小值用心爱心专心例题3.给出四个命题:(1)的最小值为2;(2)的最大值为(3)的最小值为2;(4)的最小值为4。其中正确命题的个数是(B)A.0B.1C.2D.3例题4.若关于x的方程有实根,求实数a的取值范围。解:令t=2x则原方程可化为t2+at+a+1=0有正数解。法一、变量分离法:。法二、求根公式法:由求根公式得两个根为:则问题等价于大根大于0。所以有法三、分类讨论:即原方程有两个正根;0与一个正根;一个正根与一个负根。例题5.设a、bR,试比较,,,的大小解:应该是:例题6.已知a,b,x,y∈R+(a,b为常数),,求x+y的最小值.当且仅当时,有最小值为用心爱心专心例题7.甲、乙两地相距s(千米),汽车从甲地匀速行驶到乙地,速度最大不得超过c(千米/小时)已知汽车每小时的运输成本(元)由可变部分与固定部分组成.可变部分与速度v(千米/小时)的平方成正比,且比例系数为正常数b;固定部分为a元.(1)试将全程运输成本y(元)表示成速度v(千米/小时)的函数。(2)为使全程运输成本最省,汽车应以多大速度行驶?解:(1)依题意知汽车从甲地匀速行驶到乙地所用时间为,全程运输成本为故所求函数及其定义域为(2)依题意知s,a,b,v都为正数,故有当且仅当即时上式中等号成立若,则当时,全程运输成本y最小,若,则当时,有=因为c-v≥0,且a>bc2,故有a-bcv≥a-bc2>0,所以,且仅当v=c时等号成立,也即当v=c时,全程运输成本y最小.综上知,为使全程运输成本y最小,当时行驶速度应为;当时行驶速度应为v=c.【模拟试题】(答题时间:60分钟)1.不等式组{,表示的平面区域是一个()A.三角形B.梯形C.矩形D.菱形2.设a、b∈R,已知命题p:a=b;命题q:()2≤()A.必要不充分条件B.充分不必要条件用心爱心专心C.充要条件D.既不充分也不必要条件3.设x,y∈R+,且xy-(x+y)=1,则()A.x+y≥2(+1)B.xy≤+1C.x+y≤(+1)2D.xy≥2(+1)4.不等式组的整数解共有_______组.5.某公司一年购买某种货物40...