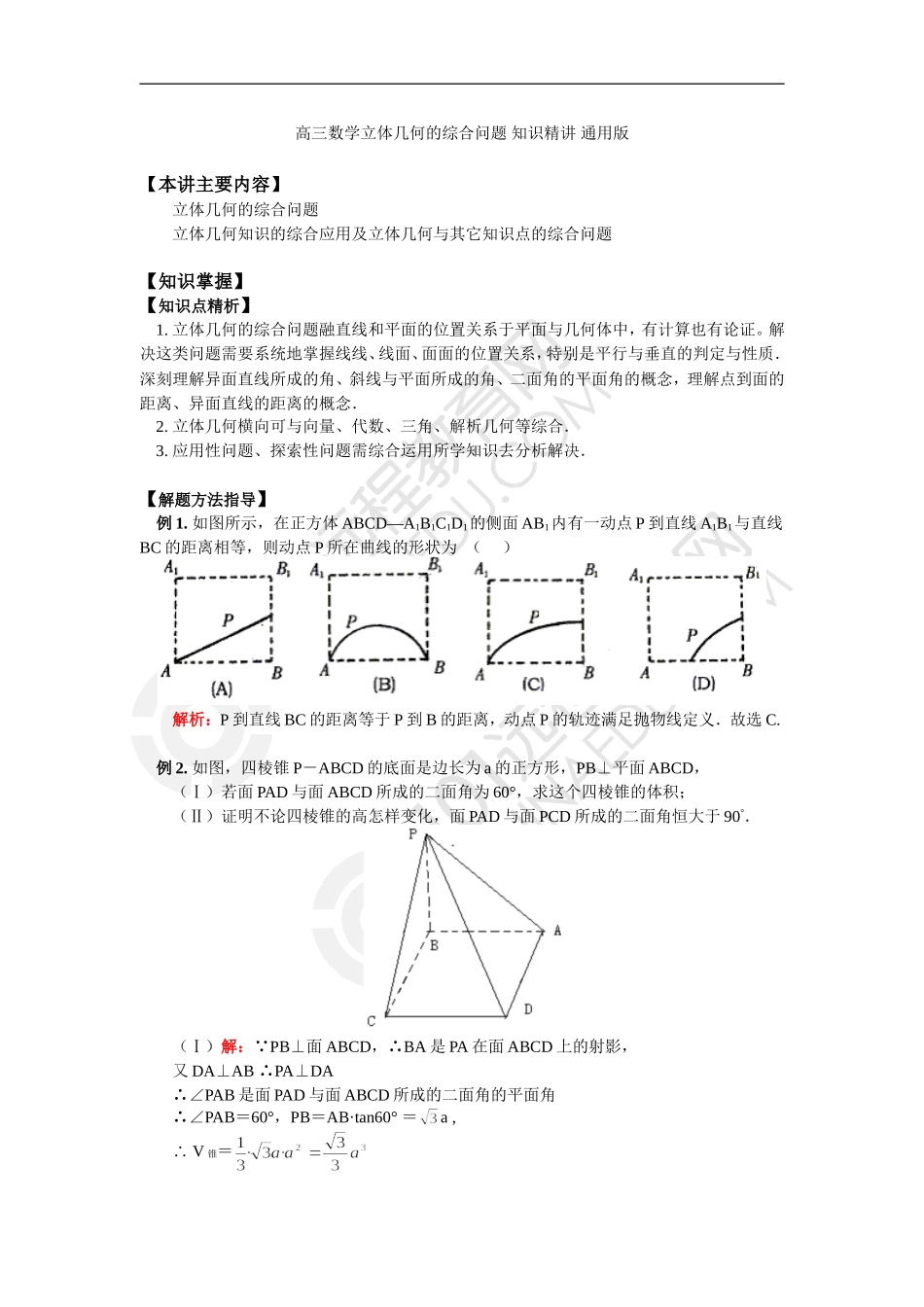
高三数学立体几何的综合问题知识精讲通用版【本讲主要内容】立体几何的综合问题立体几何知识的综合应用及立体几何与其它知识点的综合问题【知识掌握】【知识点精析】1.立体几何的综合问题融直线和平面的位置关系于平面与几何体中,有计算也有论证。解决这类问题需要系统地掌握线线、线面、面面的位置关系,特别是平行与垂直的判定与性质.深刻理解异面直线所成的角、斜线与平面所成的角、二面角的平面角的概念,理解点到面的距离、异面直线的距离的概念.2.立体几何横向可与向量、代数、三角、解析几何等综合.3.应用性问题、探索性问题需综合运用所学知识去分析解决.【解题方法指导】例1.如图所示,在正方体ABCD—A1B1C1D1的侧面AB1内有一动点P到直线A1B1与直线BC的距离相等,则动点P所在曲线的形状为()解析:P到直线BC的距离等于P到B的距离,动点P的轨迹满足抛物线定义.故选C.例2.如图,四棱锥P-ABCD的底面是边长为a的正方形,PB⊥平面ABCD,(Ⅰ)若面PAD与面ABCD所成的二面角为60°,求这个四棱锥的体积;(Ⅱ)证明不论四棱锥的高怎样变化,面PAD与面PCD所成的二面角恒大于90°.(Ⅰ)解: PB⊥面ABCD,∴BA是PA在面ABCD上的射影,又DA⊥AB∴PA⊥DA∴∠PAB是面PAD与面ABCD所成的二面角的平面角∴∠PAB=60°,PB=AB·tan60°=a,∴V锥=(Ⅱ)证明:不论棱锥的高怎样变化,棱锥侧面PAD与PCD恒为等腰三角形,作AE⊥PD,垂足为E,连结CE,则△ADE≌△CDE,因为AE=CE,∠CED=90o,故∠CEA是面PAD与面PCD所成的二面角的平面角.设AC与BD交于点O,连结EO,则EO⊥AC,所以,,在△AEC中,所以面PAD与面PCD所成的二面角恒大于90o。【考点突破】【考点指要】1.高考试卷中,立体几何的考查的立足点放在空间形体和空间图形上,突出对空间概念和空间想象能力的考查.空间图形中的有关计算离不开角与距离、面积与体积等基本量,空间图形中的有关证明离不开平行与垂直这两种基本性质,这些不仅是立体几何的重要内容,也是每年高考的必考内容.另外在高考命题上也常对一些有关概念和常用方法进行迁延性考查,设计出一些颇有新意的考题。对于空间想象能力,高考试题中,侧重于直线与直线、直线与平面、平面与平面的各种位置关系的考查,着重考查图形辨识、几何元素的位置关系和几何量的计算,将逻辑推理及计算能力联系起来,进行综合考查。2.高考立体几何题目设计的立意是:坚持考查逻辑推理能力和空间想象能力。近几年题目的证明强度有所减弱,证明的起点增高,并常常借助多面体或球体作为依托,把论证与计算的几何问题寓于其间,带有一定的综合性。3.在知识的交汇点出命题,是高考命题的趋势,近几年的考试题中,出现了将立体几何与向量、三角、代数、解析几何联系在一起的题目,令人耳目一新,也更突出了对学生综合运用知识的能力及创新能力的考查.分值约占5~10分.【典型例题分析】例1.(2004年高考天津卷理科19)如图,在四棱锥P—ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥PB交PB于点F.(Ⅰ)证明PA//平面EDB;(Ⅱ)证明PB⊥平面EFD;(Ⅲ)求二面角C—PB—D的大小.解法1:(Ⅰ)证明:连结AC,AC交BD于O,连结EO。 底面ABCD是正方形,∴点O是AC的中点在中,EO是中位线,∴PA//EO;而平面EDB且平面EDB,所以,PA//平面EDB(Ⅱ)证明: PD⊥底面ABCD且底面ABCD,∴ PD=DC,可知是等腰直角三角形,而DE是斜边PC的中线,∴.①同样由PD⊥底面ABCD,得PD⊥BC. 底面ABCD是正方形,有DC⊥BC,∴BC⊥平面PDC。而平面PDC,∴.②由①和②推得平面PBC.而平面PBC,∴又且,所以PB⊥平面EFD.(Ⅲ)由(Ⅱ)PB⊥平面EFD,∴,,故是二面角C—PB—D的平面角.由DE⊥平面PBC且EF平面PBC,∴DE⊥EF.又 PD⊥底面ABCD且BD底面ABCD,∴PD⊥DB设正方形ABCD的边长为a,则,,.在中,。在中,,∴.所以,二面角C—PB—D的大小为.解法2:如图所示建立空间直角坐标系,D为坐标原点,设.(Ⅰ)证明:连结AC,AC交BD于G,连结EG.依题意得. 底面ABCD是正方形,∴G是此正方形的中心,故点G的坐标为且.∴,这表明PA//EG.而平面EDB且平面EDB,∴PA//平...