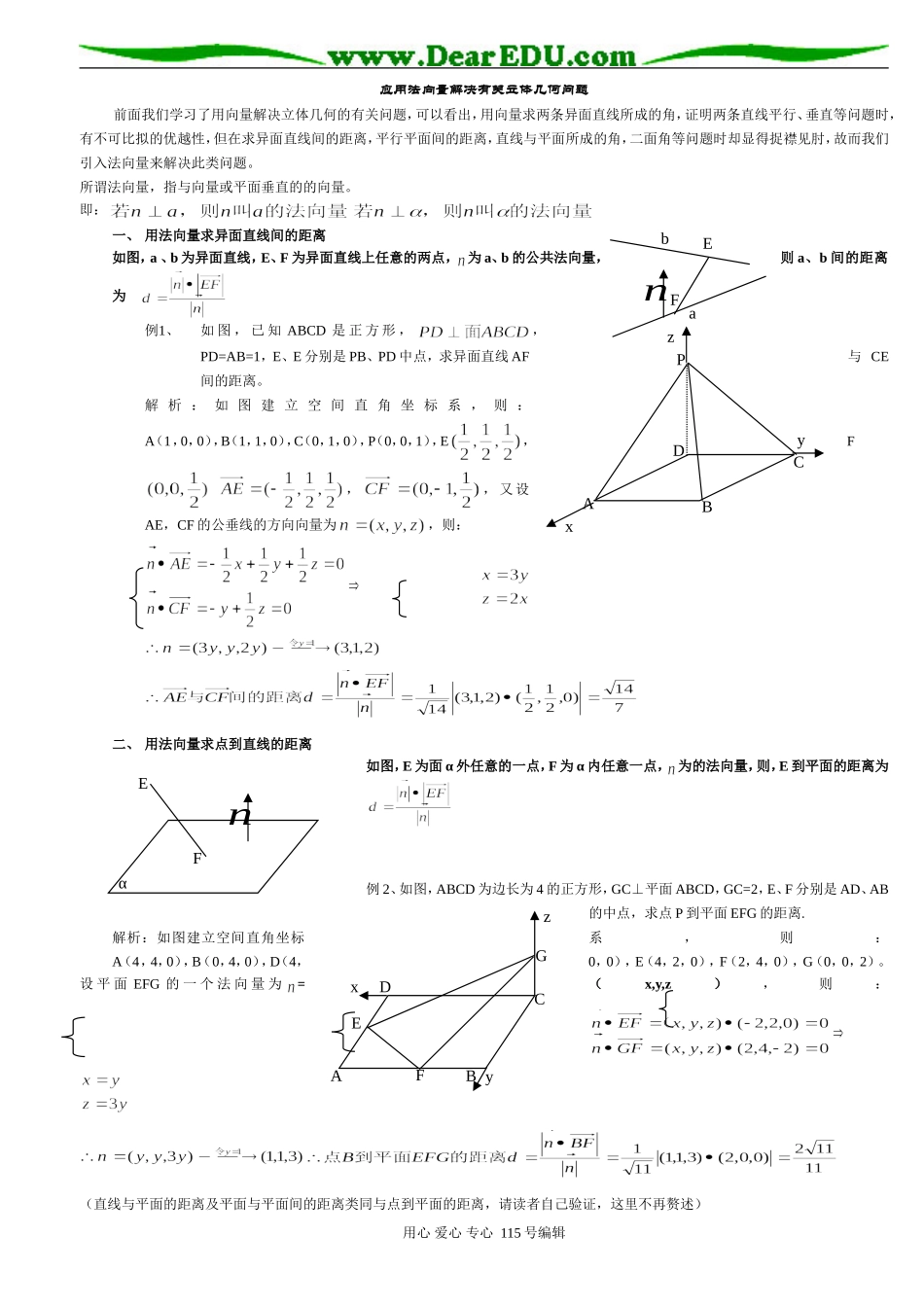
应用法向量解决有关立体几何问题前面我们学习了用向量解决立体几何的有关问题,可以看出,用向量求两条异面直线所成的角,证明两条直线平行、垂直等问题时,有不可比拟的优越性,但在求异面直线间的距离,平行平面间的距离,直线与平面所成的角,二面角等问题时却显得捉襟见肘,故而我们引入法向量来解决此类问题。所谓法向量,指与向量或平面垂直的的向量。即:一、用法向量求异面直线间的距离如图,a、b为异面直线,E、F为异面直线上任意的两点,为a、b的公共法向量,则a、b间的距离为例1、如图,已知ABCD是正方形,,PD=AB=1,E、E分别是PB、PD中点,求异面直线AF与CE间的距离。解析:如图建立空间直角坐标系,则:A(1,0,0),B(1,1,0),C(0,1,0),P(0,0,1),E,F,,又设AE,CF的公垂线的方向向量为,则:二、用法向量求点到直线的距离如图,E为面α外任意的一点,F为α内任意一点,为的法向量,则,E到平面的距离为例2、如图,ABCD为边长为4的正方形,GC⊥平面ABCD,GC=2,E、F分别是AD、AB的中点,求点P到平面EFG的距离.解析:如图建立空间直角坐标系,则:A(4,4,0),B(0,4,0),D(4,0,0),E(4,2,0),F(2,4,0),G(0,0,2)。设平面EFG的一个法向量为=(x,y,z),则:(直线与平面的距离及平面与平面间的距离类同与点到平面的距离,请读者自己验证,这里不再赘述)用心爱心专心115号编辑abFEnEFαnAPDCByzxBACDEFGyzx三、用法向量求直线与平面所成的角如图,直线EF交平面α于F,为的一个法向量,则直线EF与平面α所成的角为例3、如图,长方体ABCD-A1B1C1D1中,,E、F分别是AB,C1D1的中点,求:(1)、A1B1与面A1EF所成的角。(2)、BC1到面A1EF的距离。解:如图建立空间直角坐标系,则,A(,0,0),C(0,,0),B(,,0),C1(0,,0),D1(0,0,1),A1(,0,1),E(,,0),F(0,,1)。(1)、设平面A1EF的一个法向量为=(x,y,z),则:,故,因此,A1B1与面A1EF所成的角为。用向量法研究立体几何问题1.1、用传统方法解决立体几何问题与用向量法解决立体几何问题之比较用传统方法解决立体几何问题,通常都必须添加辅助线,并且要经过各种手段进行转化,它具有较大的灵活性,学生掌握起来比较困难。空间向量的引入,给传统的立体几何内容注入了新的活力,向量是既有大小又有方向的量,既具有图形的直观性,又有代数推理的严密性,是数形结合的一个很好的桥梁。而空间向量是处理空间问题的重要方法,通过将空间元素间的位置关系转化为数量关系,将过去的形式逻辑证明转化为数值计算,化繁难为简易,化复杂为简单,为学生处理某些立体几何问题提供了的新视角。借助空间向量这一工具,可以降低思维难度,增加了可操作性,从而减轻了学生负担,使他们对立体几何更容易产生兴趣。下面举例说明:例如图,在正方体ABCD-A1B1C1D中,E、F分别是BB1、CD的中点.(I)求AE与D1F所成的角(II)证明面AED⊥面A1FD1解:(I)取AB中点G,连结AG,FG.因为F是CD的中点,所以GF、AD平行且相等,又A1D1、AD平行且相等,所以GF、A1D1平行且相等,故GFD1A1是平行四边形,AG∥D1F.设A1G与AE相交于点H,则∠AHA1是AE与D1F所成的角,因为E是BB1的中点,所以Rt△A1AG≌Rt△ABE,∠GA1A=∠GAH,从而∠AHA1=90°,即直线AE与D1F所成角为直角.(II) AC1是正方体,∴AD⊥面DC1.又D1F面DC1,∴AD⊥D1F,由(I)知AE⊥D1F,又AD∩AE=A,所以D1F⊥面AED.用心爱心专心115号编辑FA1B1C1D1BCDAEGHEFαnzxy又因为D1F面A1FD1,所以面AED⊥面A1FD1.下边看利用向量的有关知识解答该题:证明:如右图建立空间直角坐标系:D—xyz。设正方体的棱长为2,则有A(2,0,0)、(2,0,2)D(0,0,0)、D1(0,0,2)、F(0,1,0)、E(2,2,1)(I) =(0,2,1),=(0,1,-2)∴=(0,2,1)•(0,1,-2)=0∴AED1F∴AE与D1F所成的角为90即直线AE与D1F所成角为直角.(II)设面A1ED1的一个法向量=(,,),面AED的一个法向量=(,,) •=-2=0 •=-2+-2=0∴可取=(0,2,1) •=-2=0 •=2+=0∴可取=(0,-1,2)。 •=(0,2,1)•(0,-1,2)=0,∴⊥,从而面AED⊥...