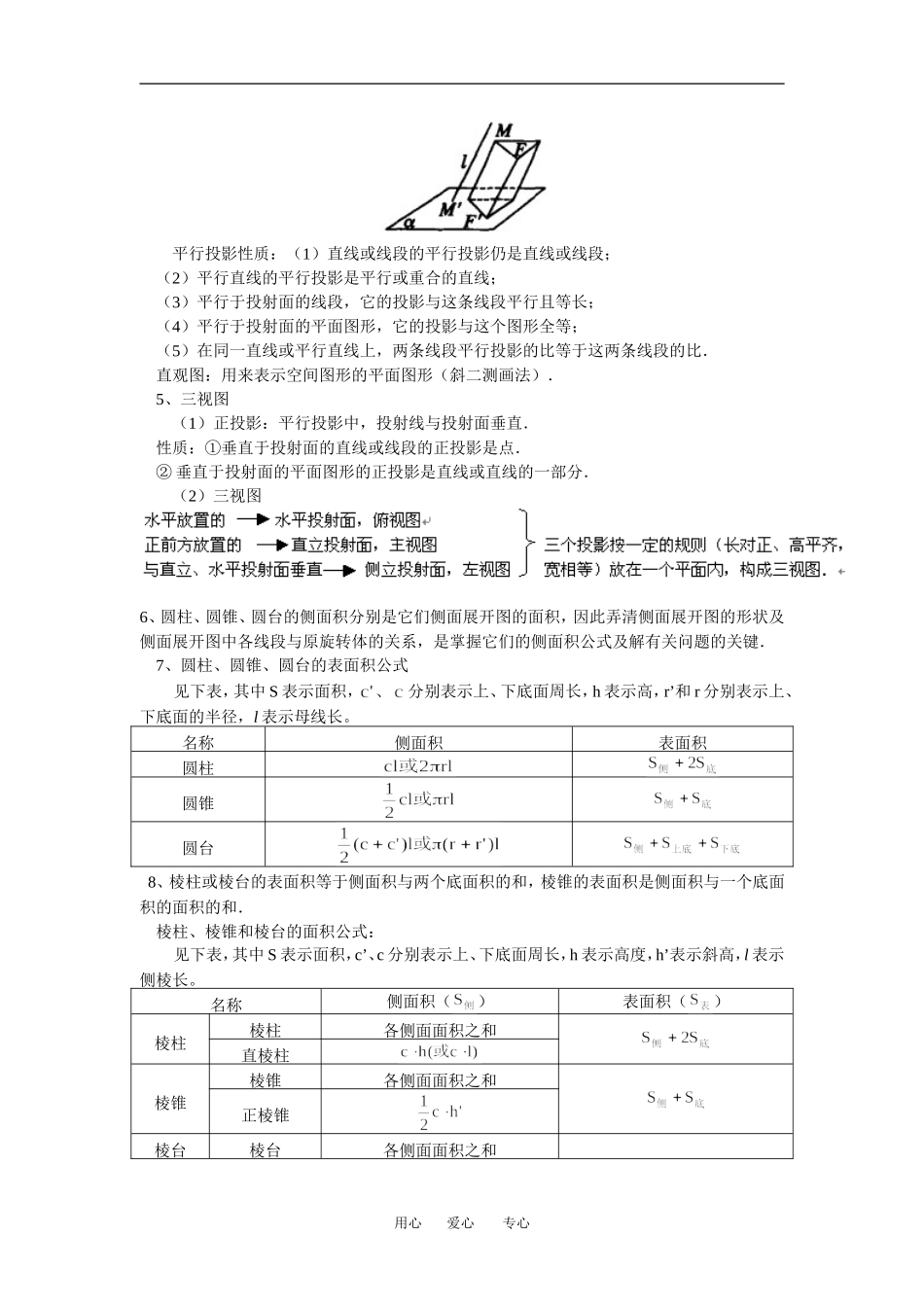
高三数学理第一轮复习:立体几何复习人教实验B版【本讲教育信息】一.教学内容:立体几何复习:1、空间几何体的结构及其三视图和直观图2、空间几何体的表面积和体积【知识梳理】1、构成空间几何体的基本元素点、线、面是构成几何体的基本元素,线有直线(段)和曲线(段)之分,面有平面(部分)和曲面(部分)之分.在立体几何中,平面是无限延展的.通常画一个平行四边形表示一个平面,用希腊字母、、、命名,也可用表示它的平行四边形的对角顶点的字母来命名,如平面ABCD或平面AC等.2、棱柱、棱锥、棱台的结构特征(1)多面体是由若干个平面多边形所围成的几何体,多边形叫做多面体的面;相邻两面公共边叫做多面体的棱,棱与棱的公共点叫做多面体的顶点.不共面两顶点的连线叫做多面体的对角线;(2)棱柱:两个面(底面)互相平行,其余每两个相邻面(侧面)的交线(侧棱)平行.分类:(3)棱锥:有一个面(底面)是多边形,其余各面(侧面)都是有一个公共点(顶点)的三角形.分类:底面多边形:三棱锥、四棱锥、五棱锥……特别地,正棱锥指底面为正多边形,水平放置时,顶点在底面投影为底面多边形的中心;(4)棱台:底面水平放置的棱锥被平行于底面的平面所截,截面(上底面)与圆锥底面(下底面)之间的部分.正棱台:正棱锥截得的棱台.3、圆柱、圆锥、圆台、球球:空间中到一个定点距离等于定长的点的集合.大圆:球面被经过球心的平面截得的圆.小圆:球面被不经过球心的平面截得的圆.球面距离:经过两点的大圆在这两点间的一段劣弧的长度.4、平行投影与直观图平行投影:(如图),图形F,直线L与a相连,过F上任一点M作直线平行FF'交平面于点,则称为M在内的关于直线L的平行投影.用心爱心专心平行投影性质:(1)直线或线段的平行投影仍是直线或线段;(2)平行直线的平行投影是平行或重合的直线;(3)平行于投射面的线段,它的投影与这条线段平行且等长;(4)平行于投射面的平面图形,它的投影与这个图形全等;(5)在同一直线或平行直线上,两条线段平行投影的比等于这两条线段的比.直观图:用来表示空间图形的平面图形(斜二测画法).5、三视图(1)正投影:平行投影中,投射线与投射面垂直.性质:①垂直于投射面的直线或线段的正投影是点.②垂直于投射面的平面图形的正投影是直线或直线的一部分.(2)三视图6、圆柱、圆锥、圆台的侧面积分别是它们侧面展开图的面积,因此弄清侧面展开图的形状及侧面展开图中各线段与原旋转体的关系,是掌握它们的侧面积公式及解有关问题的关键.7、圆柱、圆锥、圆台的表面积公式见下表,其中S表示面积,分别表示上、下底面周长,h表示高,r’和r分别表示上、下底面的半径,l表示母线长。名称侧面积表面积圆柱圆锥圆台8、棱柱或棱台的表面积等于侧面积与两个底面积的和,棱锥的表面积是侧面积与一个底面积的面积的和.棱柱、棱锥和棱台的面积公式:见下表,其中S表示面积,c’、c分别表示上、下底面周长,h表示高度,h’表示斜高,l表示侧棱长。名称侧面积()表面积()棱柱棱柱各侧面面积之和直棱柱棱锥棱锥各侧面面积之和正棱锥棱台棱台各侧面面积之和用心爱心专心正棱台9、棱柱、棱锥、棱台的体积公式其中,、是底面积,h是高。10、圆柱、圆锥、圆台的体积公式其中,、r’是底面半径,h是高。熟练掌握柱、锥、台体积公式及其内在联系是达到准确计算的关键。半径为R的球的表面积,体积.【典型例题】例1.下面是关于四棱柱的四个命题:①若有两个侧面垂直于底面,则该四棱柱为直四棱柱;②若过两个相对侧棱的截面都垂直于底面,则该四棱柱为直四棱柱;③若四个侧面两两全等,则该四棱柱为直四棱柱;④若四棱柱的四条对角线两两相等,则该四棱柱为直四棱柱。其中,真命题的编号是___________。(写出所有真命题的编号)点拨:根据学过的几何体结构特征,亦可用反例法否定命题。解析:对于①,平行六面体的两个相对侧面也可能与底面垂直且相互平行,故①假;对于②,两截面的交线平行于侧棱,且垂直于底面,故②真;对于③,作正四棱柱的两个平行菱形截面,可得满足条件的斜四棱柱(如图),故③假;对于④,四棱柱一个...