高三数学期末练习一苏教版VIP免费

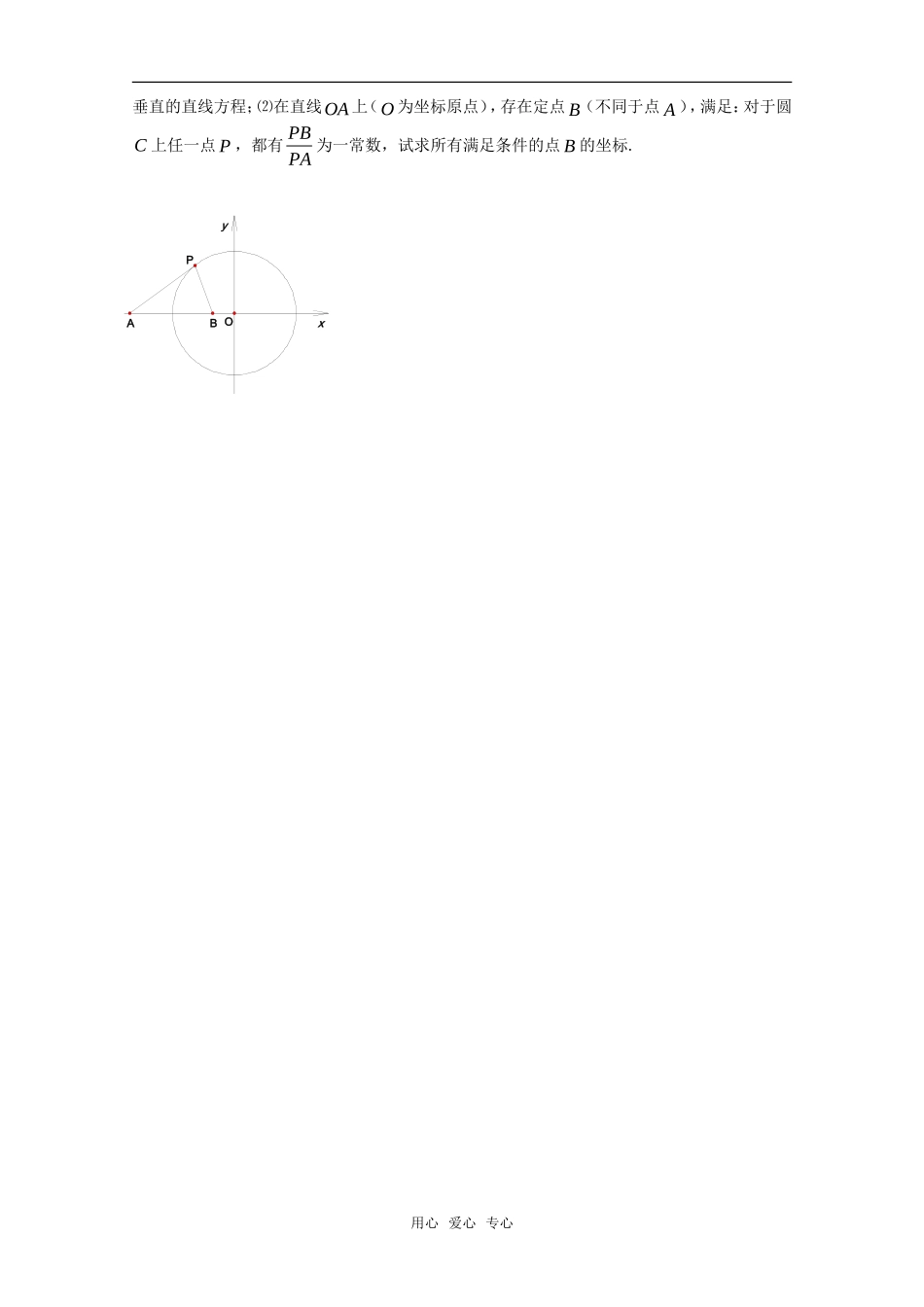
QOF2F1Pyx高三数学期末复习（一）一、填空题（本大题共14小题，每小题5分，共70分）１.已知集合},12,3,1{,,32mBmA若BA，则实数m的值为.２.若复数iiaiz(),)(2(为虚数单位）为纯虚数，则实数a的值为.３.长方形ABCD中,，AB＝2，BC＝1，O为AB的中点，在长方形ABCD内随机取一点，取到的点到O的距离大于1的概率为___________.４．.阅读下列算法语句:ReadS1ForIfrom1to5step2SS+IEndforPrintSEnd输出的结果是．５．设,ab为不重合的两条直线，,为不重合的两个平面，给出下列命题：（1）若a∥且b∥，则a∥b；（2）若a且b，则a∥b；（3）若a∥且a∥，则∥；（4）若a且a，则∥．上面命题中，所有真命题的序号是．６．如图是某学校学生体重的频率分布直方图，已知图中从左到右的前3个小组的频率之比为1:2:3，第2小组的频数为10，则抽取的学生人数是.７．若函数y=cosx(>0)在(0,2)上是单调函数，则实数的取值范围是____________.８．已知扇形的圆心角为2（定值），半径为R（定值），分别按图一、二作扇形的内接矩形，若按图一作出的矩形面积的最大值为21tan2R，则按图二作出的矩形面积的最大值为.９．已知点P在直线x+2y-1=0上，点Q在直线x+2y+3=0上，PQ的中点为M（x0，y0），且y0>x0+2，则00yx的取值范围为。10．如图，已知12,FF是椭圆2222:1xyCab(0)ab的左、右焦点，点P在椭圆C上，线段2PF与圆222xyb相切于点Q，且点Q为线段2PF的中点，则椭圆C的离心率为.11．等腰三角形ABC的腰AC上的中线BD的长为3，则△ABC的面积的最大值为.用心爱心专心22图一第8题图图二12．给定正整数)2(nn按右图方式构成三角形数表：第一行依次写上数1，2，3，……n，在下面一行的每相邻两个数的正中间上方写上这两个数之和，得到上面一行的数（比下一行少一个数），依次类推，最后一行（第n行）只有一一个数.例如n=6时数表如图所示，则当n=2010时最后一行的数是.13．已知函数是定义在(0,)上的单调增函数，当nN时，()fnN，若[()]3ffnn，则f(5)的值等于。14．已知f(x)=ax2+bx+c(a≠0)，g(x)=f[f(x)]，其中真命题的个数是_________个。①若f(x)无零点，则g(x)>0对x∈R成立；②若f(x)有且只有一个零点，则g(x)必有两个零点；③若方程f(x)=0有两个不等实根，则方程g(x)=0不可能无解。[来源:Z#xx#k.Com]二、解答题15.已知O为坐标原点，2(2sin,1),(1,23sincos1)OAxOBxx�，()fxOAOBm�（Ⅰ）求)(xfy的单调递增区间；（Ⅱ）若)(xf的定义域为[,]2，值域为[2,5]，求m的值.16．(14分)在四棱锥P－ABCD中，∠ABC＝∠ACD＝90°，∠BAC＝∠CAD＝60°，PA⊥平面ABCD，E为PD的中点，PA＝2AB＝2．（Ⅰ）求四棱锥P－ABCD的体积V；（Ⅱ）若F为PC的中点，求证PC⊥平面AEF；（Ⅲ）求证CE∥平面PAB．17.如图，灌溉渠的横截面是等腰梯形，底宽2米，边坡的长为x米、倾角为锐角.(1)当3且灌溉渠的横截面面积大于8平方米时，求x的最小正整数值；(2)当x=2时，试求灌溉渠的横截面面积的最大值.18.已知圆22:9Cxy，点(5,0)A，直线:20lxy.⑴求与圆C相切，且与直线l用心爱心专心PABCDEFx垂直的直线方程；⑵在直线OA上（O为坐标原点），存在定点B（不同于点A），满足：对于圆C上任一点P，都有PBPA为一常数，试求所有满足条件的点B的坐标.用心爱心专心xyOAPB19．已知无穷数列{an}中，a1，a2，…，am是首项为10，公差为－2的等差数列；am＋1，am＋2，…，a2m是首项为12，公比为12的等比数列（其中m≥3，m∈N*），并对任意的n∈N*，均有an＋2m＝an成立．（1）当m＝12时，求a2010；（2）若a52＝1128，试求m的值；（3）判断是否存在m（m≥3，m∈N*），使得S128m＋3≥2010成立？若存在，试求出m的值；若不存在，请说明理由．[来源:Z.xx.k.Com]20．已知12()|31|,()|39|(0),xxfxfxaaxR,且112212(),()()()(),()()fxfxfxfxfxfxfx.(Ⅰ)当1a时,求()fx在1x处的切线方程；(Ⅱ)当29a时,设2()()fxfx所对应的自变量取值区间的长度为l(闭区间[,]mn的长度定义为nm),试求l的最大值；(...