高三数学文立体几何、平面与平面位置关系人教版知识精讲VIP免费

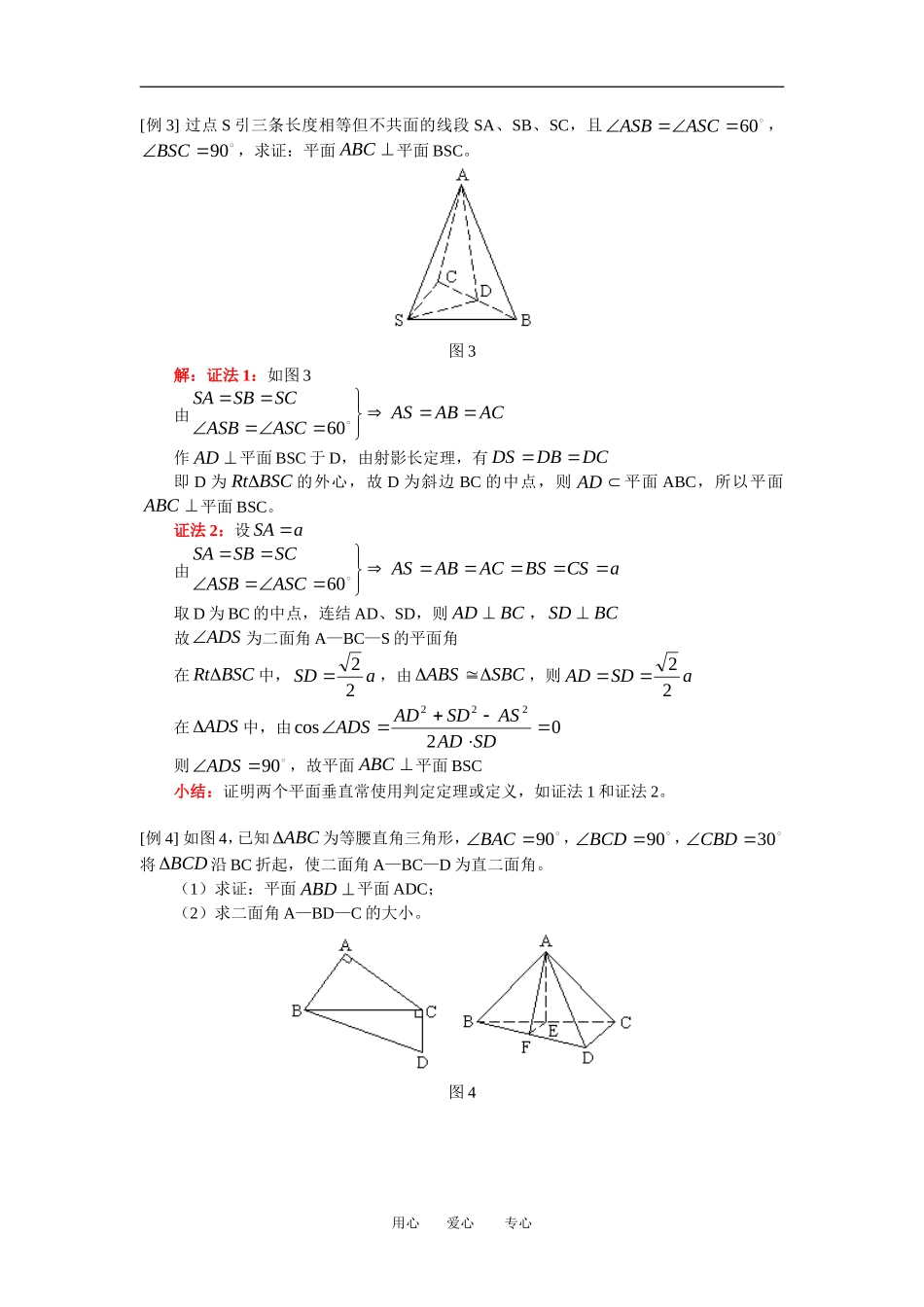
【同步教育信息】一.本周教学内容：立体几何、平面与平面位置关系二.知识结构：三.难点：1.两个平面平行、垂直的判定定理和性质定理及其应用。2.求二面角的平面角。3.异面直线上两点间距离公式。二面角是从一条直线出发的两个半平面所组成的图形，二面角的平面角是以棱上任意一点为端点，在两个面内分别作垂直于棱的两条射线，这两条射线所成的角二面角是一个空间概念，而二面角的平面角是一个平面概念。二面角是通过它的平面角来度量的。二面角的平面角是多少度，就称二面角是多少度，二面角的取值范围是],0(。书中给出了异面直线上两点间距离公式cos2222mnnmdEF由此可知dEF，因此，两条异面直线的距离，是分布在两条异面直线上的两点的距离中的最小的。【典型例题】[例1]如图1，ABCD两对角线AC与BD交于点O，过O的线段PQ恰被平面ABCD垂直平分，E、G分别是PB、QA的中点，求证：平面ADE//平面BGC。图1解：由PQ与AC垂直平分，则四边形PAQC为菱形，则AQPC//用心爱心专心又由E、G分别为PB、AQ中点，则GACF//故四边形AGCF为平行四边形，则GCAF//在平行四边形ABCD中，BCAD//故平面ADE//平面BGC小结：两个平面平行的判定定理是两个平面平行的基本方法，此外，还可以利用以下方法判定面面平行：（1）如果两个平面都与同一条直线垂直，则这两个平面平行；（2）如果两个平面都与同一个平面平行，则这两个平面平行。[例2]已知长方体ABCD—A1B1C1D1中，aAA1，bAB，cAD。（1）证明：平面AB1C//平面A1C1D；（2）求平面AB1C与平面A1C1D的距离。图2解：（1）如图2所示 DCBA//11∴四边形A1B1CD为∴B1C//A1D同理AB1//C1D∴平面AB1C//平面A1C1D（2）设平面AB1C与平面A1C1D的距离为d，由面面距离的定义知，点D到平面AB1C的距离即等于平面AB1C与平面A1C1D的距离d，又由平面AB1C过线段DB的中点O，则点B和D到平面AB1C的距离相等，以下利用体积变换求点B到平面AB1C的距离d作ACBE于E，连结B1E，由三垂线定理ACEB1在ABCRt中，22cbbcACBCABBE在BEBRt1中，222222222211cbaccbbaBEBBEB故222222121211accbbaEBACSCAB由三棱锥B—AB1C与三棱锥B1—ABC为同一四面体，则BBSdSABCCAB131311222222accbbaabcd即平面AB1C与平面A1C1D的体积为222222accbbaabc小结：（1）面面距离、线面距离都可以转化为点面距离，而点面距离除直接求垂线段长外，还可以利用间接法，如本例使用体积变换求得。（2）易证如果两条异面直线分别位于两个互相平行的平面内，则这两个平面的距离与异面直线的距离相等，利用这个事实，我们可以把求异面直线的距离转化为求两个平面的距离，如本例异面直线AB1与A1C1的距离与这两个平行平面距离相等。用心爱心专心[例3]过点S引三条长度相等但不共面的线段SA、SB、SC，且60ASCASB，90BSC，求证：平面ABC平面BSC。图3解：证法1：如图3由ACABASASCASBSCSBSA60作AD平面BSC于D，由射影长定理，有DCDBDS即D为BSCRt的外心，故D为斜边BC的中点，则AD平面ABC，所以平面ABC平面BSC。证法2：设aSA由aCSBSACABASASCASBSCSBSA60取D为BC的中点，连结AD、SD，则BCAD，BCSD故ADS为二面角A—BC—S的平面角在BSCRt中，aSD22，由SBCABS，则aSDAD22在ADS中，由02cos222SDADASSDADADS则90ADS，故平面ABC平面BSC小结：证明两个平面垂直常使用判定定理或定义，如证法1和证法2。[例4]如图4，已知ABC为等腰直角三角形，90BAC，90BCD，30CBD将BCD沿BC折起，使二面角A—BC—D为直二面角。（1）求证：平面ABD平面ADC；（2）求二面角A—BD—C的大小。图4用心爱心专心解：（1）由ABCABABCDCBCDBCABCDBCDCBCDCDBCABC平面平面平面平面平面平面平面又由ACABABDCADCABDABDABADCAB平面平面平面平面（2）作BCAE于E，则E为等腰ABCRt的中点，过E作BDEF于F，连结AF。由BDAFBDEFDBCAEBCDBCABCABCAEBCAEDBCABC...