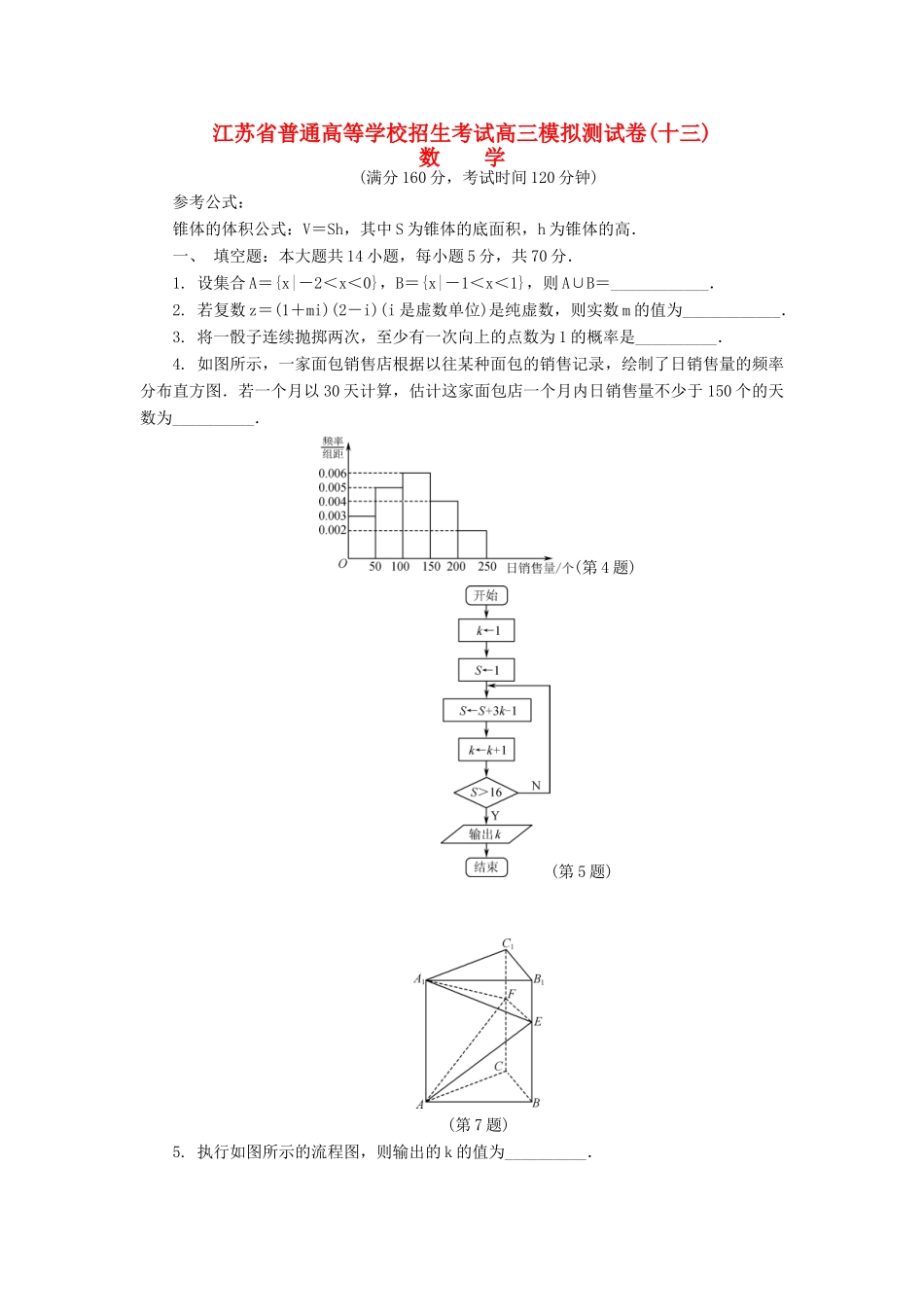
江苏省普通高等学校招生考试高三模拟测试卷(十三)数学(满分160分,考试时间120分钟)参考公式:锥体的体积公式:V=Sh,其中S为锥体的底面积,h为锥体的高.一、填空题:本大题共14小题,每小题5分,共70分.1.设集合A={x|-2<x<0},B={x|-1<x<1},则A∪B=____________.2.若复数z=(1+mi)(2-i)(i是虚数单位)是纯虚数,则实数m的值为____________.3.将一骰子连续抛掷两次,至少有一次向上的点数为1的概率是__________.4.如图所示,一家面包销售店根据以往某种面包的销售记录,绘制了日销售量的频率分布直方图.若一个月以30天计算,估计这家面包店一个月内日销售量不少于150个的天数为__________.(第4题)(第5题)(第7题)5.执行如图所示的流程图,则输出的k的值为__________.6.设公差不为0的等差数列{an}的前n项和为Sn.若S3=a,且S1,S2,S4成等比数列,则a10=______________.7.如图,正三棱柱ABCA1B1C1中,AB=4,AA1=6.若E,F分别是棱BB1,CC1上的点,则三棱锥AA1EF的体积是____________.8.已知函数f(x)=2sin(ωx+φ)的最小正周期为π,且它的图象过点,则φ的值为__________.9.已知函数f(x)=则不等式f(x)≥-1的解集是________.10.在平面直角坐标系xOy中,抛物线y2=2px(p>0)的焦点为F,双曲线-=1(a>0,b>0)的两条渐近线分别与抛物线交于A,B两点(A,B异于坐标原点O).若直线AB恰好过点F,则双曲线的渐近线方程是____________.11.在△ABC中,A=120°,AB=4.若点D在边BC上,且BD=2DC,AD=,则AC的长为____________.12.已知圆O:x2+y2=1,圆M:(x-a)2+(y-a+4)2=1.若圆M上存在点P,过点P作圆O的两条切线,切点为A,B,使得∠APB=60°,则实数a的取值范围为____________.13.已知函数f(x)=ax2+x-b(a,b均为正数),不等式f(x)>0的解集记为P,集合Q={x|-2-t<x<-2+t}.若对于任意正数t,P∩Q≠,则-的最大值是__________.14.若存在两个正实数x、y,使得等式x+a(y-2ex)(lny-lnx)=0成立,其中e为自然对数的底数,则实数a的取值范围为__________.二、解答题:本大题共6小题,共90分.解答时应写出必要的文字说明、证明过程或演算步骤.15.(本小题满分14分)已知α为锐角,cos=.求:(1)tan的值;(2)sin的值.16.(本小题满分14分)如图,在三棱锥PABC中,平面PAB⊥平面ABC,PA⊥PB,M、N分别为AB、PA的中点.(1)求证:PB∥平面MNC;(2)若AC=BC,求证:PA⊥平面MNC.17.(本小题满分14分)如图,某城市有一块半径为1(单位:百米)的圆形景观,圆心为C,有两条与圆形景观相切且互相垂直的道路.最初规划在拐角处(图中阴影部分)只有一块绿化地,后来有众多市民建议在绿化地上建一条小路,便于市民快捷地往返两条道路.规划部门采纳了此建议决定在绿化地中增建一条与圆C相切的小道AB.问:A,B两点应选在何处可使得小道AB最短?18.(本小题满分16分)在平面直角坐标系xOy中,点C在椭圆M:+=1(a>b>0)上.若点A(-a,0),B(0,),且AB=BC.(1)求椭圆M的离心率;(2)设椭圆M的焦距为4,P,Q是椭圆M上不同的两点,线段PQ的垂直平分线为直线l,且直线l不与y轴重合.①若点P(-3,0),直线l过点,求直线l的方程;②若直线l过点(0,-1),且与x轴的交点为D,求D点横坐标的取值范围.19.(本小题满分16分)对于函数f(x),在给定区间[a,b]内任取n+1(n≥2,n∈N*)个数x0,x1,x2,…,xn,使得a=x0<x1<x2<…<xn-1<xn=b,记S=|f(xi+1)-f(xi)|.若存在与n及xi(i≤n,i∈N)均无关的正数A,使得S≤A恒成立,则称f(x)在区间[a,b]上具有性质V.(1)若函数f(x)=-2x+1,给定区间为[-1,1],求S的值;(2)若函数f(x)=,给定区间为[0,2],求S的最大值;(3)对于给定的实数k,求证:函数f(x)=klnx-x2在区间[1,e]上具有性质V.20.(本小题满分16分)已知数列{an}的前n项和为Sn,且对任意正整数n都有an=(-1)nSn+pn(p为常数,p≠0).(1)求p的值;(2)求数列{an}的通项公式;(3)设集合An={a2n-1,a2n},且bn,cn∈An,记数列{nbn},{ncn}的前n项和分别为Pn,Qn.若b1≠c1,求证:对任意n∈N*,Pn≠Qn.(十三)1.{x|-2<x<1}解析:本题主要考查集...