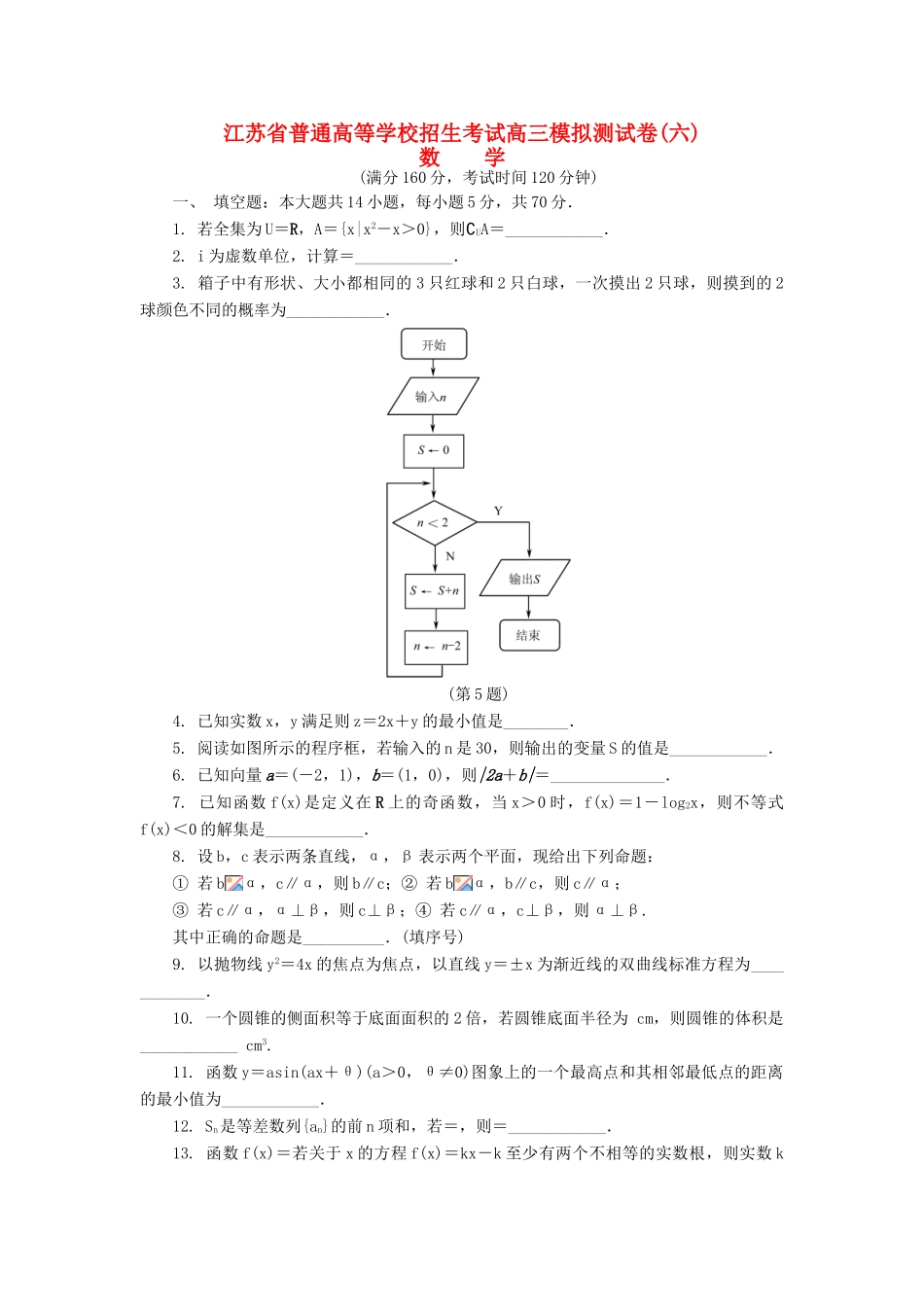
江苏省普通高等学校招生考试高三模拟测试卷(六)数学(满分160分,考试时间120分钟)一、填空题:本大题共14小题,每小题5分,共70分.1.若全集为U=R,A={x|x2-x>0},则∁UA=____________.2.i为虚数单位,计算=____________.3.箱子中有形状、大小都相同的3只红球和2只白球,一次摸出2只球,则摸到的2球颜色不同的概率为____________.(第5题)4.已知实数x,y满足则z=2x+y的最小值是________.5.阅读如图所示的程序框,若输入的n是30,则输出的变量S的值是____________.6.已知向量a=(-2,1),b=(1,0),则|2a+b|=______________.7.已知函数f(x)是定义在R上的奇函数,当x>0时,f(x)=1-log2x,则不等式f(x)<0的解集是____________.8.设b,c表示两条直线,α,β表示两个平面,现给出下列命题:①若bα,c∥α,则b∥c;②若bα,b∥c,则c∥α;③若c∥α,α⊥β,则c⊥β;④若c∥α,c⊥β,则α⊥β.其中正确的命题是__________.(填序号)9.以抛物线y2=4x的焦点为焦点,以直线y=±x为渐近线的双曲线标准方程为____________.10.一个圆锥的侧面积等于底面面积的2倍,若圆锥底面半径为cm,则圆锥的体积是____________cm3.11.函数y=asin(ax+θ)(a>0,θ≠0)图象上的一个最高点和其相邻最低点的距离的最小值为____________.12.Sn是等差数列{an}的前n项和,若=,则=____________.13.函数f(x)=若关于x的方程f(x)=kx-k至少有两个不相等的实数根,则实数k的取值范围为____________.14.由sin36°=cos54°,可求得cos2016°的值为____________.二、解答题:本大题共6小题,共90分.解答时应写出必要的文字说明、证明过程或演算步骤.15.(本小题满分14分)如图,四棱锥PABCD中,PD=PC,底面ABCD是直角梯形,AB⊥BC,AB∥CD,CD=2AB,点M是CD的中点.求证:(1)AM∥平面PBC;(2)CD⊥PA.16.(本小题满分14分)在△ABC中,角A,B,C所对应的边分别是a,b,c,向量m=(a-c,b+c),n=(b-c,a),且m∥n.(1)求B;(2)若b=,cos=,求a.17.(本小题满分14分)如图,某工业园区是半径为10km的圆形区域,离园区中心O点5km处有一中转站P,现准备在园区内修建一条笔直公路AB经过中转站,公路AB把园区分成两个区域.(1)设中心O对公路AB的视角为α,求α的最小值,并求较小区域面积的最小值;(2)为方便交通,准备过中转站P在园区内再修建一条与AB垂直的笔直公路CD,求两条公路长度和的最小值.18.(本小题满分16分)已知在平面直角坐标系xOy中,椭圆+=1(a>b>0)的离心率为,左顶点为A(-3,0),圆心在原点的圆O与椭圆的内接△AEF的三条边都相切.(1)求椭圆方程;(2)求圆O方程;(3)B为椭圆的上顶点,过B作圆O的两条切线,分别交椭圆于M,N两点,试判断并证明直线MN与圆O的位置关系.19.(本小题满分16分)已知数列{an}的各项都为自然数,前n项和为Sn,且存在整数λ,使得对任意正整数n都有Sn=(1+λ)an-λ恒成立.(1)求λ值,使得数列{an}为等差数列,并求数列{an}的通项公式;(2)若数列{an}为等比数列,此时存在正整数k,当1≤k<j时,有i=2016,求k.20.(本小题满分16分)已知函数f(x)=[ax2-(2a+1)x+2a+1]ex.(1)求函数f(x)的单调区间;(2)设x>0,2a∈[3,m+1],f(x)≥b2a-1e恒成立,求正数b的范围.(六)1.[0,1]解析:∁UA={x|x2-x≤0}=[0,1].本题考查集合补集的概念及一元二次不等式的解法,属于容易题.2.-i解析:==-i.本题主要考查复数的概念及四则运算等基础知识,属于容易题.3.解析:由5只球中一次摸出2只球,共有10种摸法,摸到的2只球颜色不同的摸法共有6种,则所求的概率为.本题考查用列举法解决古典概型问题,属于容易题.4.1解析:作出可行域发现最优解为(1,-1),则目标函数z=2x+y的最小值为1.本题考查线性规划解决最值问题,属于容易题.5.240解析:n=30时,S=30;n=28时,S=30+28;n=26时,S=30+28+26;以此类推,n=2时,S=30+28+26+……+2=240.本题考查流程图基础知识,关键是把握好每一次循环体的执行情况.本题属于容易题.6.解析:2a+b=(-3,2),则|2a+b|=.本题考查向量的坐标运算,以及利用平方法求模.本题...