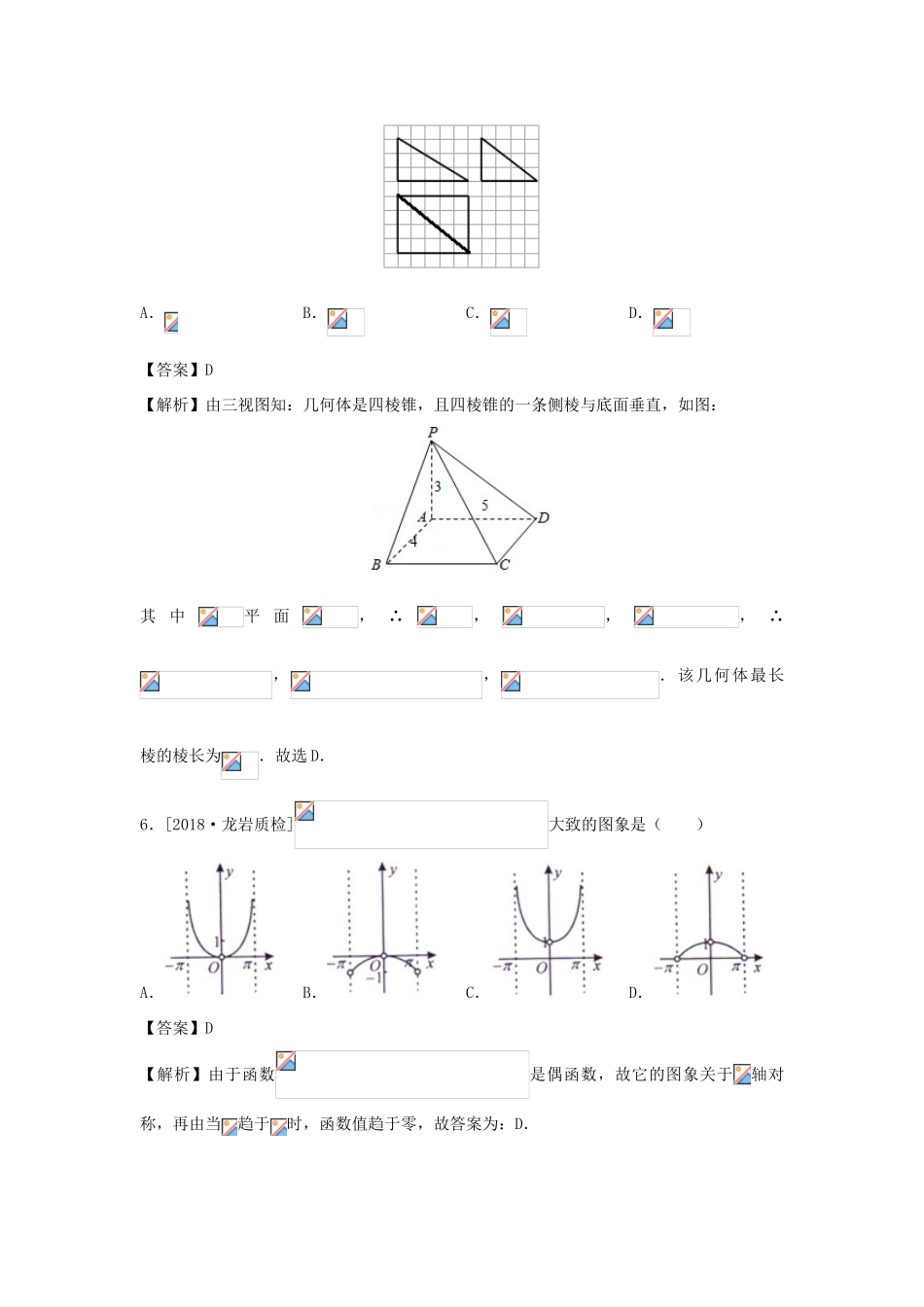
河南省淮滨高级中学2018届高三数学下学期第二次模拟仿真卷(四)文注意事项:1.答题前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。2.选择题的作答:每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,写在试题卷、草稿纸和答题卡上的非答题区域均无效。3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。写在试题卷、草稿纸和答题卡上的非答题区域均无效。4.考试结束后,请将本试题卷和答题卡一并上交。第Ⅰ卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.[2018·太原期末]已知,都是实数,那么“”是“”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】D【解析】:,:,与没有包含关系,故为“既不充分也不必要条件”.故选D.2.[2018·豫南九校]抛物线的焦点坐标为()A.B.C.D.【答案】B【解析】化为标准方程得,故焦点坐标为.故选B.3.[2018·南山中学]下列4个图从左到右位次是四位同学甲、乙、丙、丁的五能评价雷达图:甲乙丙丁在从他们四人中选一位发展较全面的学生,则应该选择()A.甲B.乙C.丙D.丁【答案】B【解析】通过雷达图不难发现乙同学没有偏弱,发展比较全面,其余同学都有不足的地方故选B.4.[2018·行知中学]设,满足约束条件,则目标函数的最小值为()A.B.C.D.【答案】A【解析】如图,过时,取最小值,为.故选A.5.[2018·三门峡期末]《九章算术》是我国古代内容极为丰富的数学名著,系统地总结了战国、秦、汉时期的数学成就.书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为“阳马”,若某“阳马”的三视图如图所示(网格纸上小正方形的边长为1),则该“阳马”最长的棱长为()A.B.C.D.【答案】D【解析】由三视图知:几何体是四棱锥,且四棱锥的一条侧棱与底面垂直,如图:其中平面,∴,,,∴,,.该几何体最长棱的棱长为.故选D.6.[2018·龙岩质检]大致的图象是()A.B.C.D.【答案】D【解析】由于函数是偶函数,故它的图象关于轴对称,再由当趋于时,函数值趋于零,故答案为:D.7.[2018·深圳一模]函数(,是常数,,)的部分图象如图所示,为得到函数,只需将函数的图象()A.向左平移个长度单位B.向右平移个长度单位C.向左平移个长度单位D.向右平移个长度单位【答案】A【解析】由图象可得,,,则,时,,时,可得,,将向左平移个单位,可得,所以为得到函数,只需将函数的图象向左平移个长度单位,故选A.8.[2018·三门峡期末]运行如图所示的程序框图,设输出数据构成的集合为,从集合中任取一个元素,则函数,是增函数的概率为()A.B.C.D.【答案】A【解析】由框图可知,其中基本事件的总数为5,设集合中满足“函数,是增函数”为事件E,当函数,是增函数时,,事件E包含基本事件的个数为3,则.故选:A.9.[2018·集宁一中]已知函数(,)在处取得极小值,则的最小值为()A.4B.5C.9D.10【答案】C【解析】由,得,则,所以,所以,当且仅当,即,时等号成立,故选C.10.[2018·天一大联考]在四面体中,若,,,则四面体的外接球的表面积为()A.B.C.D.【答案】C【解析】如图所示,该四面体的四个顶点为长方体的四个顶点,设长、宽、高分别为,,,则,三式相加得:,所以该四面体的外接球直径为长方体的体对角线长,故外接球体积为:.11.[2018·凯里一中]已知的前项和为,且,,成等差数列,,数列的前项和为,则满足的最小正整数的值为()A.8B.9C.10D.11【答案】C【解析】,当时,,由,,成等差数列可得,即,解得,故,则,故,由得,即,则,即,故的最小值为.12.[2018·晋中调研]已知不等式在上恒成立,且函数在上单调递增,则实数的取值范围为()A.B.C.D.【答案】B【解析】不等式在上恒成立,令,,由图可知,或,即;又在上单调递增,故在上恒成立,,综上,.故选:B.第Ⅱ卷二、填空题:本大题共4小题,每小题5分.13.[2018·天津期末]已知为虚数单位,则__________.【答案】【解析...