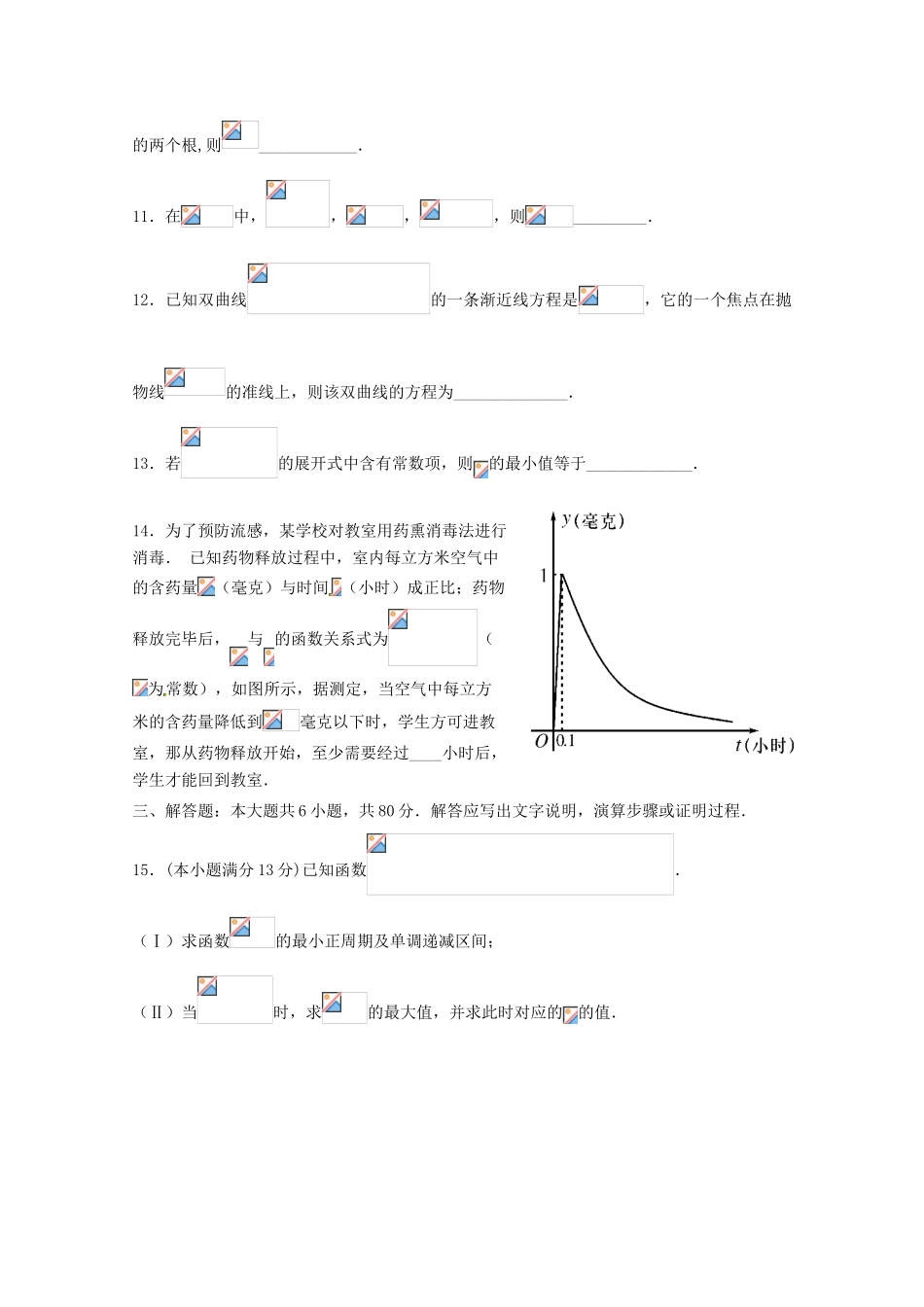
北京市第八十中学2016届高三零模综合练习高三数学(理)(考试时间120分钟,满分150分)本试卷分为选择题(共40分)和非选择题(共110分)两部分第一部分(选择题共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,选出符合题目要求的一项.1.已知集合,则A.B.C.D.2.下列函数中,既是奇函数又在区间上单调递增的函数为A.B.C.D.3.复数(为虚数单位)在复平面内对应点的坐标是A.B.C.D.4.若几何体的三视图如图所示,则该几何体的体积为A.B.C.D.5.已知,是实数,则“”是“”的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件6.执行如图的程序框图,则输出的值为A.B.C.D.7.已知非零向量,满足,且与的夹角为,则的取值范围是A.B.C.D.8.函数是定义在R上的偶函数,且满足,当时,,若方程恰有三个不相等的实数根,则实数的取值范围是A.B.C.D.第二部分(非选择题共110分)二、填空题:本大题共6小题,每小题5分,共30分.把答案填在答题卡上.9.已知变量满足,则的最大值为_______10.已知等比数列是递增数列,是的前项和,若是方程的两个根,则____________.11.在中,,,,则_________.12.已知双曲线的一条渐近线方程是,它的一个焦点在抛物线的准线上,则该双曲线的方程为______________.13.若的展开式中含有常数项,则的最小值等于_____________.14.为了预防流感,某学校对教室用药熏消毒法进行消毒.已知药物释放过程中,室内每立方米空气中的含药量(毫克)与时间(小时)成正比;药物释放完毕后,与的函数关系式为(为常数),如图所示,据测定,当空气中每立方米的含药量降低到毫克以下时,学生方可进教室,那从药物释放开始,至少需要经过____小时后,学生才能回到教室.三、解答题:本大题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.15.(本小题满分13分)已知函数.(Ⅰ)求函数的最小正周期及单调递减区间;(Ⅱ)当时,求的最大值,并求此时对应的的值.16.(本小题满分14分)直三棱柱中,,,分别是、的中点,,为棱上的点.(Ⅰ)证明:;(Ⅱ)是否存在一点,使得平面与平面所成锐二面角的余弦值为?若存在,说明点D的位置,若不存在,说明理由.17.(本小题满分13分)十八届四中全会明确提出“以法治手段推进生态文明建设”,为响应号召,北京市某小区的环保人士向该市政府部门提议“在全市范围内禁放烟花、炮竹”.为此,此小区的环保人士对该小区年龄在[15,75)的市民进行问卷调查,随机抽查了50人,并将调查情况进行整理后制成下表:年龄(岁)[15,25)[25,35)[35,45)[45,55)[55,65)[65,75)频数610121255赞成人数3610643(Ⅰ)请估计此小区年龄在[15,75)的市民对“禁放烟花、炮竹”的赞成率和被调查者的年龄平均值;(Ⅱ)若从年龄在[55,65)、[65,75)的被调查者中各随机选取两人进行追踪调查,记被选4人中不赞成“禁放烟花、炮竹”的人数为,求随机变量的分布列和数学期望.18.(本小题满分13分)已知函数.(Ⅰ)若,求函数的极值;(Ⅱ)若在有唯一的零点,求的取值范围;(Ⅲ)若,设,求证:在内有唯一的零点,且对(Ⅱ)中的,满足.19.(本小题满分14分)已知椭圆的长轴的一个端点是抛物线的焦点,离心率是.(Ⅰ)求椭圆的标准方程;(Ⅱ)已知动直线与椭圆相交于两点,且在轴上存在点,使得与的取值无关,试求点的坐标.20.(本小题满分13分)对于任意的,记集合,.若集合满足下列条件:①;②,且,不存在,使,则称具有性质.如当时,,.,且,不存在,使,所以具有性质.(Ⅰ)写出集合中的元素个数,并判断是否具有性质.(Ⅱ)证明:不存在具有性质,且,使.(Ⅲ)若存在具有性质,且,使,求的最大值.