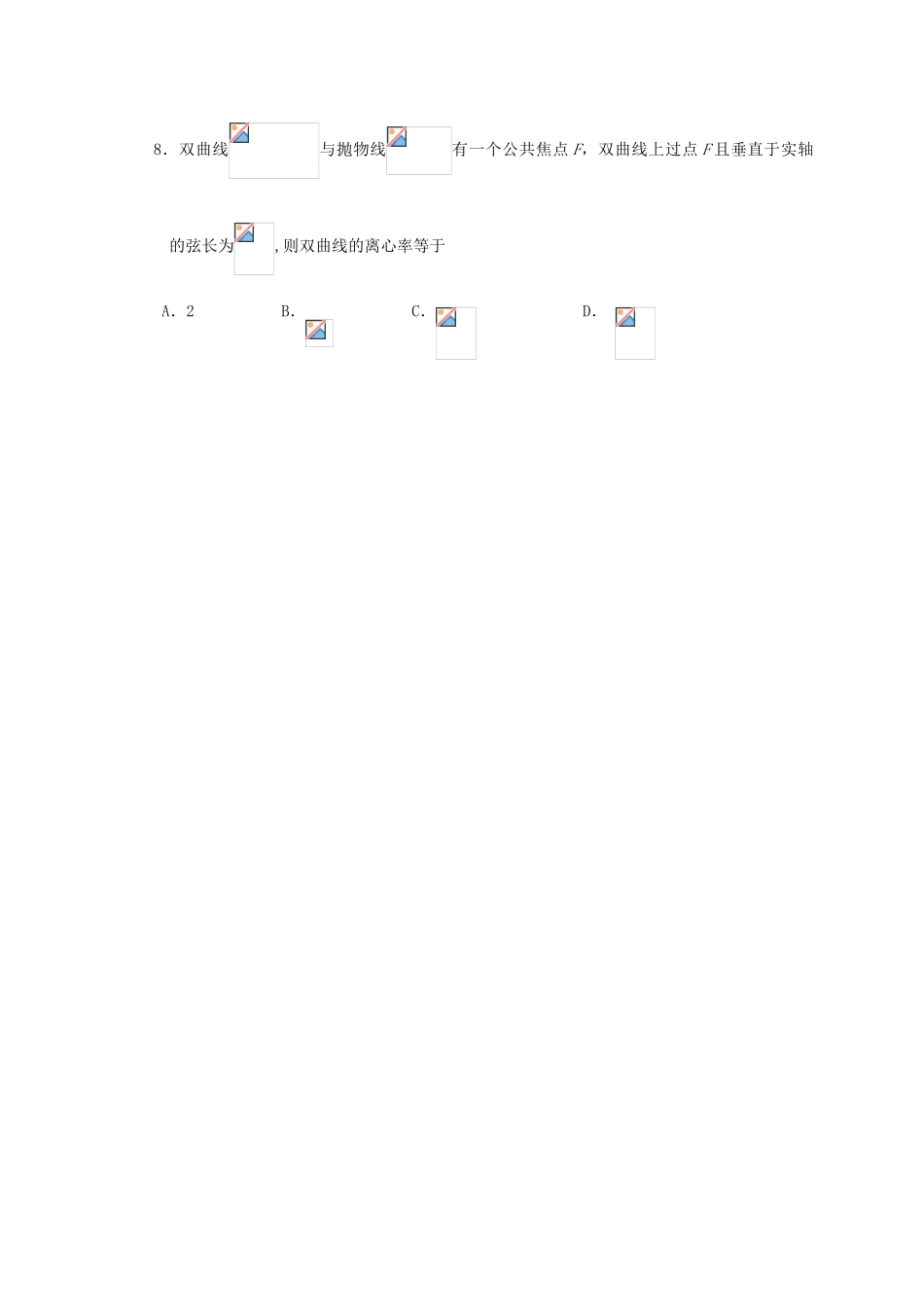
天津市红桥区重点中学2016届高三数学下学期八校联考试题理本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分150分,考试时间120分钟第Ⅰ卷(选择题共40分)一.选择题(本大题共8小题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的,请将答案填涂在答题卡上)1.复数的共轭复数等于()A.B.C.D.2.若,且,则的最小值等于()A.0B.3C.1D.-13.给出如图所示的程序框图,那么输出的数是A.7203B.7500C.7800D.74064.设,则“”是“且”的()A..充分非必要条件B.必要非充分条件C.充要条件D.既非充分也非必要条件5.的展开式中的常数项为()A.B.C.D.6.下列函数中,在区间上为增函数的是()A.B.C.D.7.在等差数列中,,且,则前项和中最大的是()A.B.C.D.8.双曲线与抛物线有一个公共焦点F,双曲线上过点F且垂直于实轴的弦长为,则双曲线的离心率等于A.2B.C.D.MOAPBC第Ⅱ卷(非选择性试题共110分)二.填空题(本大题共6小题,每小题5分,共30分,请将答案填在答题纸上)9.设集合,,则10.已知直线切⊙于点,是⊙的一条割线,如图所示有,若,则11.在中,内角所对的边分别是.若,,则的面积是12.直线l过抛物线C:x2=4y的焦点且与y轴垂直,则l与C所围成的图形的面积等于13.已知棱长为的正四面体的各顶点均在同一个球面上,则该球的体积为14.在边长为1的等边中,为上一点,且,为上一点,且满足,则取最小值时,________.三.解答题(本大题共6小题,共80分。解答应写出文字说明、证明过程或演算步骤,并将答案写在答题纸上)15(本小题满分13分)已知函数.(I)求的最小正周期和最大值;(II)讨论在上的单调性.16(本小题满分13分)某市两所中学的学生组队参加辩论赛,中学推荐了3名男生、2名女生,中学推荐了3名男生、4名女生,两校所推荐的学生一起参加集训.由于集训后队员水平相当,从参加集训的男生中随机抽取3人、女生中随机抽取3人组成代表队.(1)求A中学至少有1名学生入选代表队的概率;(2)某场比赛前,从代表队的6名队员中随机抽取4人参赛,设表示参赛的男生人数,求的分布列和数学期望.17.(本小题满分13分)在四棱锥中,底面是直角梯形,//,,平面平面。(1)求证:平面;(2)求平面与平面所成的锐二面角的大小;(3)在棱上是否存在点使得//平面?若存在,求的值;若不存在,请说明理由。18.(本小题满分13分)设数列的前项和为.已知.(I)求的通项公式;(II)若数列满足,求的前项和.19.(本小题满分14分)已知椭圆经过点,离心率为,左右焦点分别为.(Ⅰ)求椭圆的方程;(Ⅱ)若直线与椭圆交于两点,与以为直径的圆交于两点,且满足,求直线的方程.20.(本小题满分14分)第17题图设函数(为常数,是自然对数的底数).(Ⅰ)当时,求函数的单调区间;(Ⅱ)若函数在内存在两个极值点,求的取值范围.高三年级八校联考理科数学答题纸(2016.4)二.填空题910.11.12.13.14..三.解答题15(I)(2)16(1)(2)17.(!)(2)(3)18(!)(2)19.(1)(2)20.(1)(2)高三年级八校联考理科数学答案(2016.4)一.选择题题号12345678答案CCBBDAAD二.填空题9[1,3)10.11.12.13.14.三.解答题15(I)因此的最小正周期为,最大值为(II)当时,,从而当时,即时,单调递增.当时,即时,单调递减.综上可知,在上单调递增;在上单调递减.16(1)由题意,参加集训的男、女生各有6名.参赛学生全从B中学抽取的概率为.因此,A中学至少有1名学生入选代表队的概率为.(2)根据题意,的可能取值为1,2,3.所以的分布列为123因此,的数学期望为.17.解:(1)证明:因为,所以因为平面平面,平面平面,平,所以平面。(2)如图,取的中点,连接,因为,所以,因为平面平面,所以平面。以为原点,所在直线为轴,在平面内过垂直于的直线为轴,所在直线为轴建立空间直角坐标系。不妨设。由得,。所以,设平面的法向量为.因为,所以令,则。所以。取平面的一个法向量,所以所以平面与平面所成的锐二面角的大小为(3)在棱PB上存在点M使得CM∥平面PAD,此时。取AB的中点N,连接CM,CN,MN,则MN∥PA,AN=AB。因为AB=2CD,所以A...