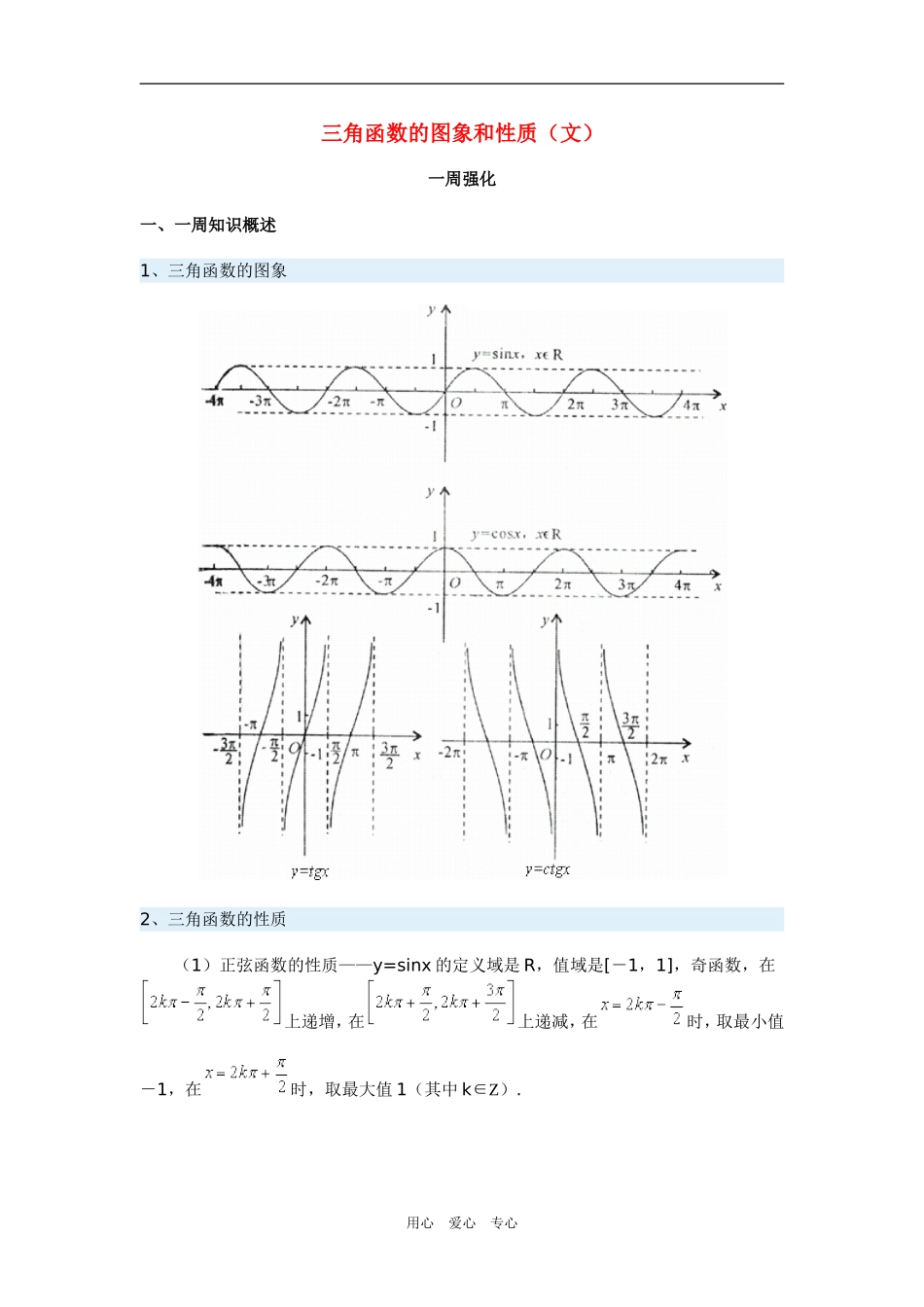
三角函数的图象和性质(文)一周强化一、一周知识概述1、三角函数的图象2、三角函数的性质(1)正弦函数的性质——y=sinx的定义域是R,值域是[-1,1],奇函数,在上递增,在上递减,在时,取最小值-1,在时,取最大值1(其中k∈Z).用心爱心专心(2)余弦函数的性质——y=cosx的定义域是R,值域是[-1,1],偶函数,在[2kπ,2kπ+π]上递减,在[2kπ+π,2kπ+2π]上递增,在x=2kπ时取最大值1,在x=2kπ+π时取最小值-1(其中K∈Z).(3)正切函数的性质——y=tgx的定义域是,值域是R,奇函数,在上递增,没有最大、最小值(其中k∈Z).(4)三角函数的周期①周期函数——对于函数y=f(x),如果存在一个不为零的常数T,使得当x取定义域内的每一个值时,f(x+T)=f(x)都成立,那么就把函数y=f(x)叫做周期函数,不为零的常数T叫做这个函数的周期.②最小正周期——对于一个周期函数来说,如果在所有的周期中存在着一个最小的正数,就把这个最小的正数叫做最小的正周期.③三角函数的最小正周期——y=sinx和y=cosx的最小正周期T=2π,y=tgx和y=ctgx的最小正周期T=π.3、函数y=sinx与y=Asin(ωx+Φ),(A>0,Φ>0)的比较.函数y=sinxy=Asin(ωx+Φ)区别奇偶性奇当,k∈Z时,非奇非偶周期性T=2π单调性,k∈Z用心爱心专心,k∈Z极值对称性对称轴:对称中心:(kπ,0),k∈Z对称轴:对称中心:联系y=Asin(ωx+Φ)的图像可以看作:把y=sinx的图像上所有的点向左(Φ>0)或向右(Φ<0)平移|Φ|个单位,再把所得点的横坐标缩短(ω>1)或伸长(0<ω<1)到原来的倍(纵坐标不变),再把所得各点的纵坐标伸长(A>1)或缩短(0<A<1)到原来的A倍(横坐标不变)而得到.二、重、难点知识的归纳与剖析1、本周学习的重点(1)三角函数不等式的解法与三角函数单调区间的求法.(2)三角函数的最值问题.(3)三角函数的图象与性质的运用.(4)周期性、对称性在解题中的应用.2、本周学习的难点(1)正确、有效地运用三角函数的图象解决问题.(2)已知三角函数值求角.(3)对符号“arcsina”、“arccosa”、“arctana”的正确理解,及正确运用这三个符号表示角.用心爱心专心(4)三角函数的图象变换.三、例题点评例1、用五点法作出函数的图象,并说明它与y=sinx的图像间的变换关系.例2、(1)求函数的定义域、值域;(2)求函数的值域.例3、求下列函数的单调递减区间.用心爱心专心例4、已知函数f(x)=1-2a-2acosx-2sin2x的最小值为g(a),a∈R.(1)求g(a);(2)若,求a及此时f(x)的最大值.例5、已知y=f(x)是定义在R上的函数,且对任意x∈R,有f(x+2)[1-f(x)]=f(x)+1成立.(1)证明y=f(x)是周期函数;(2)若f(1)=-2,求f(2005)的值.试题答案例1:解析:周期,振幅A=2,选取五点列表:x0π2πy020-20描点作图:用心爱心专心函数的图象可以看作是由下面的方法得到:先把y=sinx的图像上的所有的点向左平行移动个单位,得到的图像;再把的图像上所有的点的横坐标伸长到原来的2倍(纵坐标不变),得到的图像;再把的图像上所有的点的纵坐标伸长到原来的2倍(横坐标不变),从而得到的图像.例2:解析:(1)由≥0,得sinx≤,通过作单位圆,知定义域为用心爱心专心即.当;当,所以函数的值域为评析:解最简单的三角不等式时应用单位圆或函数的图像.(2)解法一:设sinx=t,则,由|sinx|≤1,得≤1,解这个不等式,得y≥2或y≤解法二:,∴|sinx|≤1,且sinx≠-∴-<sinx≤1时,0<3sinx+2≤5,∴,即y≤.用心爱心专心当-1≤sinx<-时,-1≤3sinx+2<0,∴≤-1,即y≥2.评析:关于三角函数,除符合代数函数的所有关系和性质外,还要注意它自己的属性.例3:分析:求三角函数的单调区间,利用三角函数的图象,可以化抽象为直观.解答:故原函数的单调递减区间为.(2)要求的单调递减区间,即求(u>0)的单调递增区间.用心爱心专心故原函数的单调递减区间为.点评:求三角函数的单调区间,一般先利用诱导公式将x的系数和三角函数符号前的系数都化为正值,再利用三角函数的图象求单调区间.例4:解析:(1)若,即a<-2时,则当cosx=-1时有最小值,;若-1≤≤1,即-2≤a≤2时,...