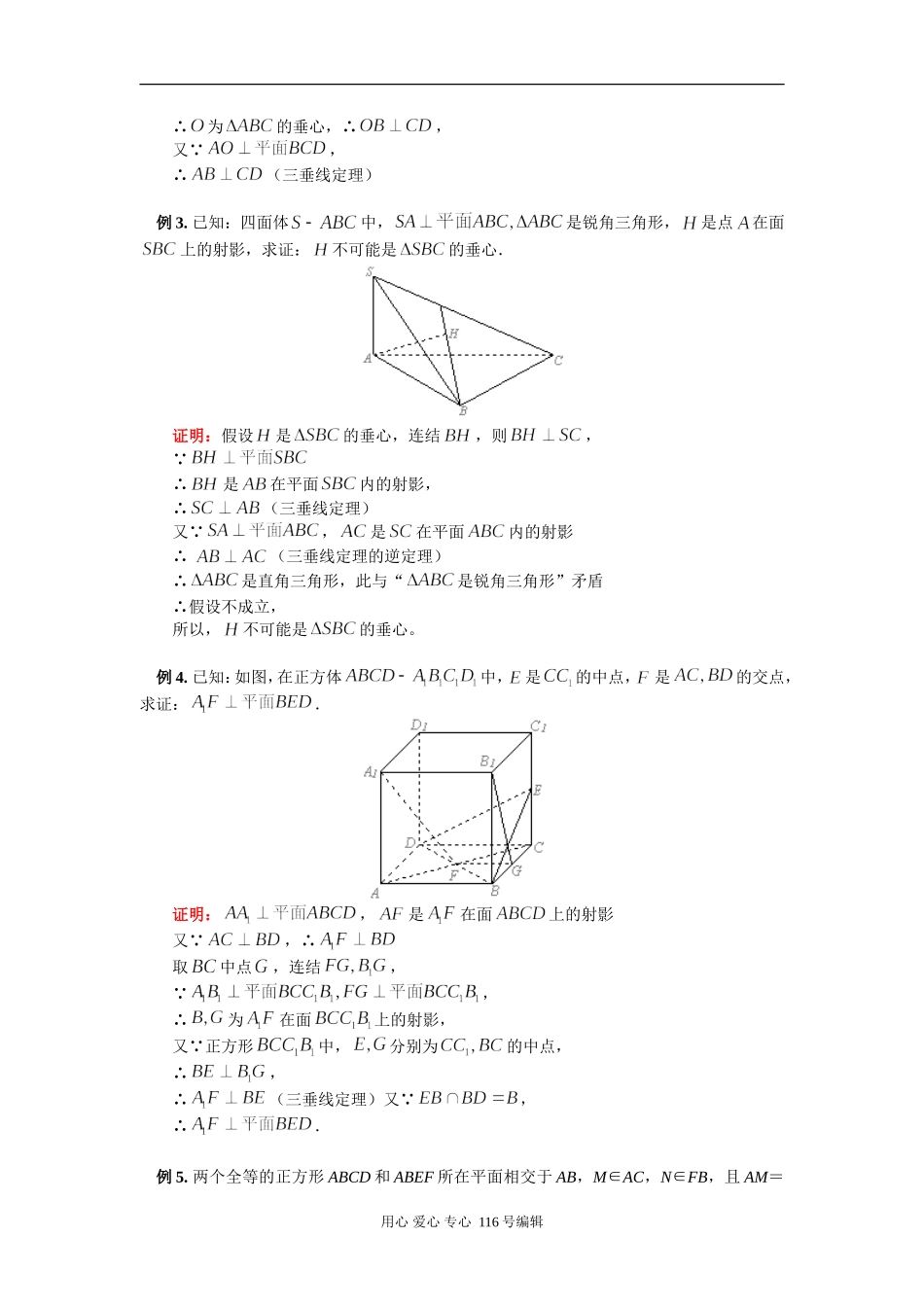
高三数学立体几何中的垂直问题知识精讲苏教版【本讲教育信息】一.教学内容:立体几何中的垂直问题二.高考要求:1.理解直线和平面垂直的概念新疆源头学子小屋特级教师王新敞http://www.xjktyg.com/wxc/wxckt@126.comwxckt@126.comhttp://www.xjktyg.com/wxc/王新敞特级教师源头学子小屋新疆掌握直线和平面垂直的判定定理;2.掌握直线和平面垂直的判定定理和性质定理。3.通过例题的讲解给学生总结归纳证明线面垂直的常见方法:(1)证直线与平面内的两条相交直线都垂直;(2)证与该线平行的直线与已知平面垂直;(3)借用面面垂直的性质定理;(4)同一法;(5)向量法。三.知识点归纳:1.线面垂直定义:如果一条直线和一个平面相交,并且和这个平面内的任意一条直线都垂直,我们就说这条直线和这个平面互相垂直。其中直线叫做平面的垂线,平面叫做直线的垂面奎屯王新敞新疆交点叫做垂足。直线与平面垂直简称线面垂直,记作:a⊥α。2.直线与平面垂直的判定定理:如果一条直线和一个平面内的两条相交直线都垂直,那么这条直线垂直于这个平面。3.直线和平面垂直的性质定理:如果两条直线同垂直于一个平面,那么这两条直线平行。4.三垂线定理在平面内的一条直线,如果它和这个平面的一条斜线的射影垂直,那么它也和这条斜线垂直。说明:(1)定理的实质是判定平面内的一条直线和平面的一条斜线的垂直关系;(2)推理模式:。5.三垂线定理的逆定理:在平面内的一条直线,如果和这个平面的一条斜线垂直,那么它也和这条斜线的射影垂直。推理模式:注意:⑴三垂线指PA,PO,AO都垂直α内的直线a。其实质是:斜线和平面内一条直线垂直的判定和性质定理。⑵要考虑a的位置,并注意两定理交替使用。6.两个平面垂直的定义:两个相交成直二面角的两个平面互相垂直;相交成直二面角的两个平面叫做互相垂直的平面。7.两平面垂直的判定定理:如果一个平面经过另一个平面的一条垂线,那么这两个平面互相垂直。推理模式:,.8.两平面垂直的性质定理:若两个平面互相垂直,那么在一个平面内垂直于它们的交线的直线垂直于另一个平面。用心爱心专心116号编辑推理模式:。9.向量法证明直线与平面、平面与平面垂直的方法:10.垂直和平行涉及题目的解决方法须熟练掌握两类相互转化关系:(1)平行转化:线线平行线面平行面面平行。(2)垂直转化:线线垂直线面垂直面面垂直。每一垂直或平行的判定就是从某一垂直或平行开始转向另一垂直或平行,最终达到目的。【典型例题】例1.如图,道路两旁有一条河,河对岸有电塔,高,只有量角器和皮尺作测量工具,能否测出电塔顶与道路的距离?解:在道路边取点,使与道路边所成的水平角等于,再在道路边取一点,使水平角,测得的距离等于, 是在平面上的射影,且∴(三垂线定理)因此斜线段的长度就是塔顶与道路的距离, ,∴,在中得,答:电塔顶与道路距离是.例2.点为所在平面外的一点,点为点在平面内的射影,若,求证:.证明:连结, ,且∴(三垂线定理的逆定理)同理,用心爱心专心116号编辑∴为的垂心,∴,又 ,∴(三垂线定理)例3.已知:四面体中,是锐角三角形,是点在面上的射影,求证:不可能是的垂心.证明:假设是的垂心,连结,则, ∴是在平面内的射影,∴(三垂线定理)又 ,是在平面内的射影∴(三垂线定理的逆定理)∴是直角三角形,此与“是锐角三角形”矛盾∴假设不成立,所以,不可能是的垂心。例4.已知:如图,在正方体中,是的中点,是的交点,求证:.证明:,是在面上的射影又 ,∴取中点,连结, ,∴为在面上的射影,又 正方形中,分别为的中点,∴,∴(三垂线定理)又 ,∴.例5.两个全等的正方形ABCD和ABEF所在平面相交于AB,M∈AC,N∈FB,且AM=用心爱心专心116号编辑FN,求证:MN∥平面BCE。命题意图:本题主要考查线面平行的判定,面面平行的判定与性质,以及一些平面几何的知识。知识依托:解决本题的关键在于找出面内的一条直线和该平面外的一条直线平行,即线(内)∥线(外)线(外)∥面。或转化为证两个平面平行。错解分析:证法二中要证线面平行,通过转化证两个平面平行,正确的找出MN所在平面是一个关键。...