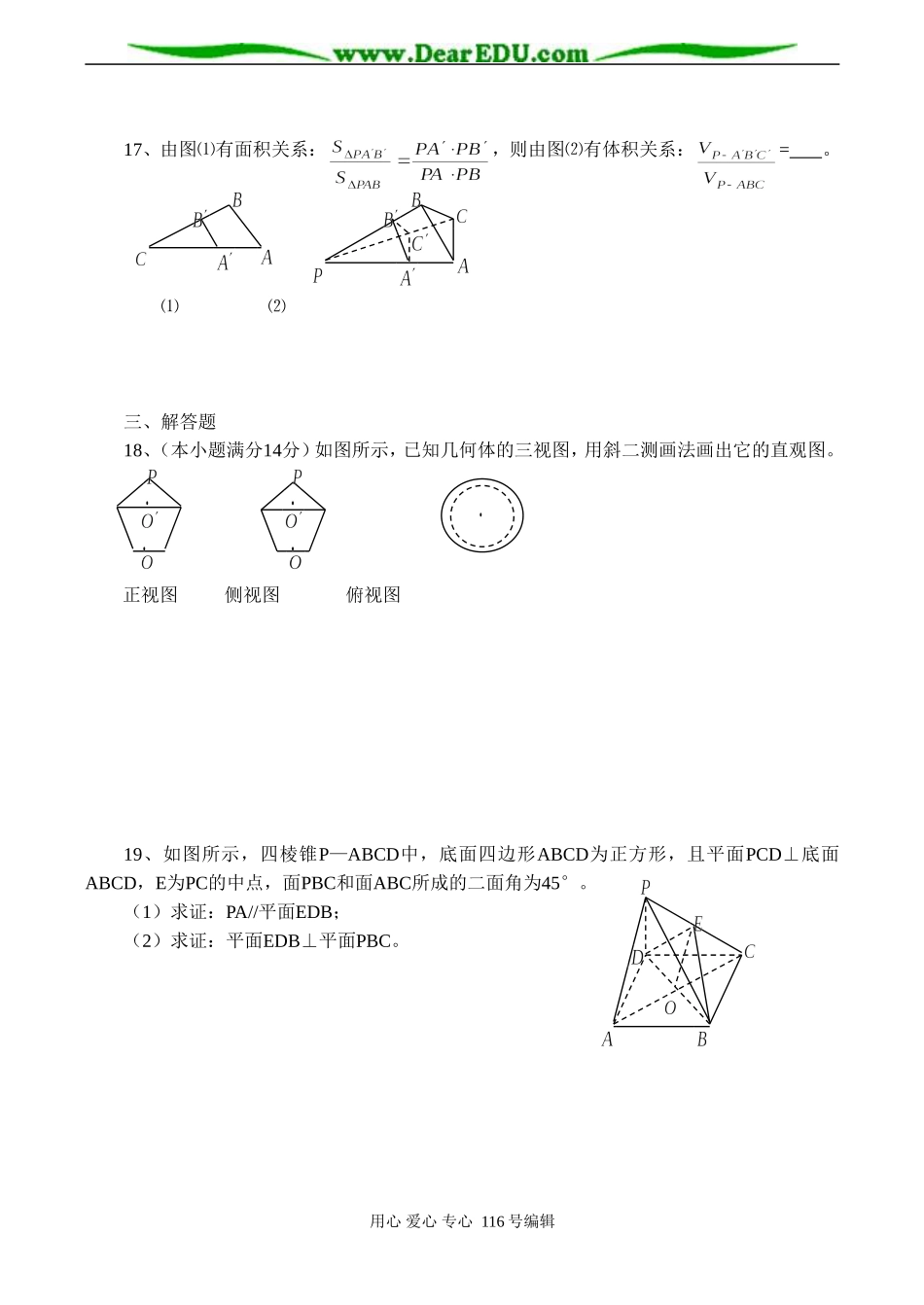
高一数学立体几何初步章节测试题一、选择题(每小题5分,共60分)1、已知是直线,α,β,γ是平面,给出下列命题:①,则α⊥β;②则α//β;③,则;④,则,其中正确的命题序号是()A、①④B、①③C、①②④D、③④2、一个长方体共一顶点的三个面的面积分别是,则这个长方体的对角线的长为()A、B、C、6D、3、相交成60°角的两条直线与平面α所成的角是45°,则这两条直线在平面α内射影的夹角是()A、90°B、60°C、45°D、30°4、已知棱锥的顶点为P,P在底面上的射影为O,PO=,现用平行于底面的平面去截这个棱锥,截面交PO于M,并使截得的两部分侧面积相等,设OM=,则的关系是()A、B、C、D、5、一个与球心距离为1的平面截球所得的圆面积为π,则球的表面积为()A、B、8πC、D、4π6、设三棱柱ABC—A1B1C1的体积为V,P、Q分别是侧棱AA1,CC1上的点,且PA=QC1,则四棱锥B—APQC的体积为()A、B、C、D、7、如图,四棱锥S—ABCD的底面是边长为1的正方形,SD⊥底面ABCD,SB=,则平面ASD与平面BSC所成的二面角大小为()A、30°B、45°C、60°D、90°8、下列图形中,不是三棱柱的展开图的是()ABCD9、如图所示的直观图,其平面图形的面积为()A、3B、用心爱心专心116号编辑C、6D、10、如图所示,在正方体ABCD—A1B1C1D1的侧面AB1内有一动点P到直线A1B1与直线BC的距离相等,则动点P所在曲线的形状为图中的()ABCD11、四面体PABC中,PA、PB、PC两两垂直,则P在平面ABC的正投影是△ABC的()A、内心B、外心C、重心D、垂心12、△ABC的边AB=5,BC=3,AC=4,设分别以此三边为轴,把△ABC旋转一周,所得旋转体的体积为VAB,VBC,VAC,则它们的大小关系是()A、VAB>VAC>VBCB、VAB>VBC>VACC、VAB>VBC>VACD、VBC>VAC>VAB二、填空(每小题5分,共20分)13、已知正四棱锥P—ABCD的五个顶点都在同一球面上,若该正四棱锥的底面边长为4,侧棱长为,则此球的表面积为。14、在正方体ABCD—A1B1C1D1中,过对角线BD1的一个平面交AA1于E,交CC1于F,则:①四边形BFD1E一定是平行四边形;②四边形BFD1E有可能是正方形;③四边形BFD1E在底面ABCD内的投影一定是正方形;④平面BFD1E有可能垂直于平面BB1D。以上结论正确的为。(写出所有正确结论的编号)15、如图所示,E、F分别是正方体的面ADD1A1、面BCC1B1的中心,则四边形BFD1E在该正方体的面上的射影可能是图中的(要求:把可能的图的序号都填上)。①②③④16、α、β是两个不同的平面,m、n是平面α及β之外的两条不同直线,给出四个论断:①m⊥n,②α⊥β,③n⊥β,④m⊥α,以其中三个论断为条件,余下的一个作为结论,写出一个正确的命题。用心爱心专心116号编辑BCAD17、由图⑴有面积关系:,则由图⑵有体积关系:=。⑴⑵三、解答题18、(本小题满分14分)如图所示,已知几何体的三视图,用斜二测画法画出它的直观图。正视图侧视图俯视图19、如图所示,四棱锥P—ABCD中,底面四边形ABCD为正方形,且平面PCD⊥底面ABCD,E为PC的中点,面PBC和面ABC所成的二面角为45°。(1)求证:PA//平面EDB;(2)求证:平面EDB⊥平面PBC。用心爱心专心116号编辑20、(本小题满分14分)如图所示,把边长为的正方形剪去图中阴影部分,沿图中的线折成一个正三棱锥,求出此棱锥的底面积,侧面积和高。21、(本小题满分14分)如图所示,已知BB1CC1是Rt△ABC所在平面同侧的两条相等的斜线段,它们与平面ABC所成的角均为60°,且BB1//CC1,线段BB1的端点B1在平面ABC上的射影M恰是BC的中点,已知BC=2cm,∠ACB=90°。⑴求异面直线AB1与BC1所成的角;⑵若二面角A—B1B—C为30°,求三棱锥C1—ABC的体积;(3)求直线AB1与平面BCC1B1所成的角。22、(本小题满分14分)已知AB是球O的直径,C、D是球面上的两点,且D在以BC为直径的小圆上,设此小圆所在平面为α,(1)求证:平面ACB⊥α;(2)设AB与α所成角为θ,过球半径OD且垂直于α的截面截BC弦于E点,求△OED与经过点O、D的截面面积之比,并求θ为何值时,它们的面积之比最大。用心爱心专心116号编辑用心爱心专心116号编辑