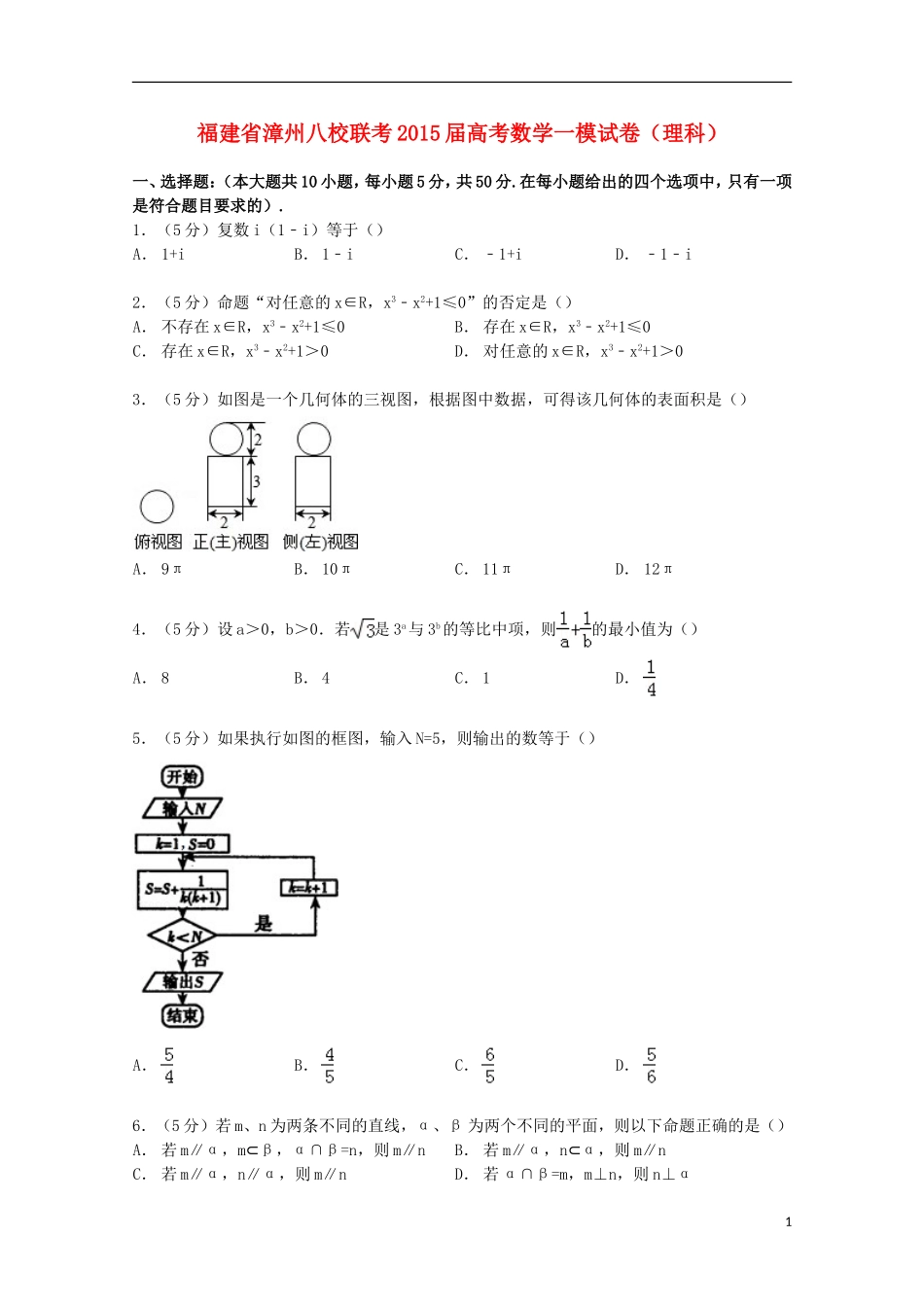
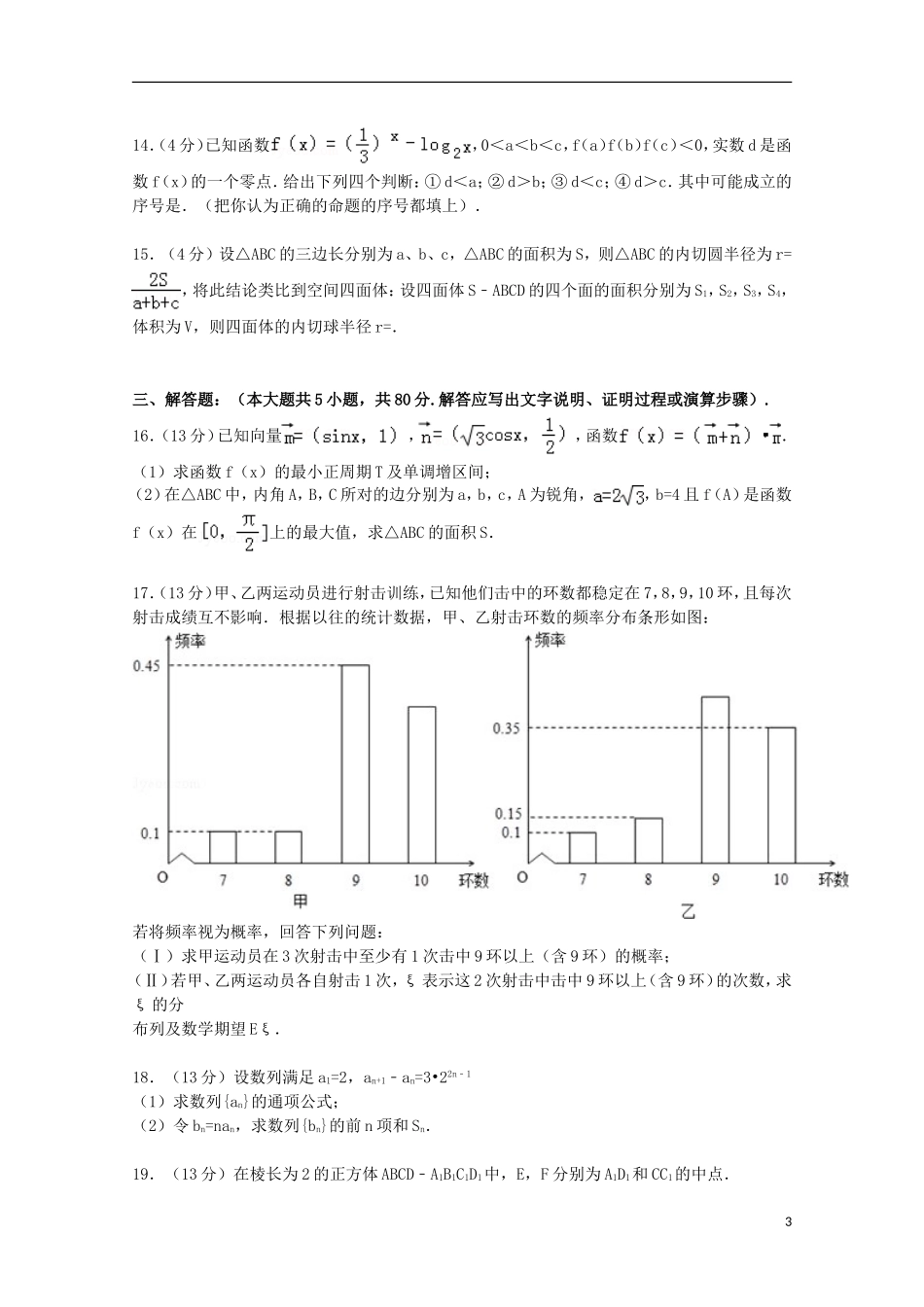
福建省漳州八校联考2015届高考数学一模试卷(理科)一、选择题:(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的).1.(5分)复数i(1﹣i)等于()A.1+iB.1﹣iC.﹣1+iD.﹣1﹣i2.(5分)命题“对任意的x∈R,x3﹣x2+1≤0”的否定是()A.不存在x∈R,x3﹣x2+1≤0B.存在x∈R,x3﹣x2+1≤0C.存在x∈R,x3﹣x2+1>0D.对任意的x∈R,x3﹣x2+1>03.(5分)如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是()A.9πB.10πC.11πD.12π4.(5分)设a>0,b>0.若是3a与3b的等比中项,则的最小值为()A.8B.4C.1D.5.(5分)如果执行如图的框图,输入N=5,则输出的数等于()A.B.C.D.6.(5分)若m、n为两条不同的直线,α、β为两个不同的平面,则以下命题正确的是()A.若m∥α,m⊂β,α∩β=n,则m∥nB.若m∥α,n⊂α,则m∥nC.若m∥α,n∥α,则m∥nD.若α∩β=m,m⊥n,则n⊥α17.(5分)如图所示,在边长为1的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为()A.B.C.D.8.(5分)为得到函数的图象,只需将函数y=sin2x的图象()A.向左平移个长度单位B.向右平移个长度单位C.向左平移个长度单位D.向右平移个长度单位9.(5分)设变量x,y满足约束条件:.则目标函数z=2x+3y的最小值为()A.6B.7C.8D.2310.(5分)设非空集合S={x|m≤x≤n}满足:当x∈S时,有x2∈S.给出如下三个命题:①若m=1,则S={1};②若m=﹣,则≤n≤1;③若n=,则﹣≤m≤0.其中正确命题的个数是()A.0B.1C.2D.3二、填空题:(本大题共5小题,每小题4分,共20分.把答案填在答题卷中的横线上).11.(4分)设向量,且∥,则cos2θ=.12.(4分)的展开式的常数项是(用数字作答)13.(4分)如图,一矩形铁皮的长为8cm,宽为5cm,在四个角上截去四个相同的小正方形,制成一个无盖的小盒子,则小正方形的边长为时,盒子容积最大?214.(4分)已知函数,0<a<b<c,f(a)f(b)f(c)<0,实数d是函数f(x)的一个零点.给出下列四个判断:①d<a;②d>b;③d<c;④d>c.其中可能成立的序号是.(把你认为正确的命题的序号都填上).15.(4分)设△ABC的三边长分别为a、b、c,△ABC的面积为S,则△ABC的内切圆半径为r=,将此结论类比到空间四面体:设四面体S﹣ABCD的四个面的面积分别为S1,S2,S3,S4,体积为V,则四面体的内切球半径r=.三、解答题:(本大题共5小题,共80分.解答应写出文字说明、证明过程或演算步骤).16.(13分)已知向量,,函数.(1)求函数f(x)的最小正周期T及单调增区间;(2)在△ABC中,内角A,B,C所对的边分别为a,b,c,A为锐角,,b=4且f(A)是函数f(x)在上的最大值,求△ABC的面积S.17.(13分)甲、乙两运动员进行射击训练,已知他们击中的环数都稳定在7,8,9,10环,且每次射击成绩互不影响.根据以往的统计数据,甲、乙射击环数的频率分布条形如图:若将频率视为概率,回答下列问题:(Ⅰ)求甲运动员在3次射击中至少有1次击中9环以上(含9环)的概率;(Ⅱ)若甲、乙两运动员各自射击1次,ξ表示这2次射击中击中9环以上(含9环)的次数,求ξ的分布列及数学期望Eξ.18.(13分)设数列满足a1=2,an+1﹣an=3•22n﹣1(1)求数列{an}的通项公式;(2)令bn=nan,求数列{bn}的前n项和Sn.19.(13分)在棱长为2的正方体ABCD﹣A1B1C1D1中,E,F分别为A1D1和CC1的中点.3(Ⅰ)求证:EF∥平面ACD1;(Ⅱ)求异面直线EF与AB所成的角的余弦值;(Ⅲ)在棱BB1上是否存在一点P,使得二面角P﹣AC﹣B的大小为30°?若存在,求出BP的长;若不存在,请说明理由.20.(14分)已知函数f(x)=ln(x+1)+(a∈R)(Ⅰ)当a=2时,求函数y=f(x)的图象在x=0处的切线方程;(Ⅱ)判断函数f(x)的单调性;(Ⅲ)求证:ln(1+)﹣(n∈N*)四.本题有21、22、23三个选答题,每题7分,请考生任选2题作答,满分7分.如果多做,则按所做的前两题记分.【选修4-2:矩阵与变换】21.(7分)(矩阵与变换)已知矩阵,矩阵MN对应的变换把曲线y=sinx变为曲线C,求...