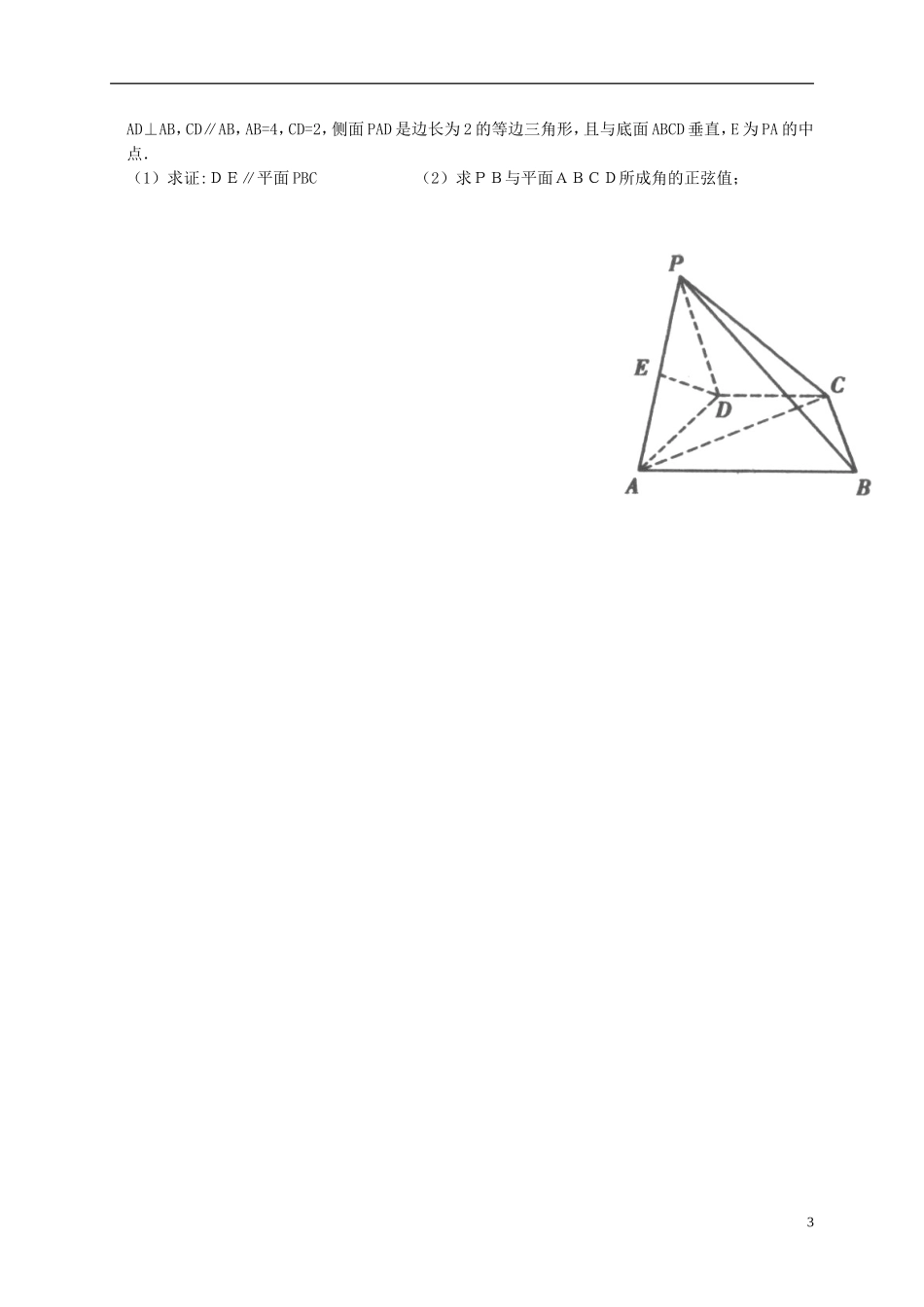
福建省泉州市泉港区2016-2017学年高一数学下学期期中试题(考试时间:120分钟总分:150分)★友情提示:要把所有答案都写在答题卷上,写在试卷上的答案无效。一、选择题(每题5分,共60分,在每小题给出的四个选项中只有一项是符合题目要求的)1.在空间直角坐标系中,A(0,2,4),B(1,4,6),则|AB|等于()A.2B.2C.D.32.直线l过点P(-1,2),倾斜角为135°,则直线l的方程为()A.x+y-1=0B.x-y+1=0C.x+y-3=0D.x-y+3=03.下列命题正确的是()A.若两个平面平行于同一条直线,则这两个平面平行B.若有两条直线与两个平面都平行,则这两个平面平行C.若有一条直线与两个平面都垂直,则这两个平面平行D.若有一条直线与这两个平面所成的角相等,则这两个平面平行4.已知水平放置的△ABC是按“斜二测画法”得到如图所示的直观图,其中B′O′=C′O′=1,A′O′=,那么原△ABC是一个()A.等边三角形B.直角三角形C.三边中只有两边相等的等腰三角形D.三边互不相等的三角形5.若某几何体的三视图(单位:cm)如图所示,则此几何体的侧面积等于()A.12πcm2B.15πcm2C.24πcm2D.30πcm26.若三棱锥P-ABC的三个侧面与底面ABC所成角都相等,则顶点P在底面的射影为的()A.外心B.重心C.内心D.垂心7.圆:与圆:的位置关系为()A.相交B.相离C.外切D.内切8.若P(2,-1)为圆的弦AB的中点,则直线AB的方程是()A.x-y-3=0B.2x+y-3=0C.x+y-1=0D.2x-y-5=09.已知点P是圆x2+y2=1上动点,定点Q(6,0),点M是线段PQ靠近Q点的三等分点,则点M的轨迹方程是()A.(x+3)2+y2=4B.(x-4)2+y2=C.(2x-3)2+4y2=1D.(2x+3)2+4y2=110.若圆上恰有四个点到直线的距离等于1,则实数m的取值范围是方程是()A.B.1C.D.11.已知实数x,y满足方程2x+y+5=0,那么的最小值为()A.2B.C.2D.12.函数的值域为()A.B.C.D.二、填空题(每小题5分,共20分)13.如图,在正方体中,分别为,,,的中点,则异面直线与所成的角等于14.已知直线和直线关于点M(2,1)对称,则的方程为15.如果直线与直线关于直线对称,那么16.已知⊙M:Q是轴上的动点,QA,QB分别切⊙M于A,B两点,求动弦AB的中点P的轨迹方程为三、解答题。(本大题共6小题,满分70分,解答应写出文字说明,推理过程或演算步骤)17.(本小题满分10分)求经过直线:与直线:的交点,且满足下列条件的直线的方程:(1)与直线平行;(2)与直线垂直。18.(本小题满分12分)如图,在四棱锥P-ABCD中,底面是直角梯形ABCD,其中2AFDBCGE1BH1C1D1AAD⊥AB,CD∥AB,AB=4,CD=2,侧面PAD是边长为2的等边三角形,且与底面ABCD垂直,E为PA的中点.(1)求证:DE∥平面PBC(2)求PB与平面ABCD所成角的正弦值;319.(本小题满分12分)已知ABC的顶点A(2,3),B(-2,1),重心G(1,2)(1)求BC边中点D的坐标;(2)求AB边的高线所在直线的方程;(3)求ABC的面积;20.(本小题满分12分)已知圆C:(x-2)2+(y-3)2=16及直线l:(m+2)x+(3m+1)y=15m+10(m∈R).(1)证明:不论m取什么实数,直线l与圆C恒相交;(2)当直线l被圆C截得的弦长的最短时,求此时直线l方程.21、(本小题满分12分)如图,已知四边形是正方形,平面ABCD,//,,,,分别为,,的中点.(1)求四棱锥P—BCD外接球(即P,B,C,D四点都在球面上)的表面积;(2)求证:平面平面;(3)在线段上是否存在一点,使平面?若存在,求出线段的长;若不存在,请说明理由.422、(本小题满分12分)如图,已知圆C:x2+y2-4x-14y+45=0及点Q(-2,3)(1)若点P(m,m+1)在圆C上,求直线PQ的斜率以及直线PQ与圆C的相交弦PE的长度;(2)若N(x,y)是直线上任意一点,过N作圆C的切线,切点为A,当切线长最小时,求N点的坐标,并求出这个最小值.(3)若M(x,y)是圆上任意一点,求的最大值和最小值.高一数学科试题参考答案一、选择题1—5:DACAB6—10:CCABB11—12:CD二、13.60°14.15.16.三、解答题17:解:(1)交点M(-3,-2.5)…………3分…………6分(2)…………10分18.如图,在四棱锥P-ABCD中,底面是直角梯形ABCD,其中AD⊥AB,CD∥AB,AB=4,CD=2,侧面PAD是5边长为2的等边...