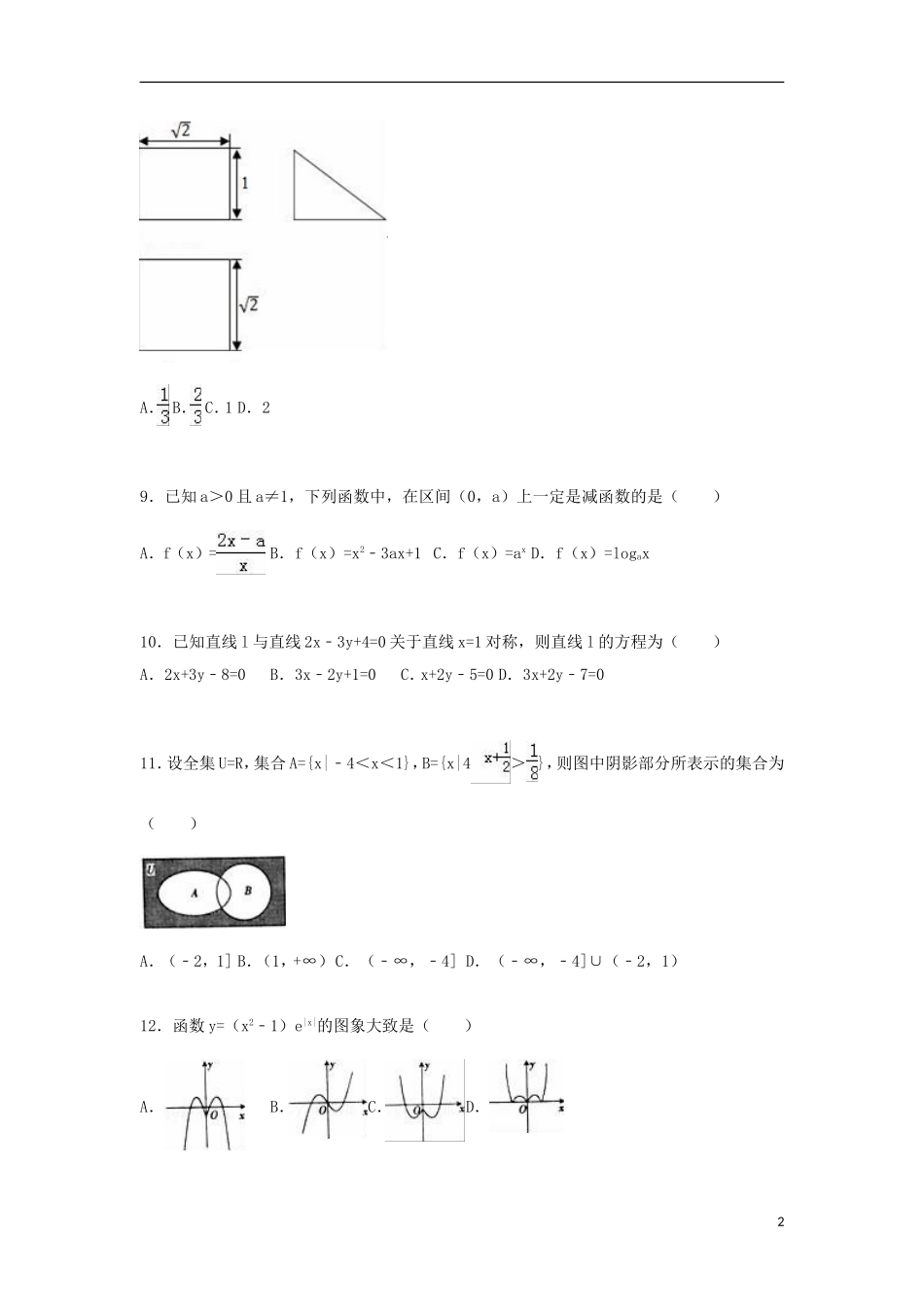
2015-2016学年福建省南平市高一(上)期末数学试卷一、选择题(共12小题,每小题5分,满分60分)1.已知直线x﹣ay=4在y轴上的截距是2,则a等于()A.﹣B.C.﹣2D.22.已知集合A={1,2,3,4,5},B={x|x<2},则A∩B等于()A.{1}B.{1,2}C.{1,2,3}D.{1,2,3,4}3.函数f(x)=3x+x﹣5,则函数f(x)的零点一定在区间()A.(0,1)B.(1,2)C.(2,3)D.(3,4)4.以(﹣2,1)为圆心且与直线x+y=3相切的圆的方程为()A.(x﹣2)2+(y+1)2=2B.(x+2)2+(y﹣1)2=4C.(x﹣2)2+(y+1)2=8D.(x+2)2+(y﹣1)2=85.已知直线l⊥平面α,直线m⊂平面β,下列命题正确的是()A.若α⊥β,则l∥mB.若l⊥m,则α∥βC.若l∥β,则m⊥αD.若α∥β,则l⊥m6.已知a=ln,b=5lg3,c=3,则a,b,c的大小关系为()A.a<b<cB.a<c<bC.b<a<cD.b<c<a7.两平行线3x﹣4y﹣2=0与3x﹣4y+8=0之间的距离为()A.2B.C.1D.28.若某空间几何体的三视图如图所示,则该几何体的体积是()1A.B.C.1D.29.已知a>0且a≠1,下列函数中,在区间(0,a)上一定是减函数的是()A.f(x)=B.f(x)=x2﹣3ax+1C.f(x)=axD.f(x)=logax10.已知直线l与直线2x﹣3y+4=0关于直线x=1对称,则直线l的方程为()A.2x+3y﹣8=0B.3x﹣2y+1=0C.x+2y﹣5=0D.3x+2y﹣7=011.设全集U=R,集合A={x|﹣4<x<1},B={x|4>},则图中阴影部分所表示的集合为()A.(﹣2,1]B.(1,+∞)C.(﹣∞,﹣4]D.(﹣∞,﹣4]∪(﹣2,1)12.函数y=(x2﹣1)e|x|的图象大致是()A.B.C.D.2二、填空题(共4小题,每小题5分,满分20分)13.已知点(1,﹣1,2)关于x轴对称点为A,则点A的坐标为.14.已知球O的表面积是其半径的6π倍,则该球的体积为.15.已知定义在(,+∞)的函数f(x)满足f(x+1)﹣f(x)=log3(x﹣),若f(1)=2,则f(2)=.16.已知圆C:x2+y2﹣4x+m=0与圆(x﹣3)2+(y+2)2=4外切,点P是圆C上一动点,则点P到直线mx﹣4y+4=0的距离的最大值为.三、解答题(共6小题,满分70分)17.已知集合A={x|1≤x<4},B={x|x﹣a<0}.(1)当a=3时,求A∩B,A∪B;(2)若A⊆B,求实数a的取值范围.18.已知直线l:x﹣2y﹣1=0,直线l1过点(﹣1,2).(1)若l1⊥l,求直线l1的方程;(2)若l1∥l,求直线l1的方程.19.已知函数f(x)满足f()=x+.(1)求函数的解析式;(2)判断函数f(x)在区间(,+∞)上的单调性,并用定义法加以证明.320.已知四棱锥P﹣ABCD的底面是菱形.PB=PD,E为PA的中点.(Ⅰ)求证:PC∥平面BDE;(Ⅱ)求证:平面PAC⊥平面BDE.21.已知函数f(x)=()x+a的图象经过第二、三、四象限.(1)求实数a的取值范围;(2)设g(a)=f(a)﹣f(a+1),求g(a)的取值范围.22.已知圆C关于直线x+y+2=0对称,且过点P(﹣2,2)和原点O.(1)求圆C的方程;(2)相互垂直的两条直线l1,l2都过点A(﹣1,0),若l1,l2被圆C所截得弦长相等,求此时直线l1的方程.42015-2016学年福建省南平市高一(上)期末数学试卷参考答案与试题解析一、选择题(共12小题,每小题5分,满分60分)1.已知直线x﹣ay=4在y轴上的截距是2,则a等于()A.﹣B.C.﹣2D.2【考点】直线的截距式方程.【专题】计算题;方程思想;综合法;直线与圆.【分析】直接把点(0,2)代入直线方程,求出a即可.【解答】解:已知直线x﹣ay=4在y轴上的截距是2,即直线过(0,2),代入得:﹣2a=4,则a=﹣2,故选:C.【点评】本题考查了一次函数图象上点的坐标的特点,是一道基础题.2.已知集合A={1,2,3,4,5},B={x|x<2},则A∩B等于()A.{1}B.{1,2}C.{1,2,3}D.{1,2,3,4}【考点】交集及其运算.【专题】计算题;集合思想;集合.【分析】由A与B,求出两集合的交集即可.【解答】解: A={1,2,3,4,5},B={x|x<2},∴A∩B={1},故选:A.【点评】此题考查了交集及其运算,熟练掌握交集的定义是解本题的关键.3.函数f(x)=3x+x﹣5,则函数f(x)的零点一定在区间()A.(0,1)B.(1,2)C.(2,3)D.(3,4)【考点】二分法求方程的近似解....