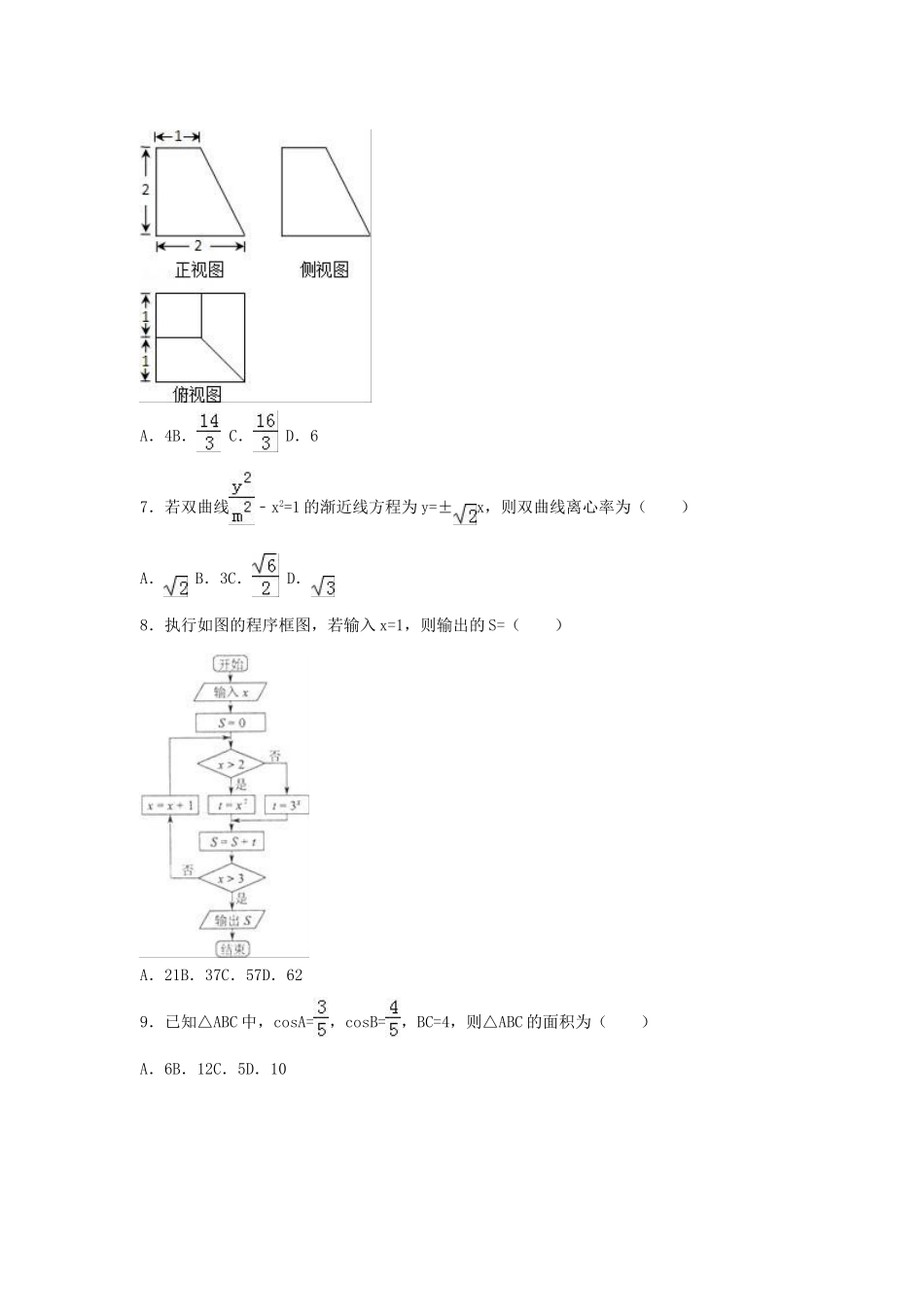
2016年甘肃省白银十中高考数学押题卷(理科)(二)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.如图所示的复平面上的点A,B分别对应复数z1,z2,则=()A.﹣2iB.2iC.2D.﹣22.已知集合A={x|x2﹣16<0},B={﹣5,0,1},则()A.A∩B=∅B.B⊆AC.A∩B={0,1}D.A⊆B3.已知{an}为正项等比数列,Sn是它的前n项和.若a1=16,且a4与a7的等差中项为,则S5的值()A.29B.31C.33D.354.在△ABC中,=,=,=,=,则=()A.+B.+C.+D.﹣5.数列{an}满足an+1=,若a1=,则a2015=()A.B.C.D.6.某四棱台的三视图如图所示,则该四棱台的体积是()A.4B.C.D.67.若双曲线﹣x2=1的渐近线方程为y=±x,则双曲线离心率为()A.B.3C.D.8.执行如图的程序框图,若输入x=1,则输出的S=()A.21B.37C.57D.629.已知△ABC中,cosA=,cosB=,BC=4,则△ABC的面积为()A.6B.12C.5D.1010.已知三角形PAD所在平面与矩形ABCD所在平面互相垂直,PA=PD=AB=2,∠APD=120°,若点P,A,B,C,D都在同一球面上,则此球的表面积等于()A.8πB.12πC.16πD.20π11.在1,2,3,4,5,6,7,8这组数据中,随机取出五个不同的数,则数字5是取出的五个不同数的中位数的概率为()A.B.C.D.12.已知椭圆具有如下性质:若椭圆的方程为=1(a>b>0),则椭圆在其上一点A(x0,y0)处的切线方程为=1,试运用该性质解决以下问题:椭圆C1:=1(a>b>0),其焦距为2,且过点.点B为C1在第一象限中的任意一点,过B作C1的切线l,l分别与x轴和y轴的正半轴交于C,D两点,则△OCD面积的最小值为()A.B.C.D.2二、填空题(本大题共4个小题,每小题5分,共20分,将正确答案填在题中横线上)13.数列{an}的通项公式an=,它的前n项和为Sn=9,则n=.14.某班有50名同学,一次数学考试的成绩X服从正态分布N,已知P=0.34,估计该班学生数学成绩在120分以上的有人.15.已知△ABC三个顶点的直角坐标分别为A(3,4)、B(0,0)、C(5,0).则sin∠A=.16.已知函数f(x)=|sinx|•cosx,给出下列五个结论:①f()=﹣;②若|f(x1)|=|f(x2)|,则x1=x2+kπ(k∈Z);③f(x)在区间[﹣,]上单调递增;④函数f(x)的周期为π;⑤f(x)的图象关于点(,0)成中心对称其中正确的结论是(写出所有正确结论的序号)三、解答题(解答应写出文字说明、证明过程或演算步骤)17.在△ABC中,a,b,c分别为内角A,B,C的对边,且b2+c2﹣a2=bc.(Ⅰ)求角A的大小;(Ⅱ)设函数,当f(B)取最大值时,判断△ABC的形状.18.如图,在三棱柱ABC﹣A1B1C1中,四边形AA1C1C是边长为4的正方形,平面ABC⊥平面AA1C1C,AB=3,BC=5(Ⅰ)求证:AA1⊥平面ABC;(Ⅱ)求二面角C﹣A1B1﹣C1的大小;(Ⅲ)若点D是线段BC的中点,请问在线段AB1上是否存在点E,使得DE∥面AA1C1C?若存在,请说明点E的位置;若不存在,请说明理由.19.今年柴静的《穹顶之下》发布后,各地口罩市场受其影响生意火爆.A市虽然雾霾现象不太严重,但经抽样有25%的市民表示会购买口罩.现将频率视为概率,解决下列问题:(1)从该市市民中随机抽取3位,求至少有一位市民会购买口罩的概率;(2)从该市市民中随机抽取4位,X表示愿意购买口罩的市民人数,求X的分布列及数学期望.20.已知椭圆C:+=1(a>b>0)过点A(﹣,),离心率为,点F1,F2分别为其左右焦点.(1)求椭圆C的标准方程;(2)若y2=4x上存在两个点M,N,椭圆上有两个点P,Q满足,M,N,F2三点共线,P,Q,F2三点共线,且PQ⊥MN.求四边形PMQN面积的最小值.21.函数f(x)=x2+mln(x+1).(1)若函数f(x)是定义域上的单调函数,求实数m的取值范围;(2)若m=﹣1,试比较当x∈(0,+∞)时,f(x)与x3的大小;(3)证明:对任意的正整数n,不等式e0+e﹣1×4+e﹣2×9+…+e<成立.请考生在第22、23、24题中任选一题作答,如果多做,则按所做的第一题计分.作答时请写清题号.[选修4-1几何证明选讲]22.如图,△ABC中,∠ACB=90°,D是AC上一点,以AD为直径作⊙O交AB于点G(1)证明:B、C、D、G四点...