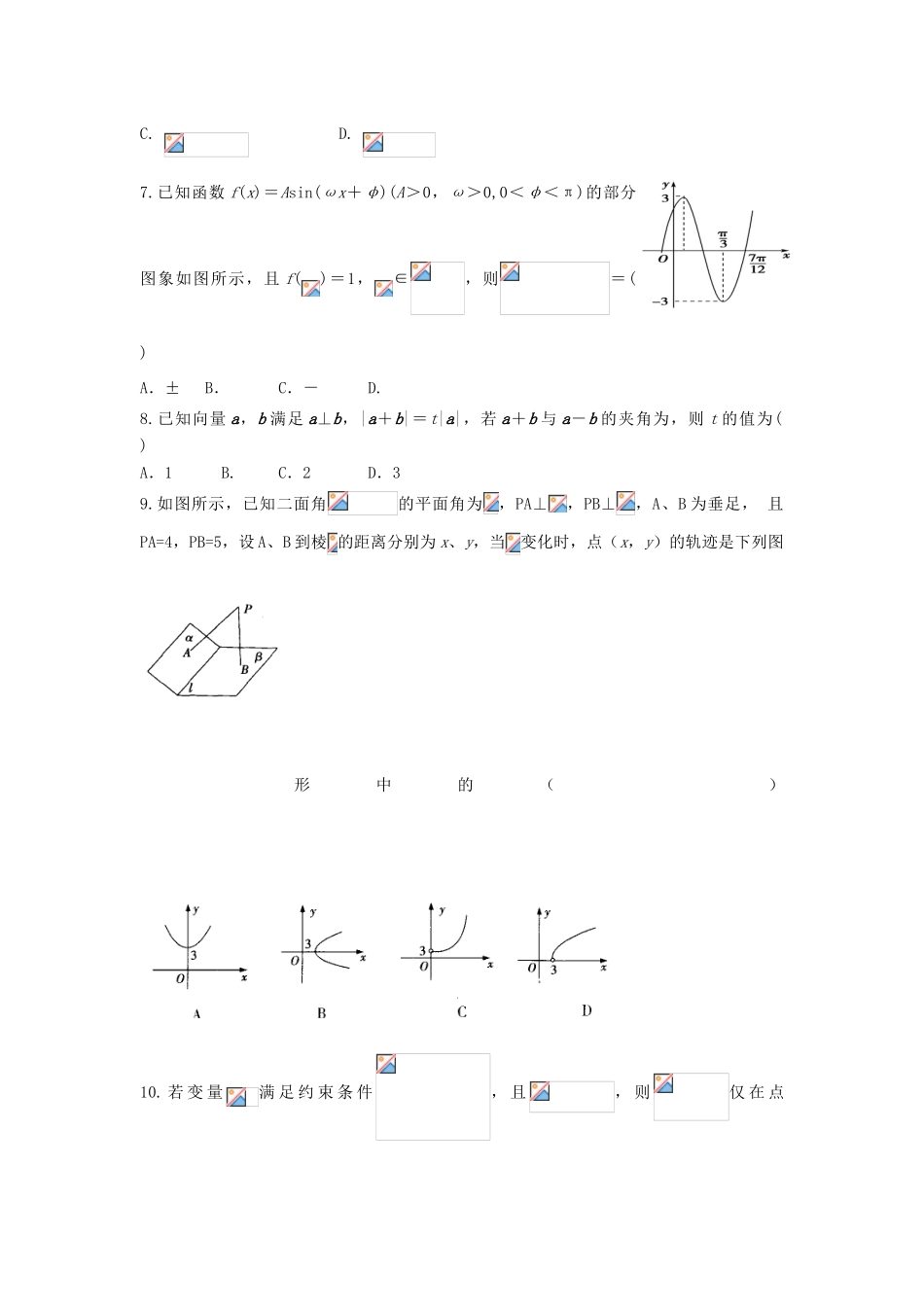
2017—2018学年第一学期高三年级十月份考试理科数学试卷本试卷分必考部分和选考两部分必考部分一、选择题(本题共12小题,每小题5分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.设集合,,则()A.B.C.D.2.已知(是虚数单位),那么复数z对应的点位于复平面内的()A.第一象限B.第二象限C.第三象限D.第四象限3.执行如图的程序框图,若输出的值为6,则判断框内可填入的条件是()A.B.C.D.4.已知等比数列,且,则的值为()A.B.C.D.5.一个几何体的三视图如图所示,其中正视图是一个正三角形,则这个几何体的外接球的表面积为()A.B.C.4πD.π6.已知函数满足,且的导函数,则的解集为()A.B.C.D.7.已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的部分图象如图所示,且f()=1,∈,则=()A.±B.C.-D.8.已知向量a,b满足a⊥b,|a+b|=t|a|,若a+b与a-b的夹角为,则t的值为()A.1B.C.2D.39.如图所示,已知二面角的平面角为,PA⊥,PB⊥,A、B为垂足,且PA=4,PB=5,设A、B到棱的距离分别为x、y,当变化时,点(x,y)的轨迹是下列图形中的()10.若变量满足约束条件,且,则仅在点处取得最大值的概率为()A.B.C.D.11.已知点A(-2,3)在抛物线C:y2=2px的准线上,过点A的直线与C在第一象限相切于点B,记C的焦点为F,则直线BF的斜率为()A.B.C.D.12.已知定义在上的函数满足①,②,③在[-1,1]上表达式为,则函数与函数的图象在区间[-3,3]上的交点个数为()A.5B.6C.7D.8二、填空题:本大题共4小题,每小题5分.13.等比数列的公比,已知,,则的前4项和_____14.设,若的最小值为15.若随机变量服从正态分布,,,设,且则16.已知数列的首项,其前项和为,且满足,若对,恒成立,则的取值范围是_______.三、解答题:解答应写出文字说明、证明过程或演算步骤.17.如图,某旅游区拟建一主题游乐园,该游乐区为五边形区域ABCDE,其中三角形区域ABE为主题游乐区,四边形区域为BCDE为休闲游乐区,AB、BC,CD,DE,EA,BE为游乐园的主要道路(不考虑宽度).(1)求道路BE的长度;(2)求道路AB,AE长度之和的最大值.18.一个不透明的袋子中装有4个形状相同的小球,分别标有不同的数字2,3,4,,现从袋中随机摸出2个球,并计算摸出的这2个球上的数字之和,记录后将小球放回袋中搅匀,进行重复试验。记A事件为“数字之和为7”.试验数据如下表:(Ⅰ)如果试验继续下去,根据上表数据,出现“数字之和为7”的频率将稳定在它的概率附近。试估计“出现数字之和为7”的概率,并求的值;(Ⅱ)在(Ⅰ)的条件下,设定一种游戏规则:每次摸2球,若数字和为7,则可获得奖金7元,否则需交5元。某人摸球3次,设其获利金额为随机变量元,求的数学期望和方差.19.如图,在四棱锥中,,平面,.(1)设点为的中点,求证:平面;(2)线段上是否存在一点,使得直线与平面所成的角的正弦值为?若存在,试确定点的位置;若不存在,请说明理由.20.如图,设椭圆的左、右焦点分别为,点在椭圆上,,,的面积为.(1)求该椭圆的标准方程;(2)是否存在圆心在轴上的圆,使圆在轴的上方与椭圆有两个交点,且圆在这两个交点处的两条切线相互垂直并分别过不同的焦点?若存在,求圆的方程,若不存在,请说明理由.21.若存在实常数和,使得函数和对其定义域上的任意实数分别满足:和,则称直线为和的“隔离直线”.已知,为自然对数的底数).(1)求的极值;(2)函数和是否存在隔离直线?若存在,求出此隔离直线方程;若不存在,请说明理由.选考部分请考生在22、23题中任选一题作答,如果多做,则按所做的第一题计分。22.选修4-4:坐标系与参数方程在直角坐标系中,已知圆:(为参数),点在直线:上,以坐标原点为极点,轴的正半轴为极轴,建立极坐标系.(1)求圆和直线的极坐标方程;(2)射线交圆于,点在射线上,且满足,求点轨迹的极坐标方程.23.选修4-5不等式选讲若函数的最小值为2.(1)求实数的值;(2)若,且,证明:.2017—2018学年第一学期高三年级十月份考试理科数学试卷答案题号123456789101112答案BCADADCCDCDD13.14.15.216.17.(Ⅰ)如图,连接,在中,由余弦定理得:,,,,又,,所以在中,;(Ⅱ...