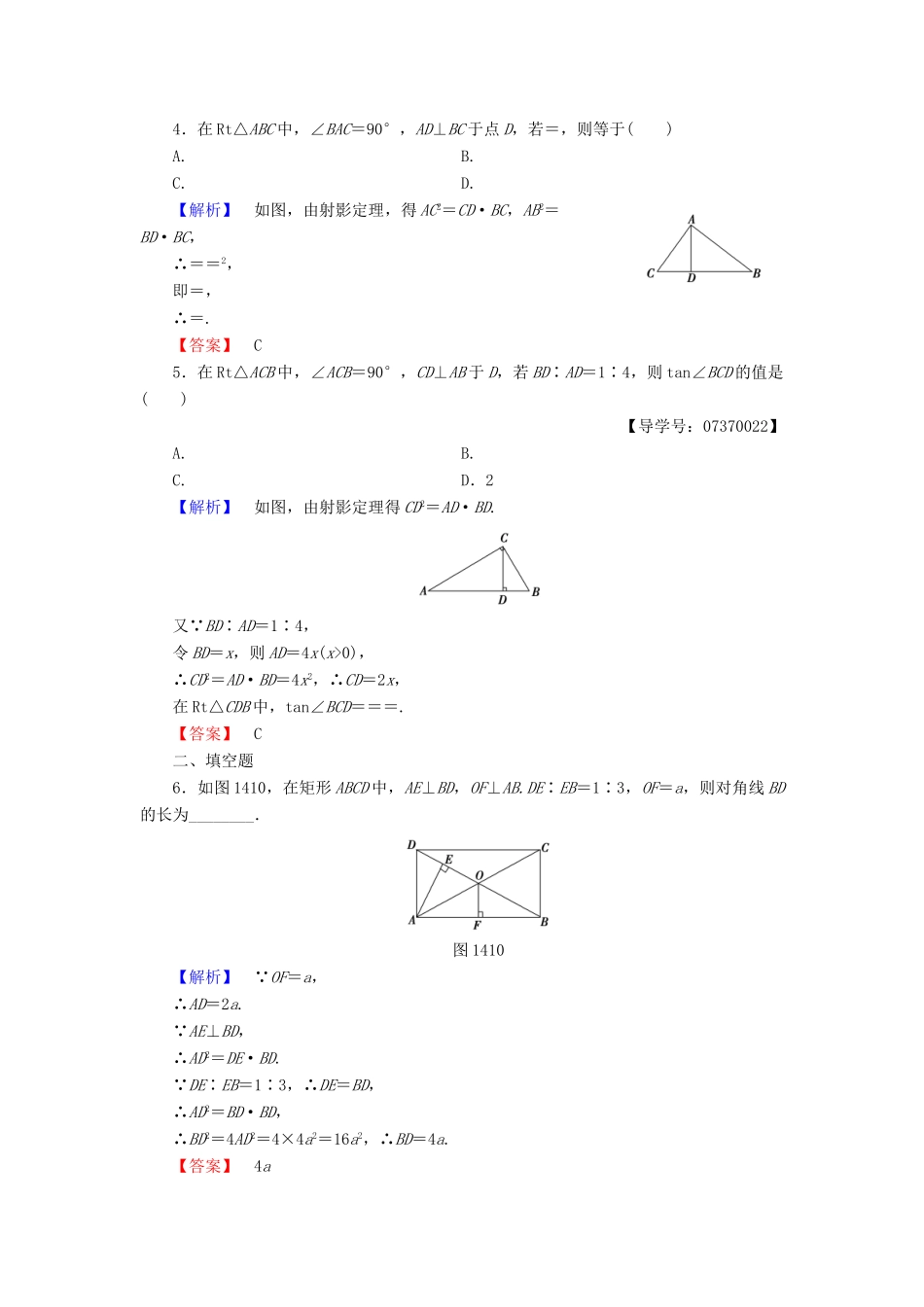
【课堂新坐标】2016-2017学年高中数学第一讲相似三角形的判定及有关性质学业分层测评5直角三角形的射影定理新人教A版选修4-1(建议用时:45分钟)[学业达标]一、选择题1.在△ABC中,∠ACB=90°,CD⊥AB于D,AD=3,BD=2,则AC∶BC的值是()A.3∶2B.9∶4C.∶D.∶【解析】如图,在Rt△ACB中,CD⊥AB,由射影定理知AC2=AD·AB,BC2=BD·AB,又∵AD=3,BD=2,∴AB=AD+BD=5,∴AC2=3×5=15,BC2=2×5=10.∴==,即AC∶BC=∶,故选C.【答案】C2.如图149所示,在△ABC中,∠ACB=90°,CD⊥AB,D为垂足,若CD=6,AD∶DB=1∶2,则AD的值是()图149A.6B.3C.18D.3【解析】由题意知∴AD2=18,∴AD=3.【答案】B3.一个直角三角形的一条直角边为3cm,斜边上的高为2.4cm,则这个直角三角形的面积为()【导学号:07370021】A.7.2cm2B.6cm2C.12cm2D.24cm2【解析】长为3cm的直角边在斜边上的射影为=1.8(cm),由射影定理知斜边长为=5(cm),∴三角形面积为×5×2.4=6(cm2).【答案】B4.在Rt△ABC中,∠BAC=90°,AD⊥BC于点D,若=,则等于()A.B.C.D.【解析】如图,由射影定理,得AC2=CD·BC,AB2=BD·BC,∴==2,即=,∴=.【答案】C5.在Rt△ACB中,∠ACB=90°,CD⊥AB于D,若BD∶AD=1∶4,则tan∠BCD的值是()【导学号:07370022】A.B.C.D.2【解析】如图,由射影定理得CD2=AD·BD.又∵BD∶AD=1∶4,令BD=x,则AD=4x(x>0),∴CD2=AD·BD=4x2,∴CD=2x,在Rt△CDB中,tan∠BCD===.【答案】C二、填空题6.如图1410,在矩形ABCD中,AE⊥BD,OF⊥AB.DE∶EB=1∶3,OF=a,则对角线BD的长为________.图1410【解析】∵OF=a,∴AD=2a.∵AE⊥BD,∴AD2=DE·BD.∵DE∶EB=1∶3,∴DE=BD,∴AD2=BD·BD,∴BD2=4AD2=4×4a2=16a2,∴BD=4a.【答案】4a7.如图1411,已知Rt△ABC的两条直角边AC,BC的长分别为3cm,4cm,以AC为直径的圆与AB交于点D,则BD=______cm.图1411【解析】连接CD,则CD⊥AB.由AC=3cm,BC=4cm,得AB=5cm.由射影定理得BC2=BD·BA,即42=5BD.所以BD=cm.【答案】8.已知在梯形ABCD中,DC∥AB,∠D=90°,AC⊥BC,AB=10cm,AC=6cm,则此梯形的面积为________.【解析】如图,过C点作CE⊥AB于E.在Rt△ACB中,∵AB=10cm,AC=6cm,∴BC=8cm,∴BE=6.4cm,AE=3.6cm,∴CE==4.8(cm),∴AD=4.8cm.又∵在梯形ABCD中,CE⊥AB,∴DC=AE=3.6cm.∴S梯形ABCD==32.64(cm2).【答案】32.64cm2三、解答题9.已知直角三角形周长为48cm,一锐角平分线分对边为3∶5两部分.(1)求直角三角形的三边长;(2)求两直角边在斜边上的射影的长.【解】(1)如图,设CD=3x,BD=5x,则BC=8x,过D作DE⊥AB,由题意可得,DE=3x,BE=4x,∴AE+AC+12x=48.又AE=AC,∴AC=24-6x,AB=24-2x,∴(24-6x)2+(8x)2=(24-2x)2,解得x1=0(舍去),x2=2,∴AB=20,AC=12,BC=16,∴三边长分别为20cm,12cm,16cm.(2)作CF⊥AB于F,∴AC2=AF·AB,∴AF===(cm).同理BF===(cm).∴两直角边在斜边上的射影长分别为cm,cm.10.如图1412所示,CD垂直平分AB,点E在CD上,DF⊥AC,DG⊥BE,点F,G分别为垂足.求证:AF·AC=BG·BE.图1412【证明】∵CD垂直平分AB,∴△ACD和△BDE均为直角三角形,并且AD=BD.又∵DF⊥AC,DG⊥BE,∴AF·AC=AD2,BG·BE=DB2.∵AD2=DB2,∴AF·AC=BG·BE.[能力提升]1.已知直角三角形中两直角边的比为1∶2,则它们在斜边上的射影比为()A.1∶2B.2∶1C.1∶4D.4∶1【解析】设直角三角形两直角边长分别为1和2,则斜边长为,∴两直角边在斜边上的射影分别为和.【答案】C2.已知Rt△ABC中,斜边AB=5cm,BC=2cm,D为AC上一点,DE⊥AB交AB于E,且AD=3.2cm,则DE=()A.1.24cmB.1.26cmC.1.28cmD.1.3cm【解析】如图,∵∠A=∠A,∴Rt△ADE∽Rt△ABC,∴=,DE===1.28.【答案】C3.如图1413所示,在Rt△ABC中,∠ACB=90°,CD⊥AB,AC=6,AD=3.6,则BC=__________.图1413【解析】由射影定理得,AC2=AD·AB,BC2=BD·AB,∴=,即BC2=.又∵CD2=AD·BD,∴BD=.∴BC2===64.∴BC=8.【答案】84.如图1414,已知BD,CE是△ABC的两条高,过点D的直线交BC和BA的延长线于G,H,交CE于F,且∠H=∠BCE,求证:GD2=FG·GH.图1414【证明】∵∠H=∠BCE,∠EBC=∠GBH,∴△BCE∽△BHG,∴∠BEC=∠BGH=90°,∴HG⊥BC.∵BD⊥AC,在Rt△BCD中,由射影定理得,GD2=BG·CG.①∵∠FGC=∠BGH=90°,∠GCF=∠H,∴△FCG∽△BHG,∴=,∴BG·CG=GH·FG.②由①②得,GD2=GH·FG.