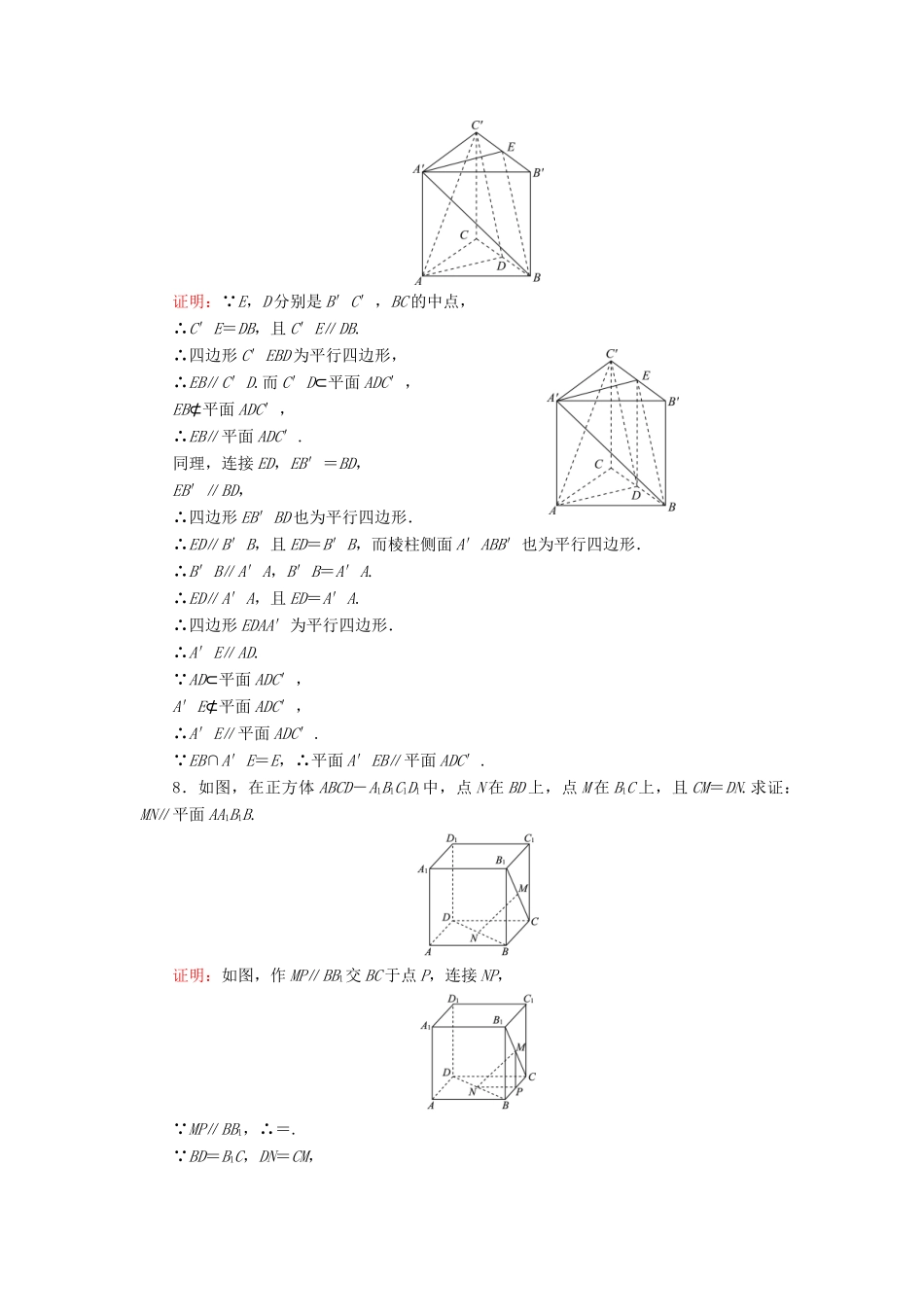
第二课时平面与平面平行课时跟踪检测[A组基础过关]1.一个平面内有无数条直线平行于另一个平面,那么这两个平面()A.一定平行B.一定相交C.平行或相交D.一定重合解析:根据平行的定义及平面平行的判定定理.答案:C2.若一条直线与两个平行平面中的一个平行,则这条直线与另一个平面的位置关系是()A.平行B.相交C.在平面内D.平行或在平面内答案:D3.下列结论中正确的是()A. a∥α,b∥α,∴a∥bB. a∥α,b⊂α,∴a∥bC. α∥β,a∥β,∴a∥αD. α∥β,a⊂β,∴a∥α答案:D4.已知m,n是不重合的直线,α,β,γ是不重合的平面,有下列命题:①若m⊂α,n∥α,则m∥n;②若m∥α,m∥β,则α∥β;③若α∩β=n,m∥n,则m∥α或m∥β;④若α∥β,α∥γ,则β∥γ.其中真命题的个数是()A.0个B.1个C.2个D.3个解析:①m与n还可能是异面;②α与β可能相交;③正确,m至少与α、β中的一个平面平行;④正确.答案:C5.如图,在正方体ABCD-A1B1C1D1中,E是AB的中点,F在CC1上,且CF=2FC1,点P是侧面AA1D1D(包括边界)上的动点,且PB1∥平面DEF,则tan∠ABP的取值范围是()A.B.[0,1]C.D.解析:过DEF三点作出正方体的截面DEMF,其中M在BB1上,且BM=BB1,取D1C1的中点T,连接B1T,可得B1T∥DE,过T作TS∥DF,则S在DD1上,且D1S=D1D,由平面ADD1A1∥平面BCC1B1,作SR∥FM,且AR=AA1,连接RB1,可得四边形RB1TS共面且平面RB1TS∥平面DEF,∴若PB1∥平面DEF,则P∈RS,当P在R时,tan∠ABP==,当P在S时,tan∠ABP==,∴tan∠ABP的取值范围为,故选D.答案:D6.已知α∥β,A,C∈α,B,D∈β,直线AB与CD交于点S,且AS=8,BS=9,CD=34,则CS的值为________.解析: α∥β,AB与CD相交可确定一个平面,∴AC∥BD,当交点S在α,β之间时,有=,∴=,∴CS=16.当交点S不在α,β之间时,如图所示,∴=,∴=,∴CS=272.答案:16或2727.如图在三棱柱ABC-A′B′C′中,点E,D分别是B′C′与BC的中点.求证:平面A′EB∥平面ADC′.证明: E,D分别是B′C′,BC的中点,∴C′E=DB,且C′E∥DB.∴四边形C′EBD为平行四边形,∴EB∥C′D.而C′D⊂平面ADC′,EB⊄平面ADC′,∴EB∥平面ADC′.同理,连接ED,EB′=BD,EB′∥BD,∴四边形EB′BD也为平行四边形.∴ED∥B′B,且ED=B′B,而棱柱侧面A′ABB′也为平行四边形.∴B′B∥A′A,B′B=A′A.∴ED∥A′A,且ED=A′A.∴四边形EDAA′为平行四边形.∴A′E∥AD. AD⊂平面ADC′,A′E⊄平面ADC′,∴A′E∥平面ADC′. EB∩A′E=E,∴平面A′EB∥平面ADC′.8.如图,在正方体ABCD-A1B1C1D1中,点N在BD上,点M在B1C上,且CM=DN.求证:MN∥平面AA1B1B.证明:如图,作MP∥BB1交BC于点P,连接NP, MP∥BB1,∴=. BD=B1C,DN=CM,∴MB1=NB,∴=,∴=,∴NP∥CD∥AB. NP⊄平面AA1B1B,AB⊂平面AA1B1B,∴NP∥平面AA1B1B. MP∥BB1,MP⊄平面AA1B1B,BB1⊂平面AA1B1B,∴MP∥平面AA1B1B.又 MP⊂平面MNP,NP⊂平面MNP,MP∩NP=P,∴平面MNP∥平面AA1B1B. MN⊂平面MNP,∴MN∥平面AA1B1B.[B组技能提升]1.在正方体ABCD-A1B1C1D1中,M为A1B1的中点,则下列结论中正确的有()①AB∥D1M;②DB1∥平面AMD1;③BC1∥平面AMD1;④平面ACD1∥平面A1C1B.A.1个B.2个C.3个D.4个解析:如图所示,AB与D1M为异面直线,①错;连接A1D交AD1于O点,连接OM,可知OM∥DB1,∴DB1∥平面AMD1,②正确;由ABCD-A1B1C1D1为正方体知BC1∥AD1,∴BC1∥平面AMD1,③正确;AC∥A1C1,AD1∥BC1,∴平面ACD1∥平面A1C1B,④正确.故选C.答案:C2.设α∥β,A∈α,B∈β,C是AB的中点,当A,B分别在平面α,β内运动时,那么所有的动点C()A.不共面B.当且仅当A,B分别在两条直线上移动时才共面C.当且仅当A,B分别在两条给定的异面直线上移动时才共面D.不论A,B如何移动,都共面解析:由面面平行的性质定理知,点C应在过AB中点,且平行于α(或β)的平面内,故选D.答案:D3.如图,在△ABC中,AB=5,AC=7,BC=,G是△ABC的重心.过G的平面α与BC平行,AB∩α=M,AC∩α=N,则MN=________.解析:...