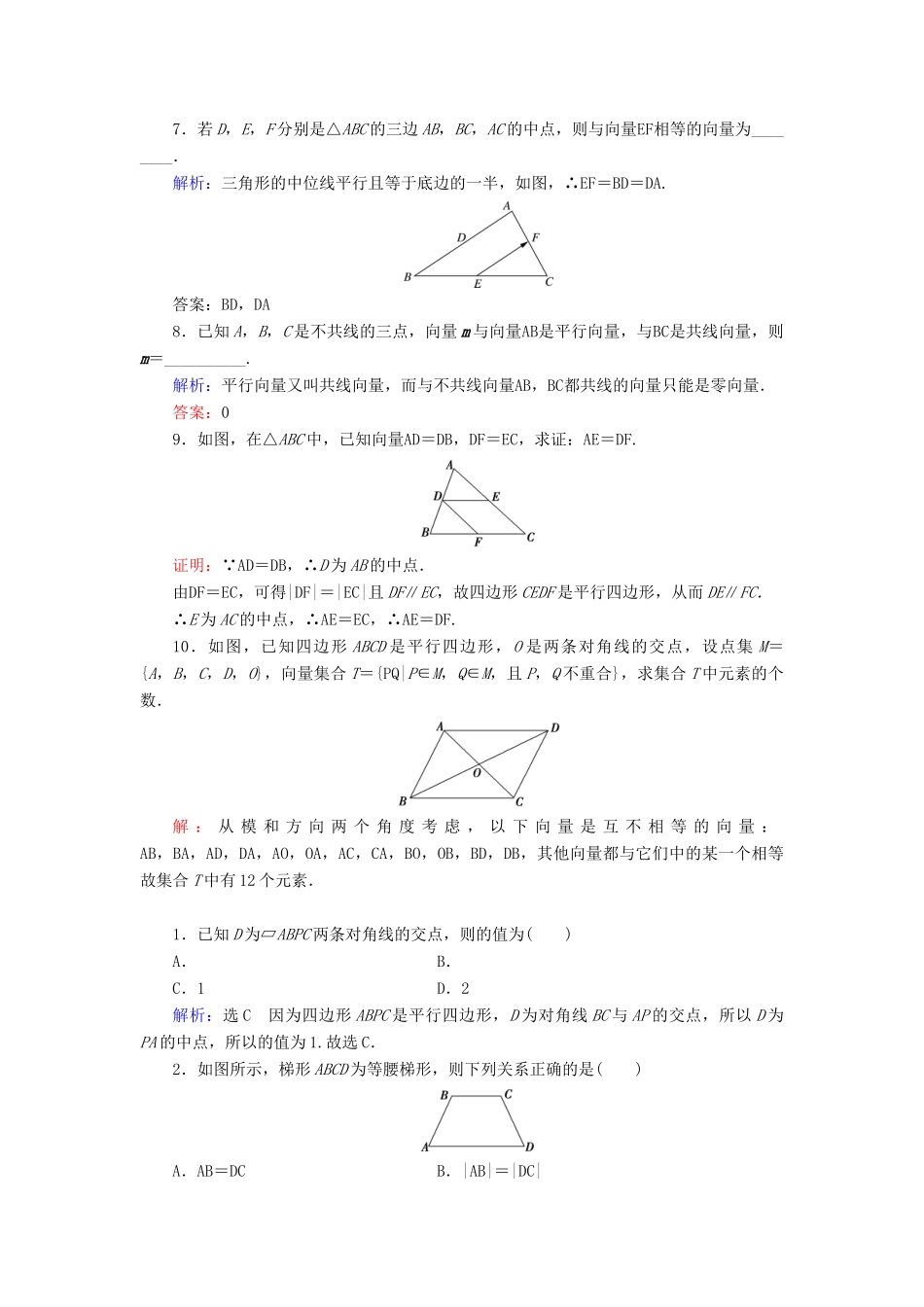
2.1平面向量的实际背景及基本概念课时分层训练1.下列说法中,正确的个数是()①时间、摩擦力、重力都是向量;②向量的模是一个正实数;③相等向量一定是平行向量;④向量a与b不共线,则a与b都是非零向量.A.1B.2C.3D.4解析:选B时间没有方向,不是向量,摩擦力、重力都是向量,故①错误;零向量的模为0,故②错误;相等向量的方向相同,因此一定是平行向量,故③正确;零向量与任一向量共线,故④正确.故选B.2.若a为任一非零向量,b的模为1,给出下列各式:①|a|>|b|;②a∥b;③|a|>0;④|b|=±1.其中正确的是()A.①④B.③C.①②③D.②③解析:选B|a|的大小不能确定,故①错误;两个非零向量的方向不确定,故②错误;向量的模是一个非负实数,故④错误;③正确.故选B.3.已知A={与a共线的向量},B={与a长度相等的向量},C={与a长度相等,方向相反的向量},其中a为非零向量,则下列说法中,错误的是()A.CAB.A∩B={a}C.CBD.A∩B{a}解析:选B因为A∩B中含有与a长度相等、方向相反的向量,所以B选项错误.4.在菱形ABCD中,∠DAB=120°,则以下说法错误的是()A.与AB相等的向量只有一个(不含AB)B.与AB的模相等的向量有9个(不含AB)C.BD的模恰为DA模的倍D.CB与DA不共线解析:选D两向量相等要求长度(模)相等,方向相同.两向量共线只要求方向相同或相反.D中CB与DA所在直线平行,向量方向相同,故共线.5.正n边形有n条边,它们对应的向量依次为a1、a2、a3,…,an,则这n个向量()A.都相等B.都共线C.都不共线D.模都相等解析:选D正n边形的边长相等,故这n个向量的模都相等.6.在四边形ABCD中,AB∥CD,|AB|≠|CD|,则四边形ABCD是________.答案:梯形7.若D,E,F分别是△ABC的三边AB,BC,AC的中点,则与向量EF相等的向量为________.解析:三角形的中位线平行且等于底边的一半,如图,∴EF=BD=DA.答案:BD,DA8.已知A,B,C是不共线的三点,向量m与向量AB是平行向量,与BC是共线向量,则m=__________.解析:平行向量又叫共线向量,而与不共线向量AB,BC都共线的向量只能是零向量.答案:09.如图,在△ABC中,已知向量AD=DB,DF=EC,求证:AE=DF.证明: AD=DB,∴D为AB的中点.由DF=EC,可得|DF|=|EC|且DF∥EC,故四边形CEDF是平行四边形,从而DE∥FC.∴E为AC的中点,∴AE=EC,∴AE=DF.10.如图,已知四边形ABCD是平行四边形,O是两条对角线的交点,设点集M={A,B,C,D,O},向量集合T={PQ|P∈M,Q∈M,且P,Q不重合},求集合T中元素的个数.解:从模和方向两个角度考虑,以下向量是互不相等的向量:AB,BA,AD,DA,AO,OA,AC,CA,BO,OB,BD,DB,其他向量都与它们中的某一个相等故集合T中有12个元素.1.已知D为▱ABPC两条对角线的交点,则的值为()A.B.C.1D.2解析:选C因为四边形ABPC是平行四边形,D为对角线BC与AP的交点,所以D为PA的中点,所以的值为1.故选C.2.如图所示,梯形ABCD为等腰梯形,则下列关系正确的是()A.AB=DCB.|AB|=|DC|C.AB>DCD.AB<DC解析:选B|AB|与|DC|表示等腰梯形两腰的长度,故相等.故选B.3.(2018·福建福州一中期末)设向量a0=,b0=,则下列结论中正确的是()A.a0=b0B.a0=-b0C.|a0|+|b0|=2D.a0∥b0解析:选C由题意知a0,b0是单位向量,所以|a0|=1,|b0|=1,所以|a0|+|b0|=2.故选C.4.如图是3×4的格点图(每个小方格都是单位正方形),若起点和终点都在方格的顶点处,则与AB平行且模为的向量共有()A.12个B.18个C.24个D.36个解析:选C由题意,知与AB平行且模为的向量共有24个.故选C.5.把同一平面内所有模不小于1且不大于2的向量的起点移到同一点O,则这些向量的终点构成的图形的面积等于________.解析:这些向量的终点构成的图形是一个圆环,其面积为π×22-π×12=3π.答案:3π6.(2019·北京东城期末)给出下列条件:①a=b;②|a|=|b|;③a与b方向相反;④|a|=0或|b|=0.其中能使a∥b成立的条件是________(填序号).解析:若a=b,则a与b大小相等且方向相同,所以a∥b;若|a|=|b|,则a与b的大小相等,而方向不确定,因此不一定有a∥b;方向相同或相反的...