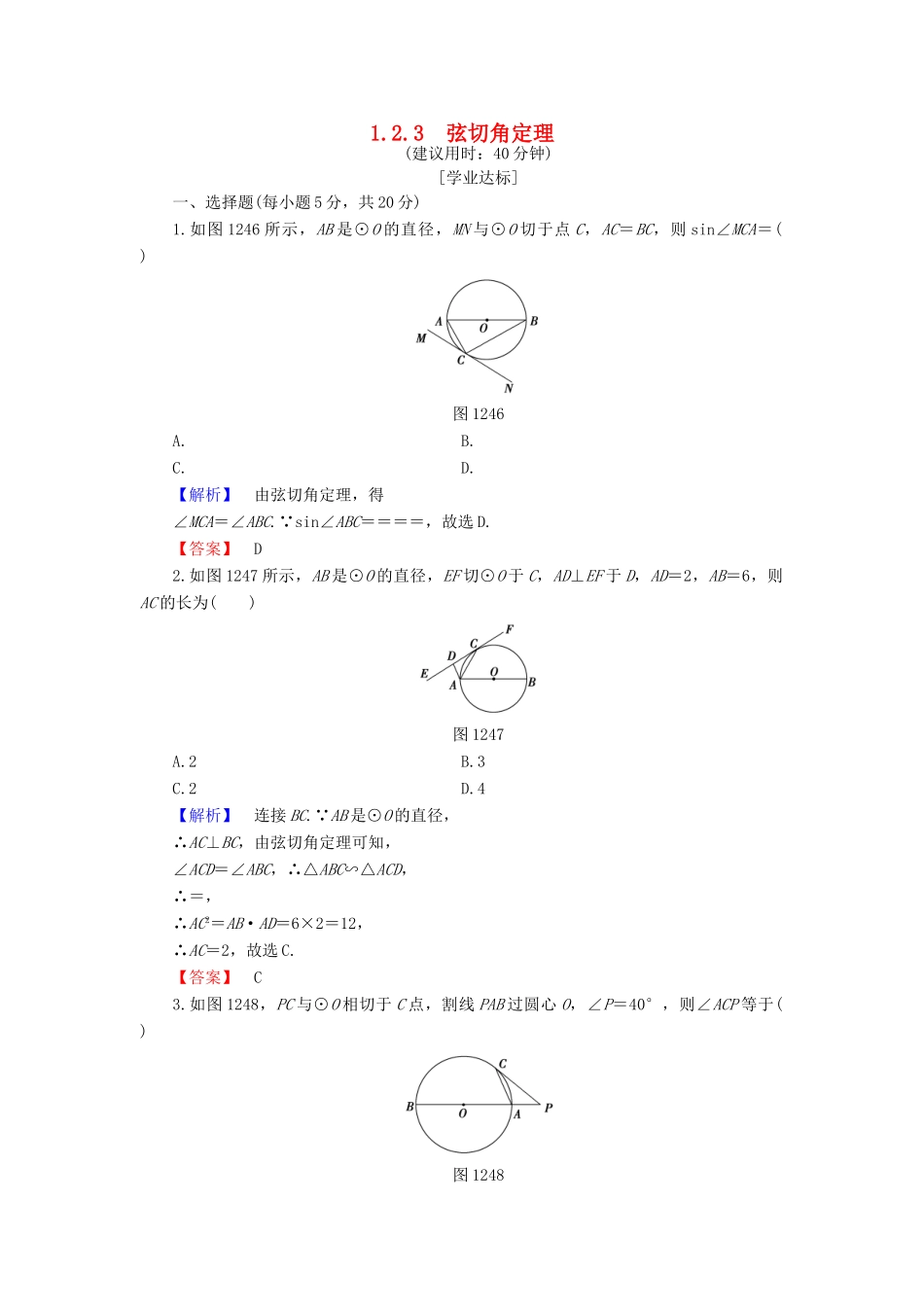
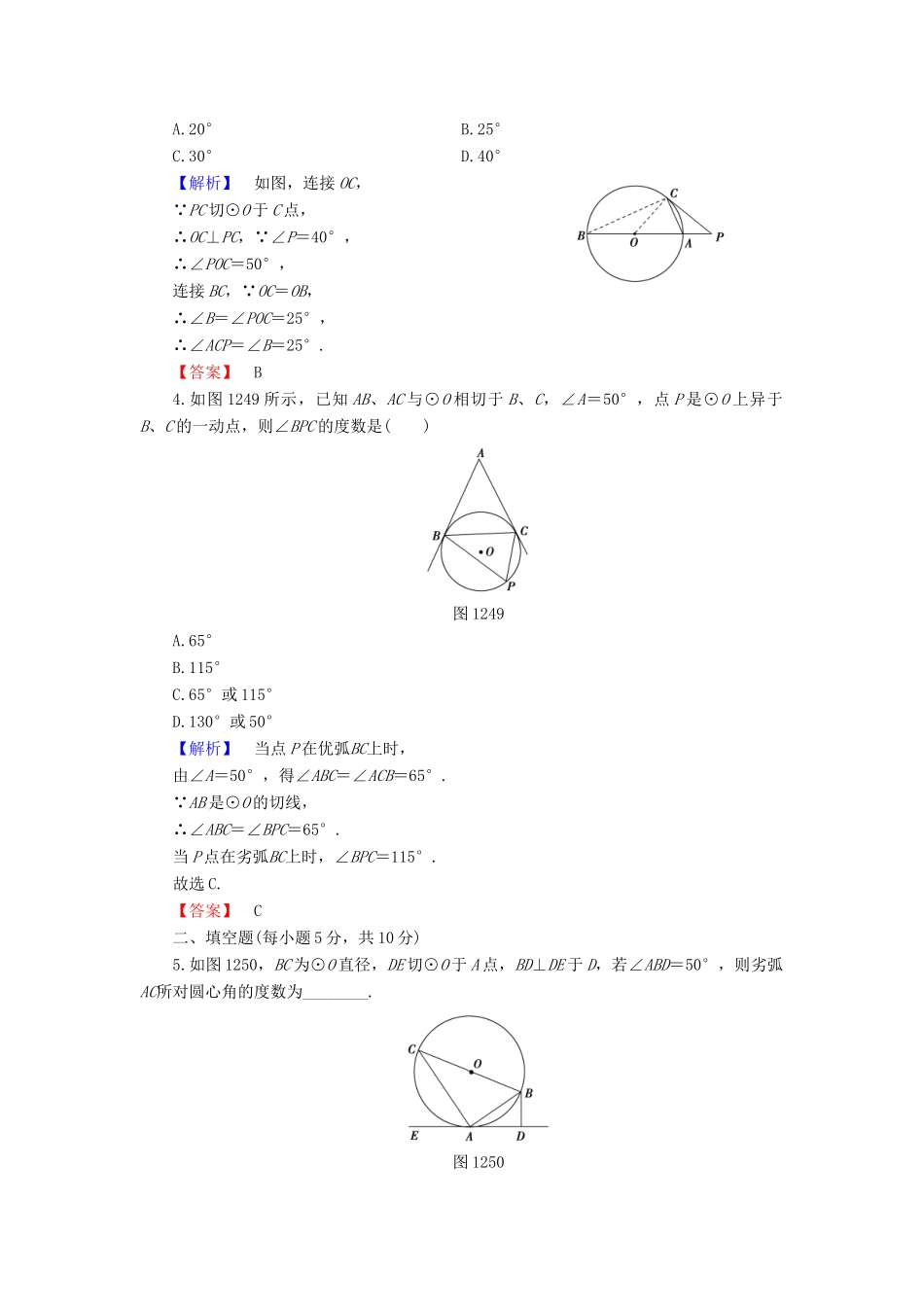
1.2.3弦切角定理(建议用时:40分钟)[学业达标]一、选择题(每小题5分,共20分)1.如图1246所示,AB是⊙O的直径,MN与⊙O切于点C,AC=BC,则sin∠MCA=()图1246A.B.C.D.【解析】由弦切角定理,得∠MCA=∠ABC.∵sin∠ABC====,故选D.【答案】D2.如图1247所示,AB是⊙O的直径,EF切⊙O于C,AD⊥EF于D,AD=2,AB=6,则AC的长为()图1247A.2B.3C.2D.4【解析】连接BC.∵AB是⊙O的直径,∴AC⊥BC,由弦切角定理可知,∠ACD=∠ABC,∴△ABC∽△ACD,∴=,∴AC2=AB·AD=6×2=12,∴AC=2,故选C.【答案】C3.如图1248,PC与⊙O相切于C点,割线PAB过圆心O,∠P=40°,则∠ACP等于()图1248A.20°B.25°C.30°D.40°【解析】如图,连接OC,∵PC切⊙O于C点,∴OC⊥PC,∵∠P=40°,∴∠POC=50°,连接BC,∵OC=OB,∴∠B=∠POC=25°,∴∠ACP=∠B=25°.【答案】B4.如图1249所示,已知AB、AC与⊙O相切于B、C,∠A=50°,点P是⊙O上异于B、C的一动点,则∠BPC的度数是()图1249A.65°B.115°C.65°或115°D.130°或50°【解析】当点P在优弧BC上时,由∠A=50°,得∠ABC=∠ACB=65°.∵AB是⊙O的切线,∴∠ABC=∠BPC=65°.当P点在劣弧BC上时,∠BPC=115°.故选C.【答案】C二、填空题(每小题5分,共10分)5.如图1250,BC为⊙O直径,DE切⊙O于A点,BD⊥DE于D,若∠ABD=50°,则劣弧AC所对圆心角的度数为________.图1250【解析】∵BD⊥DE,∠ABD=50°,∴∠BAD=40°.∵AD为⊙O的切线,∴∠C=40°,又∵BC为⊙O的直径,∴∠CAB=90°,∴∠CBA=50°,∴AC所对圆心角的度数为100°.【答案】100°6.(广东高考)如图1251,过圆O外一点P分别作圆的切线和割线交圆于A,B,且PB=7,C是圆上一点使得BC=5,∠BAC=∠APB,则AB=________.图1251【解析】由弦切角定理得∠PAB=∠ACB,又因为∠BAC=∠APB,所以△PAB∽△ACB,可得=,将PB=7,BC=5代入得AB=.【答案】三、解答题(每小题10分,共30分)7.如图1252所示,△ABT内接于⊙O,过点T的切线交AB的延长线于点P,∠APT的平分线交BT、AT于C、D.图1252求证:△CTD为等腰三角形.【导学号:61650016】【证明】∵PD是∠APT的平分线,∴∠APD=∠DPT.又∵PT是圆的切线,∴∠BTP=∠A.又∵∠TDC=∠A+∠APD,∠TCD=∠BTP+∠DPT,∴∠TDC=∠TCD,∴△CTD为等腰三角形.8.如图1253,AD是△ABC的角平分线,经过点A、D的⊙O和BC切于D,且AB、AC与⊙O相交于点E、F,连接DF.图1253(1)求证:EF∥BC;(2)求证:DF2=AF·BE.【证明】(1)∵⊙O切BC于D,∴∠CAD=∠CDF.∵AD是△ABC的角平分线,∴∠BAD=∠CAD,又∵∠BAD=∠EFD,∴∠EFD=∠CDF,∴EF∥BC.(2)如图,连接DE,∵⊙O切BC于D,∴∠BAD=∠BDE,由(1)可得∠BDE=∠FAD,又∵⊙O内接四边形AEDF,∴∠BED=∠DFA,∴△BED∽△DFA,∴=.又∵∠BAD=∠CAD,∴DE=DF,∴DF2=AF·BE.[能力提升]9.如图1254,△ABC内接于圆O,AB=AC,直线MN切圆O于点C,弦BD∥MN,AC与BD相交于点E.图1254(1)求证:△ABE≌△ACD;(2)若AB=6,BC=4,求AE.【解】(1)证明:由已知得∠ABE=∠ACD,∠BAE=∠EDC,又∵BD∥MN,∴∠DCN=∠EDC,∴∠BAE=∠DCN.又直线MN切圆O于点C,∴∠CAD=∠DCN.∴∠CAD=∠BAE.又AB=AC,∴△ABE≌△ACD.(2)由于△ABE≌△ACD,则BE=CD,由(1)得∠CAD=∠BAE,∴BC=CD.∴BE=CD=4.在△ABE和△CDE中,∠BAE=∠EDC,∠EBA=∠ECD,∴△ABE∽△DCE.∴=.∴=.∴=,解得AE=.