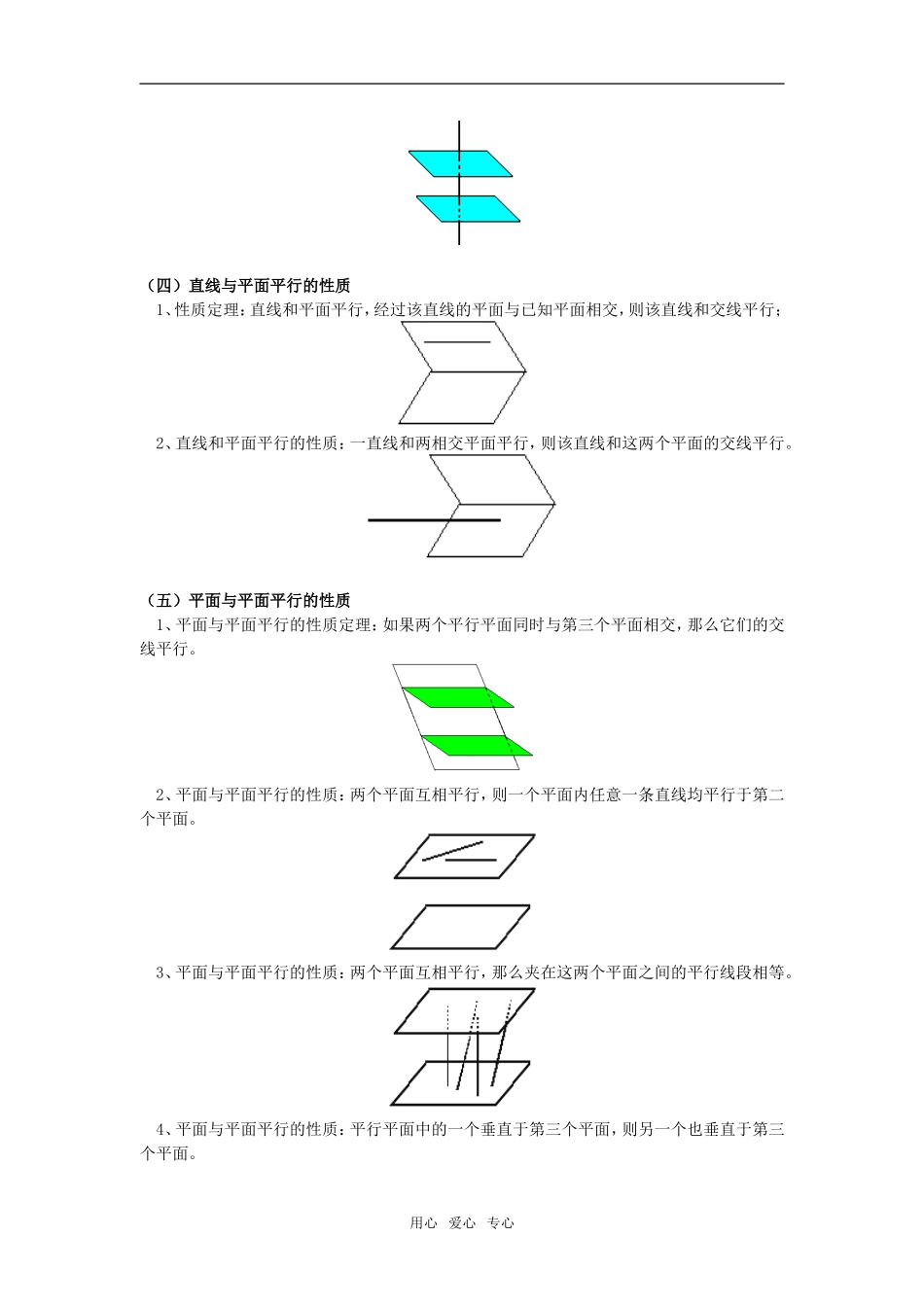
高一数学空间平行关系北师大版【本讲教育信息】一、教学内容:空间平行关系的判定与性质,包括:1、线线平行;2、线面平行;3、面面平行。二、学习目标1、掌握空间平行关系的判定与性质定理并会应用;2、通过对定理的学习,培养和发展空间想象能力、推理论证能力和运用图形进行交流的能力;3、通过操作确认、直观感知,培养几何直观能力;4、通过典型例子的分析和探索活动,理解数学概念和结论,体会蕴含其中的思想方法。三、知识要点(一)直线与直线平行的判定方法1、利用定义:在同一个平面内,不相交的两条直线互相平行;2、利用平行公理:空间中平行于同一条直线的两条直线互相平行;3、利用直线与平面平行的性质定理:直线和平面平行,经过该直线的平面与已知平面相交,则该直线和交线平行;4、利用平面和平面平行的性质定理:两个平面互相平行,和第三个平面相交,它们的交线互相平行;5、利用直线和平面垂直的性质:垂直于同一个平面的两条直线互相平行;6、利用直线和平面平行的性质:一直线和两相交平面平行,则该直线和这两个平面的交线平行。用心爱心专心(二)直线与平面平行的判定方法1、利用定义:直线与平面无公共点,则该直线和该平面平行;2、利用直线与平面平行的判定定理:平面外一条直线和平面内一条直线平行,则该直线和该平面平行(线线平行,则线面平行)。3、利用平面和平面平行的性质:两个平面互相平行,则一个平面内任意一条直线都平行于第二个平面。(三)平面和平面平行的判定方法1、利用定义:两个平面没有公共点,则这两个平面平行;2、利用平面与平面平行的判定定理:一个平面内有两条相交直线分别与另一个平面内两条相交直线平行,则这两个平面平行;3、利用平面与平面平行的判定:一个平面内有两条相交直线分别平行于另一个平面,则这两个平面平行;4、利用平面与平面平行的传递性:平行于同一个平面的两个平面互相平行.5、利用直线与平面垂直的性质:垂直于同一条直线的两个平面互相平行;用心爱心专心(四)直线与平面平行的性质1、性质定理:直线和平面平行,经过该直线的平面与已知平面相交,则该直线和交线平行;2、直线和平面平行的性质:一直线和两相交平面平行,则该直线和这两个平面的交线平行。(五)平面与平面平行的性质1、平面与平面平行的性质定理:如果两个平行平面同时与第三个平面相交,那么它们的交线平行。2、平面与平面平行的性质:两个平面互相平行,则一个平面内任意一条直线均平行于第二个平面。3、平面与平面平行的性质:两个平面互相平行,那么夹在这两个平面之间的平行线段相等。4、平面与平面平行的性质:平行平面中的一个垂直于第三个平面,则另一个也垂直于第三个平面。用心爱心专心四、考点与典型例题考点一判定直线与直线平行例1、已知平面α∩β=m,直线a//α,a//β,求证:a//m。证明:过a作一平面与α交于直线b,由线面平行的性质可知:a//b;过a作另一平面与β交于直线c,则:a//c。由平行公理可知:b//c,故b//β.由线面平行的性质可知:b//m.由平行公理,a//m。【说明】判定空间关系的主要思路有三种,一是利用判定定理和相关结论,二是反证法(常利用定义),三是同一法,并且凡是用反证法可以证明的都可以用同一法证明。而且一般地,每个这样的题目都可以同时使用这三种方法.同一法的主要过程是:欲证某几何图形M具备某性质,可以先作一个图形M′具备这种性质,然后证明所作图形M′与待证图形M是同一个图形,因M′具备这种性质,故M也具备该性质。如本题可用同一法证明如下:证明:在m上取一点A,过a、A作一平面分别交α、β于e、f,则e//a,f//a,即过直线外一点有两条直线与之平行,因此e、f重合,记为l;又e在α上,f在β上,且e、f重合于l,故l是α、β的交线,故l与m重合。因l//a,故m//a。考点二判定直线与平面平行例2、平面α外的两条直线a//b,且a//α,求证:b//α.证明:因a//α,过a作一平面与α交于直线m,则由直线与平面平行的性质可知:a//m.又因a//b,a//m,故b//m,由线面平行的判定定理可知:b//α.考点三:线面平行的性质例3、如图,ABCD是平行四边形,点P是平面ABCD外一点,M是PC...