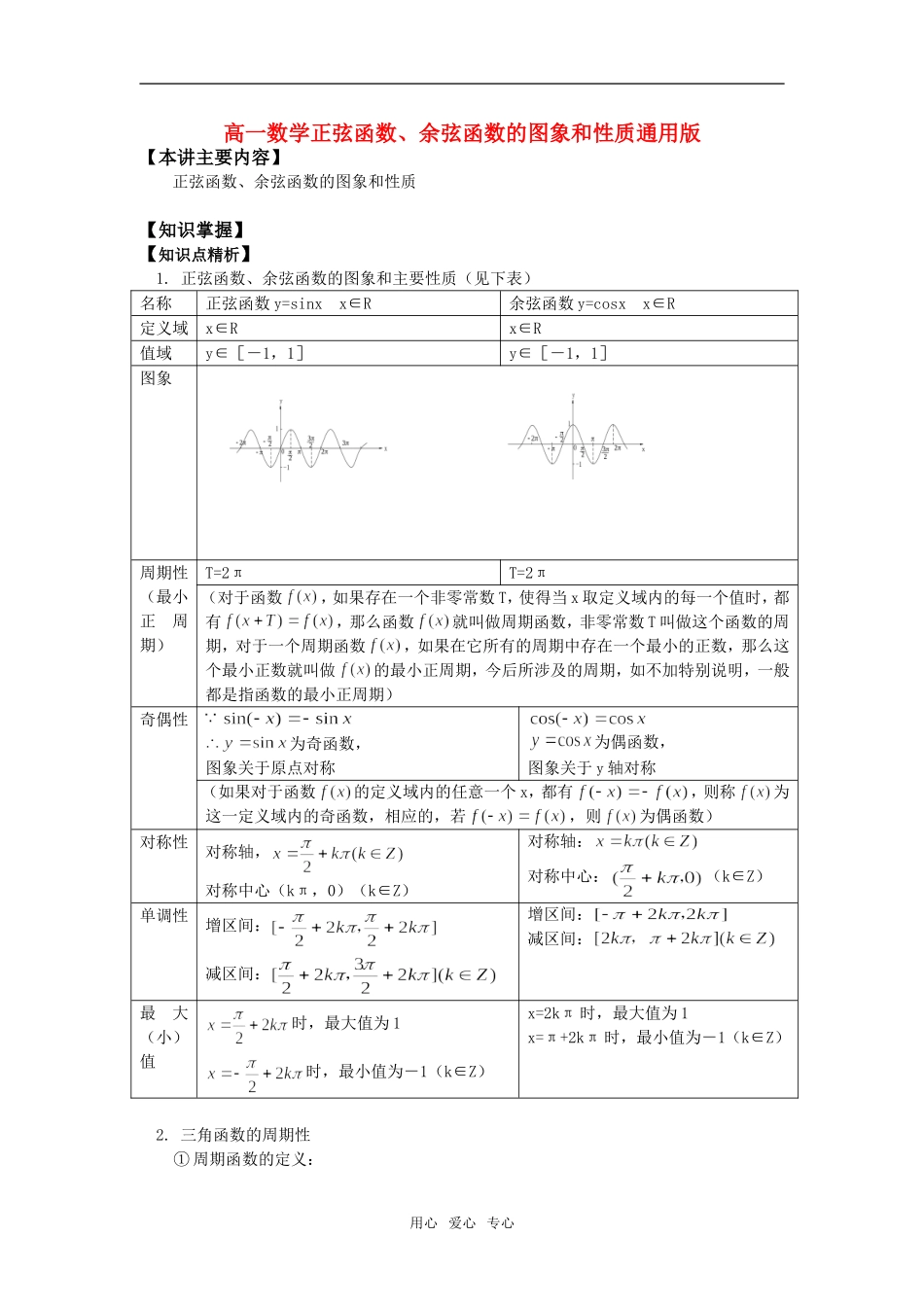
高一数学正弦函数、余弦函数的图象和性质通用版【本讲主要内容】正弦函数、余弦函数的图象和性质【知识掌握】【知识点精析】1.正弦函数、余弦函数的图象和主要性质(见下表)名称正弦函数y=sinxx∈R余弦函数y=cosxx∈R定义域x∈Rx∈R值域y∈[-1,1]y∈[-1,1]图象周期性(最小正周期)T=2πT=2π(对于函数,如果存在一个非零常数T,使得当x取定义域内的每一个值时,都有,那么函数就叫做周期函数,非零常数T叫做这个函数的周期,对于一个周期函数,如果在它所有的周期中存在一个最小的正数,那么这个最小正数就叫做的最小正周期,今后所涉及的周期,如不加特别说明,一般都是指函数的最小正周期)奇偶性为奇函数,图象关于原点对称为偶函数,图象关于y轴对称(如果对于函数的定义域内的任意一个x,都有,则称为这一定义域内的奇函数,相应的,若,则为偶函数)对称性对称轴,对称中心(kπ,0)(k∈Z)对称轴:对称中心:(k∈Z)单调性增区间:减区间:增区间:减区间:最大(小)值时,最大值为1时,最小值为-1(k∈Z)x=2kπ时,最大值为1x=π+2kπ时,最小值为-1(k∈Z)2.三角函数的周期性①周期函数的定义:用心爱心专心一般地,对于函数,若存在常数T(T≠0),使得当x取它定义域内的每一个值时,都有,则函数就叫做周期函数,T叫做的周期。②最小正周期:若的所有周期中存在一个最小正数,则称这个最小正数为最小正周期。③正弦函数,余弦函数都是周期函数,2kπ(k∈Z且k≠0)都是它们的周期,最小正周期是2π。(注意:以后若不加说明,周期都是指函数的最小正周期)④一般地:函数,x∈R及函数,x∈R(其中A,ω,为常数,且A≠0,ω>0)的周期为3.用“五点法”作正弦函数和余弦函数的简图用几何法做出图象比较精确,但画图较繁。因此,在精度要求不太高时,我们常常采用“五点作图法”。(1)正弦函数的图象中,五个关键点是:(0,0)(,1)(π,0)(,-1)(2π,0)(2)余弦函数的图象中,五个关键点是:(0,1)(,0)(π,-1)(,0)(2π,1)因此,在精度要求不太高时,我们常常先描出五个关键点,然后用光滑的曲线依次连接起来,就分别得到了y=sinx,y=cosx,x∈[0,2π]的简图,这种作图法称为“五点法”。【解题方法指导】例1.求下列函数的定义域。(1)(2)用心爱心专心分析:应先列出使函数有意义的几个不等式,然后利用数轴或者图象求出它们的公共解集。解:(1)要使此函数有意义,必须即如图所示∴函数的定义域是:(2)依题意可知:,即∴函数的定义域为说明:确定三角函数的定义域的依据是:①正、余弦函数自身的定义域(大前提),见第一页表格。②若函数是分式函数,则分母不为零。③若函数是偶次根式,则被开方式非负。④若函数是形如的函数,则其定义域由及a>0且a≠1共同确定。例2.求下列函数的最大值与最小值。(1)(2)分析(1):可利用y=sinx的值域求解,特别注意前面有“-”号。解(1):当,即时用心爱心专心取最大值1,从而当,即时取最小值-1,从而分析(2):利用三角函数的恒等变形公式将原函数化为关于sinx的二次函数,把问题转化为二次函数求最值问题。解(2):∴当sinx=-1时,即时,当sinx=1时,即时,评述:题型①(如第1小题)求函数的最值或值域主要是利用y=sinx与y=cosx的有界性,以及复合函数的有关性质求解。题型②(如第2小题)求函数的最值或值域是将函数转化为二次函数型求解。注意:第2小题配方后的式子为,其中,而,所以sinx取不到,故y就取不到最大值。同学们很容易在此犯错误,请注意。例3.求下列函数的单调递增区间。(1)(2)分析(1):根据基本函数的单调性来求解。解(1):y=cos2x的单调递增区间由下面不等式确定:故函数的单调递增区间是分析(2):原函数可以化为这样变形是为了保证“x”的系数为“正”再利用基本函数y=sinx的单调性来求解。解(2):由用心爱心专心递减区间为的递增区间由下面不等式确定,即:故:函数的单调递增区间是评述:求形如或(其中A≠0,ω>0)的函数的单调区间,可以通过解不等式的方法去解答,列不等式的原则是:①把“”(ω>0)视为一个“整体”...