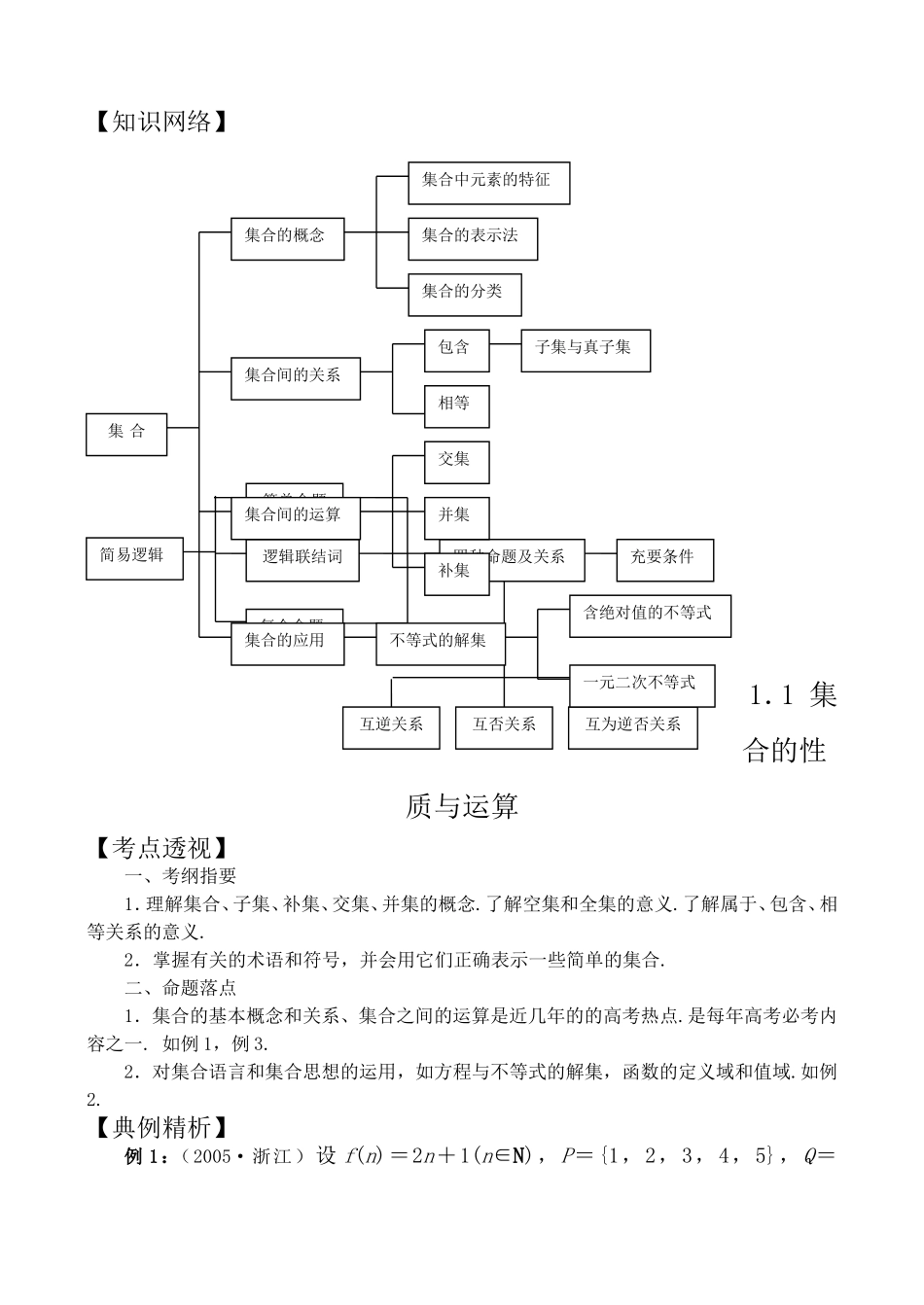
高一数学学案目录性质与运算模块一集合1.1集合的性质与运算1.2命题1.3充分必要条件1.4反证法模块二函数2.1映射、函数的解析式(定义域)2.2反函数2.3函数的单调性与奇偶性2.4二次函数2.5指数函数与对数函数2.6函数的图象2.7函数的值域与最大值2.8函数的实际应用模块三数列3.1数列的概念3.2等差数列的通项与前n项的和3.3等比数列的通项与前n项的和3.4数列的的前n项的和3.5递推数列模块四三角函数4.1三角函数的概念4.2同角三角函数间的关系及诱导公式4.3两角和与差的三角函数4.4三角函数的图象4.5三角函数的定义域、值域、最值4.6三角函数的周期性、奇偶性、单调性模块五平面向量5.1平面向量的基本运算、坐标运算5.2平面向量的数量积5.3线段的定比分点及平移5.4正、余弦定理的应用第一章集合与简易逻辑【知识网络】1.1集合的性质与运算【考点透视】一、考纲指要1.理解集合、子集、补集、交集、并集的概念.了解空集和全集的意义.了解属于、包含、相等关系的意义.2.掌握有关的术语和符号,并会用它们正确表示一些简单的集合.二、命题落点1.集合的基本概念和关系、集合之间的运算是近几年的的高考热点.是每年高考必考内容之一.如例1,例3.2.对集合语言和集合思想的运用,如方程与不等式的解集,函数的定义域和值域.如例2.【典例精析】例1:(2005·浙江)设f(n)=2n+1(n∈N),P={1,2,3,4,5},Q=简易逻辑简单命题逻辑联结词复合命题四种命题及关系充要条件互否关系互为逆否关系互逆关系集合集合的概念集合中元素的特征集合的表示法集合的分类集合间的关系包含相等子集与真子集交集并集补集集合间的运算集合的应用不等式的解集含绝对值的不等式一元二次不等式{3,4,5,6,7},记={n∈N|f(n)∈P},={n∈N|f(n)∈Q},则(∩)∪(∩)=()A.{0,3}B.{1,2}.C.(3,4,5)D.{1,2,6,7}解析:={0,1,2},={n∈N|n≥2},={1,2,3},={n∈N|n=0或n≥4},故∩={0},∩={3},得(∩)∪(∩)={0,3},答案:A.例2:(2005•上海)已知集合,,则等于()A.B.C.D.解析:,=.D:B.例3:设全集是I的子集,若,就称集对(A,B)为好集,那么所有好集的个数为().A.6!B.C.D.解析:要使,必须满足集合A,B中都含有元素1,2,3,且对全集中的其它6个元素4,5,6,7,8,9中的每个元素,要么在集合A中,要么在集合B中或不在集合A、B中,这三种情况只能选其一,于是这6个元素所处集合的不同情况为.而这6个元素所处不同集合的个数即为好集的不同个数.答案:D.【常见误区】1.解题粗心大意,不考虑元素的特征,对数集,点集理解有误;如就表示完全不同的三个集合,如不注意它们的区别,很容易出错.2.不能准确把握子集、真子集、相等、补集等相关概念,在转化命题时往往出现错误;3.对空集理解不正确或忽视空集在解题中的地位和作用而产生错误.【基础演练】1.(2005•全国1)设为全集,是的三个非空子集,且,则下面论断正确的是()A.B.C.D.2.设全集U={-2,-1,0,1,2},A={-2,-1,0},B={0,1,2},则(UA)∩B=()A.{0}B.{-2,-1}C.{1,2}D.{0,1,2}3.(2005•全国2)已知集合,,则为()A.或B.或C.或D.或4.(2006•陕西)已知集合P={x∈N|1≤x≤10},集合Q={x∈R|x2+x-6≤0},则P∩Q等于()A.{2}B.{1,2}C.{2,3}D.{1,2,3}5.(2005•重庆)集合R|,则=.6.(2004•上海)设集合A={5,log2(a+3)},集合B={a,b}.若A∩B={2},则A∪B=7.(2004•辽宁)设全集U=R(1)解关于x的不等式(2)记A为(1)中不等式的解集,集合,若(A)∩B恰有3个元素,求a的取值范围.8.(2004•上海)记函数=的定义域为A,g(x)=lg[(x-a-1)(2a-x)](a<1)的定义域为B.(1)求A;(2)若BA,求实数a的取值范围.9.设集合A={x||x-a|<2},B={x|<1},若AB,求实数a的取值范围.1.2命题【考点透视】一、考纲指要1.理解逻辑联结词“或”、“且”、“非”的含义.2.理解四种命题及其相互关系.二、命题落点1.对命题真假的判断或考查一命题的否定与非命题如例1,例2,例3.【典例精析】例1(2005•天津)给出下列三个命题①若,则;②若正整数和满足,则;③设是圆上的任意一点,圆以为圆...