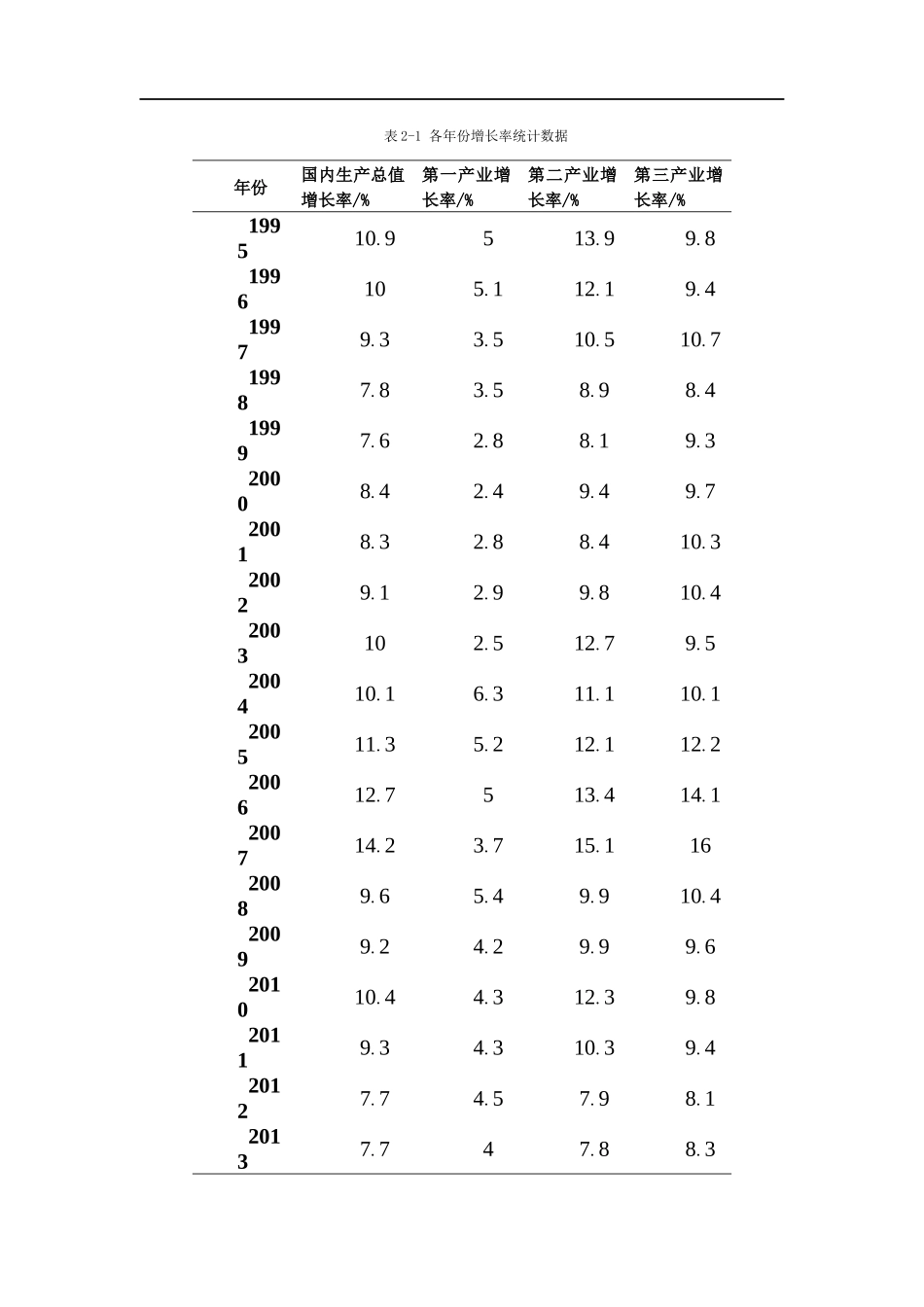
多元线性回归在国内生产总值(GDP)增长率预测中的应用摘要:产业结构变动与经济增长是分不开的。经济增长率的高低体现了一个国家或地区在一定时期内经济总量的增长速度,也是衡量一个国家或地区总体经济实力增长速度的标志。为了更好的了解我国各产业增长率对我国国内生产总值增长率的影响,从《中国统计年鉴》中选取数据,通过运用EXCEL软件对以上数据进行了多元线性回归分析,通过显著性分析,最终得到了能够比较准确反映国内生产总值增长率与各产业增长率关系的最佳模型,对下一年生产率进行预测。关键词:国内生产总值增长率;EXCEL;多元线性回归;预测1问题的提出与分析产业结构变动与经济增长是分不开的。经济增长通常是指在一个较长的时间跨度上,一个国家人均产出(或人均收入)水平的持续增加。经济增长率的高低体现了一个国家或地区在一定时期内经济总量的增长速度,也是衡量一个国家或地区总体经济实力增长速度的标志。它构成了经济发展的物质基础,而产业结构的调整与优化升级对于经济增长乃至经济发展至关重要。为此,了解国家税收收入的影响因素具有重要作用。然而,影响国家国内生产总值的因素较多,如何从中找出关键的几个因素,并建立最能反映实际情况的数学模型,是我们必须要解决的问题。查阅各种资料了解到,结合实际经验,本文选取了就业人数,国内生产总值增长率,第一产业增长率,第二产业增长率,第三产业增长率3个因素作为影响国内生产总值增长率的因子,并以国内生产总值增长率为因变量,对该问题进行了详细分析。2数据描述本文选取了《中国统计年鉴》中1995年-2013年的数据,以国内生产总值(GDP)增长率、第一产业增长率、第二产业增长率、第三产业增长率等4个为研究对象,得出数据表格如表2-1所示。表2-1各年份增长率统计数据年份国内生产总值增长率/%第一产业增长率/%第二产业增长率/%第三产业增长率/%199510.9513.99.81996105.112.19.419979.33.510.510.719987.83.58.98.419997.62.88.19.320008.42.49.49.720018.32.88.410.320029.12.99.810.42003102.512.79.5200410.16.311.110.1200511.35.212.112.2200612.7513.414.1200714.23.715.11620089.65.49.910.420099.24.29.99.6201010.44.312.39.820119.34.310.39.420127.74.57.98.120137.747.88.3数据来源:中国统计年鉴-2014http://www.stats.gov.cn/tjsj/ndsj/2014/indexch.htm3模型建立3.1提出假设条件,明确概念,引入参数假设:(i)解释变量X1,X2,X3是可控制的,非随机变量;(ii)随机物产项具有零均值和同方差的性质;(iii)符合正态分布。本文选取国内生产总值增长率为Y,选取第一产业增长率为X1,选取第二产业增长率为X2,选取第二产业增长率为X3。3.2模型构建对于因变量Y,有三个影响因素X1,X2和X3,则因变量和自变量之间的多元线性回归模型为:(3.1)(3.2)其中:,,,为回归系数为随机误差为例便于理论分析和计算机操作,将模型设为的实验数据,且满足(3.3)记β=(β0,β1,···,β3)T,Y=(y1,y2,···,yn)T,ε=(ε1,ε2,···,εn)T,(数据中n=19,为例方便标记采用n)则(3,4)式表示为{Y=Xβ+εεNn(0,σ2In)(3.4)3.3模型求解利用最小二乘法,得到β的LS估计为^β=(XTX)−1XTY(3.5)从而,多元线性回归方程为^Y=X^β=X(XTX)−1XTY(3.6)4计算方法设计与计算机实现4.1算法设计用EXCEL软件对自变量和因变量进行回归分析,得到回归方程;然后根据所得到的数据,如果存在影响不显著的变量则剔除,没有则不用剔除,得到符合实际情况的多元线性回归方程,对回归方程采用F检验对整体的显著性进行检验,采用t检验法进行回归系数显著性进行检验;最后用方程对下一年的数据进行预测。4.2模型求解与显著性检验(1)利用EXCEl2013对表2-1中的数据按照步骤进行回归分析,可以得到图4-1~4-3中的数据,图4-1回归统计分析图4-2多元线性回归方差分析表图4-3回归系数估计及检验统计值表由图4-3可知,回归系数的最小二乘估计值为:由此得到经验回归方程为:(5.1)(2)拟合优度检验由以上回归结果,、的值越接近1,表明回归直线对观测值的拟合效果越好;反之,、的值越接近0,表明回归直线对观测值...