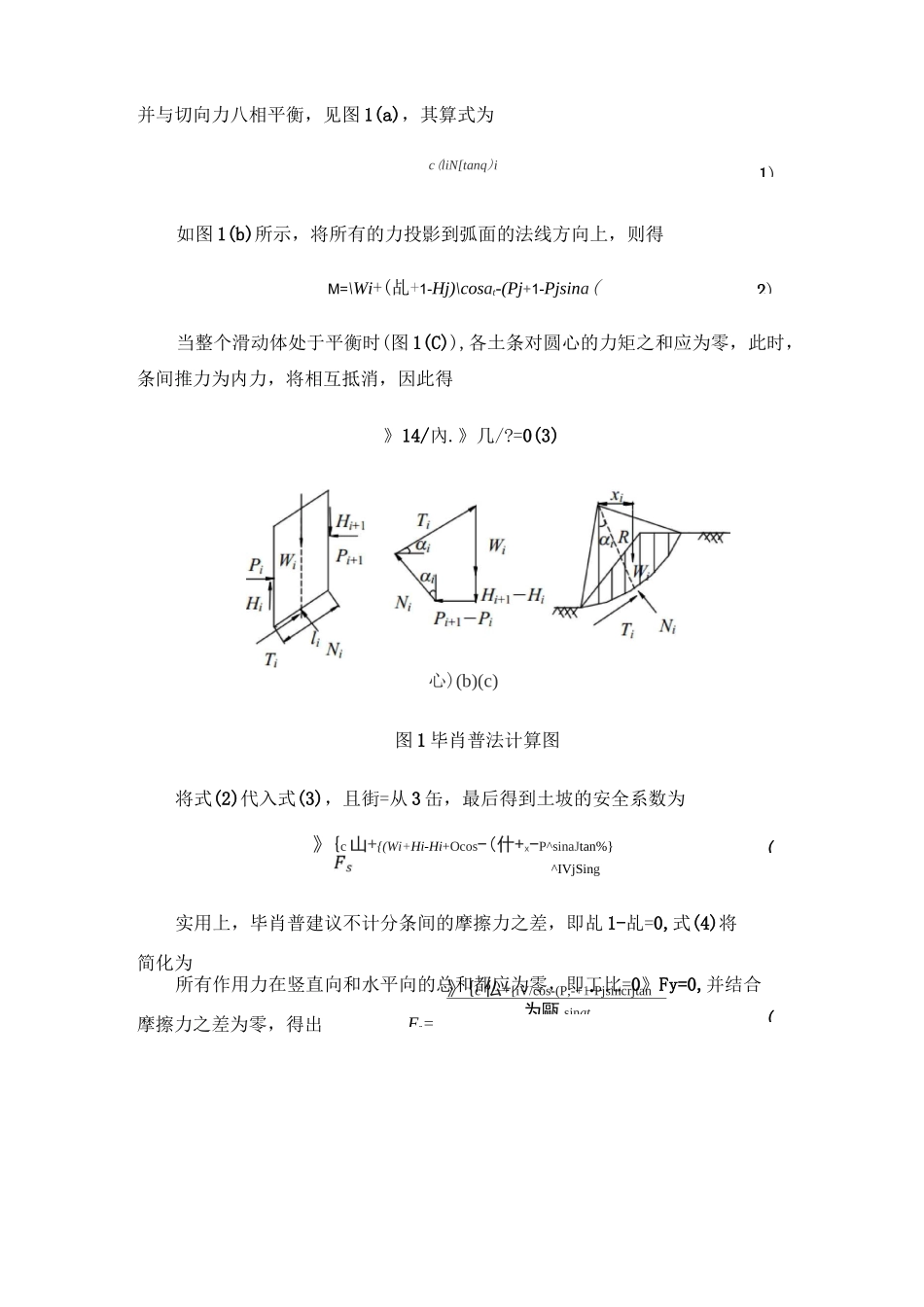
X+1tEi+WyZi+iZ基于极限平衡法原理的边坡稳定计算有多种方法,根据不同的适用条件,主要有摩根斯坦一普瑞斯(Morgenstern-Price)法、毕肖普(Bishop)法、简布(Janbu)法、推力法、萨尔玛(Sarma)法等。摩根斯坦一普瑞斯(Morgenstern-Price)法该方法考虑了全部平衡条件与边界条件,消除了计算方法上的误差,并对Janbu推导出来的近似解法提供了更加精确的解答;对方程式的求解采用数值解法(即微增量法),滑面形状任意,通过力平衡法所计算出的稳定系数值可靠程度较高。图12—1力学模型示意图根据其力学模型和几何条件以及静力平衡方程工X二0工Y二0可解得平衡条件:a+a•e+a•e•eHa•e•e…e•eK———nn_1nn_2nn~11nn_132cP+P•e+P•e•e+…+P•e•e…e•enn-1nn-2nn-11nn-132式中:e—Q[cos仰-a+q-8)sec®iibiisiisi条块侧面粘聚cs条块底面粘聚cbiP=Q•Wcos©-a)S=(C•d-PW•tanp)iaieiiisiiisiS二(C•d-PW•tnp)i+1si+1i+1i+1si+1R=(C•bseca-u•tanp)ibiiiibiQ=sec(p-a+p)cospibiisi+1si+1Pbi——条块底面摩擦角条块侧面摩擦角式(12—1)分成n块滑体达到静力平衡的条件。该式物理意义是:使滑体达到极限平衡状态,必须在滑体上施加一个临界水平加速度Kc。Kc为正时,方向向坡外,Kc为负时,方向向坡内,Kc的大小由式(12—1)确定。在对该方法应用中,对其进行了进一步完善,充分考虑了分层作用,并使不同层位赋予不同的强度参数,同时它还要求对解的合理性进行校核,使分析计算更趋合理,从而显示了该方法很强的适用性。Bishop法概述:目前,在工程上常用的两种土坡稳定分析方法仍为瑞典圆弧法(Fellenius法)和简化毕肖普法,它们均属于极限平衡法。瑞典圆弧法的土条间作用力的假设不太合理,得出的安全系数明显偏低,而简化毕肖普法的假设较为合理,计算也不复杂,因而在工程中得到了十分广泛的应用。当土坡处于稳定状态时,任一土条内滑弧面上的抗剪强度只发挥了一部分,(》{c仏+[iV/cos-(P,-+1•Pjsincrjtan为甌sinatFs=(2)1)并与切向力八相平衡,见图1(a),其算式为c(liN[tanq)i如图1(b)所示,将所有的力投影到弧面的法线方向上,则得M=\Wi+(乩+1-Hj)\cosat-(Pj+1-Pjsina(当整个滑动体处于平衡时(图1(C)),各土条对圆心的力矩之和应为零,此时,条间推力为内力,将相互抵消,因此得》14/內.》几/?=0(3)心)(b)(c)图1毕肖普法计算图将式(2)代入式(3),且街=从3缶,最后得到土坡的安全系数为》{c山+{(Wi+Hi-Hi+Ocos-(什+x-P^sinaJtan%}^IVjSing实用上,毕肖普建议不计分条间的摩擦力之差,即乩1-乩=0,式(4)将简化为所有作用力在竖直向和水平向的总和都应为零,即工比=0》Fy=0,并结合摩擦力之差为零,得出(8)(7)畑cosg+Mtan%)面両书二爲EVK/sinaLps=(ii1cihyWiCos«jtan(Pi+y~・IvasinP^+l"Pi—tan(p^——ina(+cos代入式(5),简化后得当采用有效应力法分析时,重力项"「将减去孔隙水压力"I,并采用有效应力强度指标dM有Y(c2icosaj+”畑10;);tan^sinayrs-|-cosajX^sinai在计算时,一般可先给化假定一值,采用迭代法即可求出。根据经验,通常只要迭代3~4次就可满足精度要求,而且迭代通常总是收敛的。简布(janbu)法简布(janbu)法是假定条块间的水平作用力的位置,每个条块都满足全部的静力平衡条件和极限平衡条件,滑动土体的整体力矩平衡条件也满足,而且它适用于任何滑动面而不必规定滑动面是一个圆弧面,所以又称为普遍条分法。简布(janbu)法条块作用力分析。Pi+1(8-(a)(b)(c)其中:T=丄(cl+Ntg©)(8-1)iFiiiisAP=P-P(8-2)ii+1iAH=H-H(8-3)ii+1i第i条块力平衡条件:工F=0得W+H=Nco9+Ts©n(8-4)Ziiiiii工F=0得nP=Tco©-Ns©n(8-5)Xiiiii将8-1式、8-2式、8-3式和8-5式代入到8-41式中,得^^1©^耳cos©i+(W.+H)tg©i]-(W+H”)tg©,=0Fa条块侧面的法向力P,显然有P=口P,P=P+P卞P+P,依次类推,10121口2口1口2有P召Pj=iWii8-8)8-7)若全部条块的总数为n则有p=Hp=0ii=1将8-6式代入8-7,得工[cl+(W+H)tgO]sec2liii□ii1+tg0tg©/F7.2)7.1)图7-2Sarma法力学破坏模图7-1Sarma法岩体破坏形式2)滑动力以平行于滑动面的剪应力和垂直于滑动面的正应力集中作用于滑动面上;(3)视边坡为理...