二次函数的图象(第课时)VIP免费

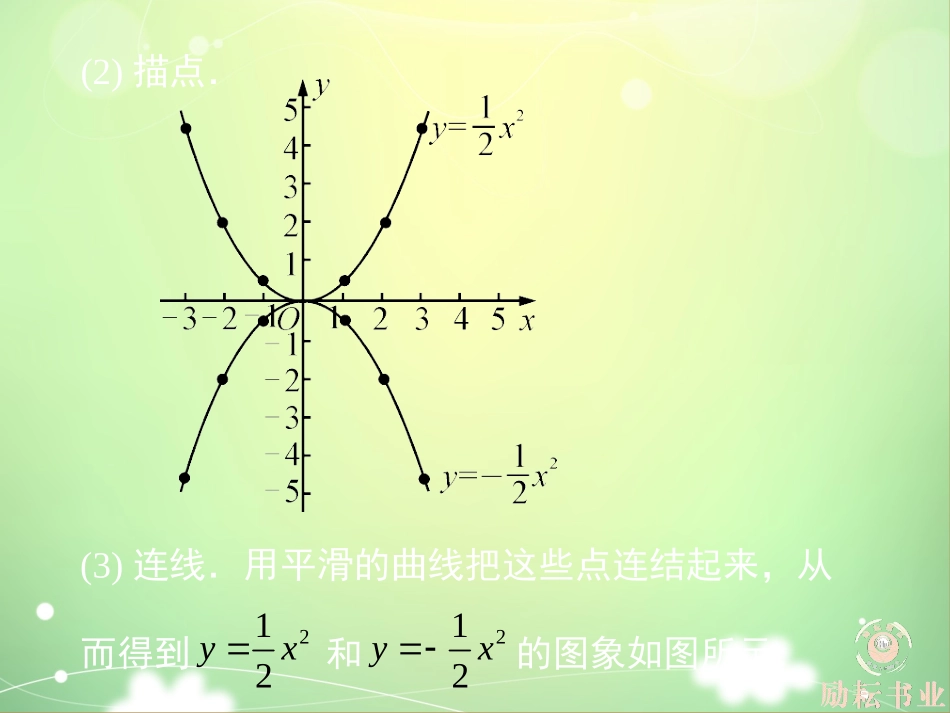
1.2二次函数的图象(第1课时)二次函数y＝ax2的图象例1在同一直角坐标系中，画出二次函数和的图象，并说明两个图象有何关系．212yx212yx上册第1章二次函数解析：(1)列表：x…-3-2-10123……202……-20-2…212yx212yx9292121212129292(3)连线．用平滑的曲线把这些点连结起来，从而得到和的图象如图所示．(2)描点．212yx212yx答案：见解析．反思：从表格中发现：横向看，x互为相反数，y的值相等；纵向看，相等的x，两y的值互为相反数．二次函数的图象，从横向看的图象是轴对称图形，从纵向看，和的图象关于x轴对称．连线注意中间顶点的光滑和末端的出头两个细节．212yx212yx212yx变式：不画图象，你能否猜想y＝－2x2的大致形状，并描述它？答案：顶点为原点，图象在x轴下方(除顶点外)，对称轴为y轴，与y＝2x2关于x轴对称．二次函数y＝ax2图象的性质例2已知抛物线y＝ax2(a≠0)的图象经过点A(－2，－8)．(1)求此抛物线的函数解析式；(2)说出这个二次函数图象的顶点坐标、对称轴、开口方向和图象的位置；(3)判断点B(－1，－4)，C(2，－8)是否在此抛物线上？解析：(1)把点A(－2，－8)的坐标代入y＝ax2，得－8＝4a，∴a＝－2.∴抛物线的解析式为y＝－2x2；(2)二次函数y＝－2x2的图象为抛物线，其顶点为(0，0)，对称轴为y轴，∵－2＜0，∴这个二次函数的图象开口向下，顶点是图象的最高点，图象在x轴的下方(除顶点外)；(3)当x＝－1时，y＝－2×(－1)2＝－2≠－4；当x＝2时，y＝－2×22＝－8.∴点B不在此抛物线上，点C在此抛物线上．答案：(1)y＝－2x2；(2)顶点(0，0)，对称轴为y轴，开口向下，图象在x轴下方(除顶点外)；(3)点B不在此抛物线上，点C在此抛物线上．例3小桥的桥孔形状是一条开口向下的抛物线.(1)画出该抛物线；(2)当水平面离开抛物线顶点2个单位时，水面宽是多少个单位？(3)当水面宽度为6个单位长度时，水面离抛物线顶点的距离是多少个单位长度？应用二次函数y＝ax2的图象解决实际问题212yx解析：(1)用描点法画，如图(2)当y＝－2时，解得x1＝2，x2＝－2,∴水面宽＝2－(－2)＝4；212,2x(3)当x＝3时，，∴当水面宽度为6个单位长度时，水平面离抛物线顶点距离是个单位长度．答案：(1)如图；(2)4；(3)反思：本题属于用函数图象解决实际问题，这类题渗透了“数”与“形”的结合，抓住“数”与“形”之间的转化是解决问题的关键．219322y929.2变式：如图是一抛物线形的拱桥，桥顶O离水面4m，水面宽度AB为10m．现有一竹排运送一只货箱欲从桥下经过，已知货箱长10m，宽6m，高2.55m(竹排与水平面持平)．问：此货箱能否顺利通过该桥？并说明理由．答案：能顺利通过．理由：以桥顶O为原点建立如图所示的平面直角坐标系，则点A的坐标为(－5，－4)．设抛物线的表达式为y＝ax2，则－4＝25a，∴∴∵货箱高2.55m，∴货箱顶部离桥顶4－2.55＝1.45(m)．当y＝－1.45时，∴16x2＝145.∴∴货箱能顺利通过该桥．4,25a24.25yx145144122||6,222x,45.12542x例下面照片上的拱门是美国密苏里州圣路易斯市的一个标志性建筑，该拱门的形状是一条抛物线，抛物线的宽和高都是190m(见照片右方的图)．请按图中所建立的直角坐标系，求出这条抛物线的解析式．并求出在离地面100m高处拱门的宽度．错解：设y＝ax2，把B(95，－190)代入得∴把y＝－100代入得，∴离地100m处拱门宽度为m.正解：把y＝－90代入得∴离地100m处拱门宽度为m.错因：由题到图可知AB是地面，错误的原因是把x轴当作地面．离地100米处点的纵坐标不是－100而是－90.x=5190,1019022y=,95xx=1519,3019,952a,9522xy