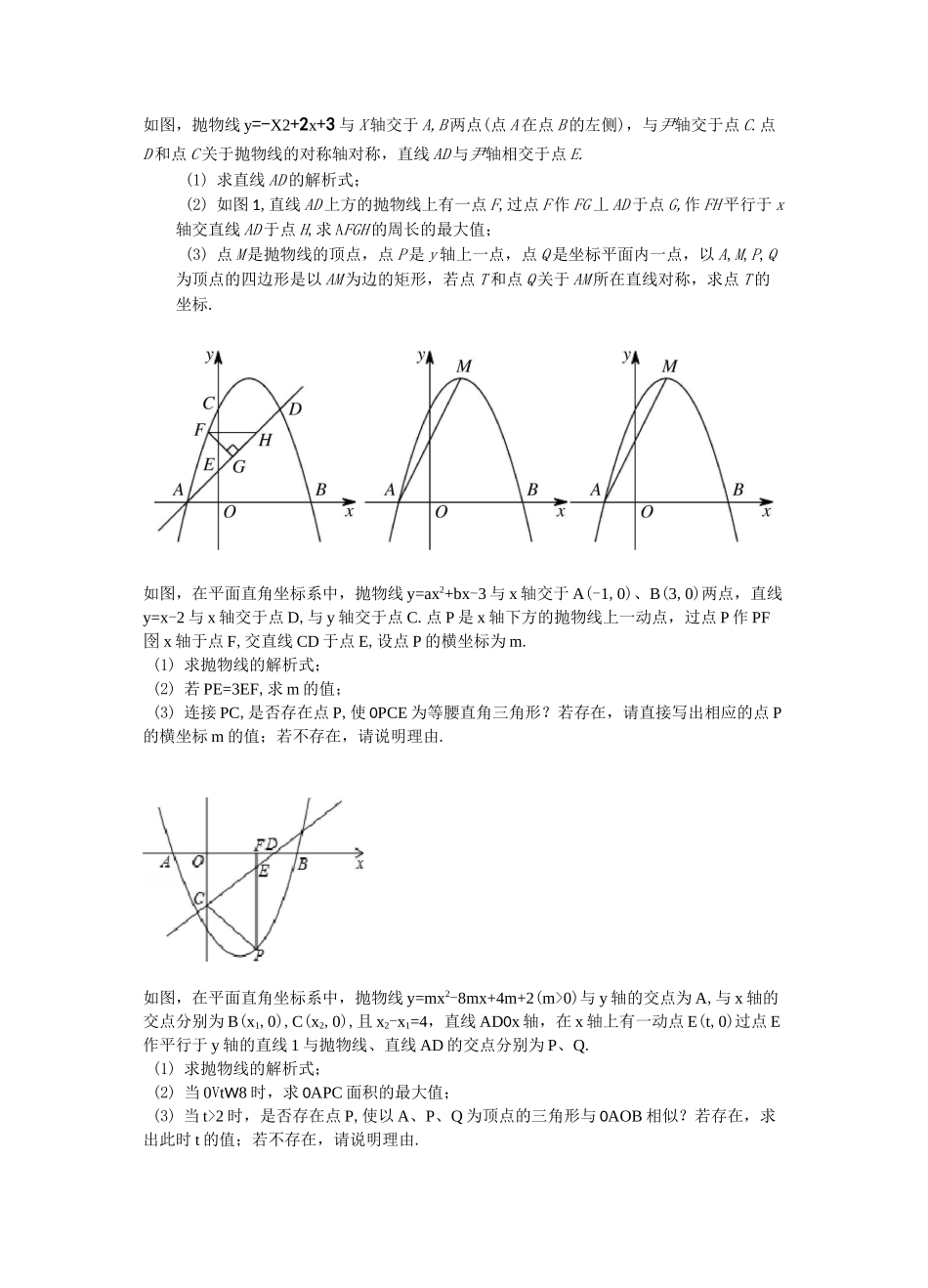
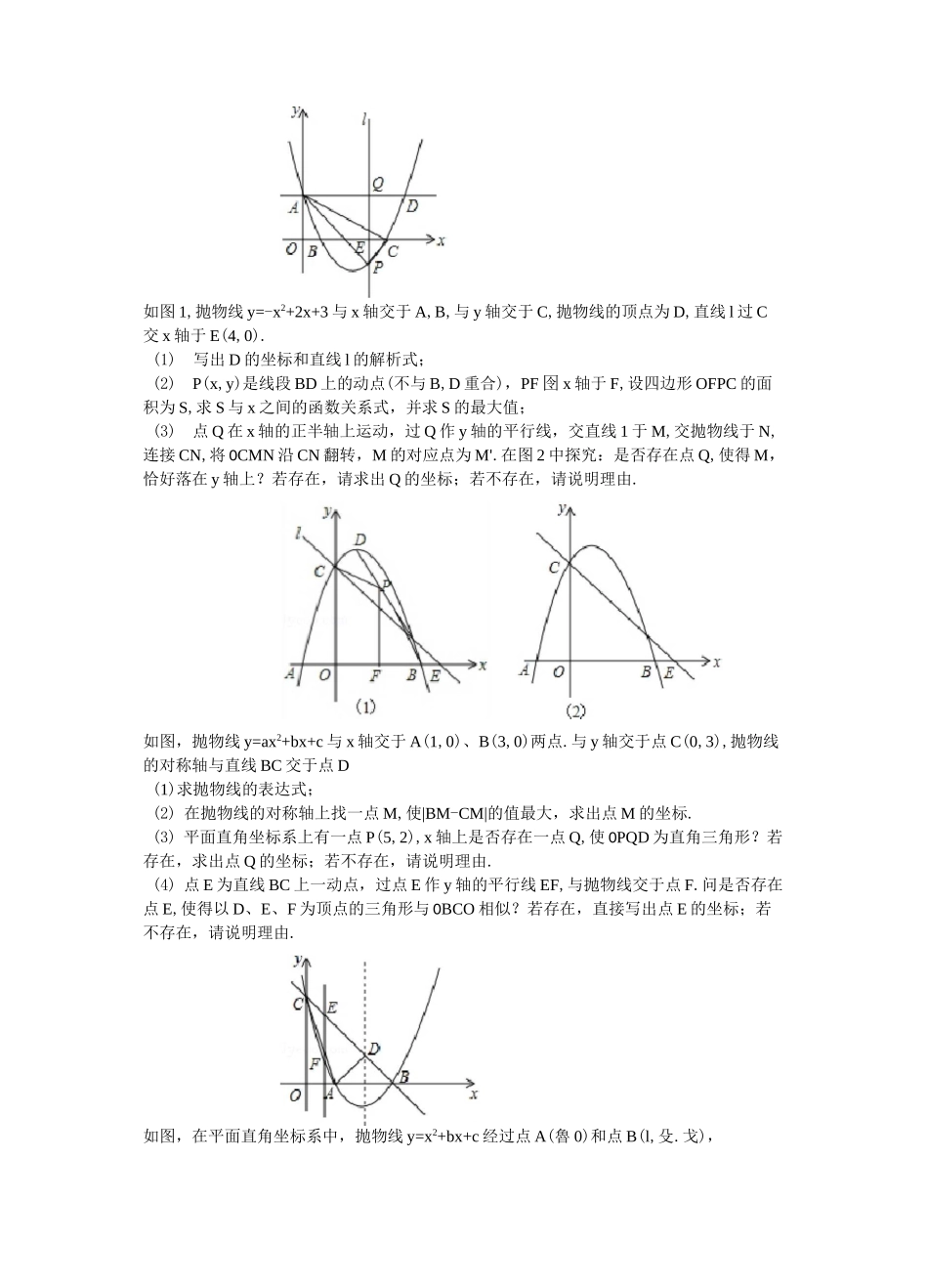
如图,抛物线y=-X2+2x+3与X轴交于A,B两点(点A在点B的左侧),与尹轴交于点C.点D和点C关于抛物线的对称轴对称,直线AD与尹轴相交于点E.(1)求直线AD的解析式;(2)如图1,直线AD上方的抛物线上有一点F,过点F作FG丄AD于点G,作FH平行于x轴交直线AD于点H,求AFGH的周长的最大值;(3)点M是抛物线的顶点,点P是y轴上一点,点Q是坐标平面内一点,以A,M,P,Q为顶点的四边形是以AM为边的矩形,若点T和点Q关于AM所在直线对称,求点T的坐标.如图,在平面直角坐标系中,抛物线y=ax2+bx-3与x轴交于A(-1,0)、B(3,0)两点,直线y=x-2与x轴交于点D,与y轴交于点C.点P是x轴下方的抛物线上一动点,过点P作PF囹x轴于点F,交直线CD于点E,设点P的横坐标为m.(1)求抛物线的解析式;(2)若PE=3EF,求m的值;(3)连接PC,是否存在点P,使0PCE为等腰直角三角形?若存在,请直接写出相应的点P的横坐标m的值;若不存在,请说明理由.如图,在平面直角坐标系中,抛物线y=mx2-8mx+4m+2(m>0)与y轴的交点为A,与x轴的交点分别为B(x1,0),C(x2,0),且x2-x1=4,直线AD0x轴,在x轴上有一动点E(t,0)过点E作平行于y轴的直线1与抛物线、直线AD的交点分别为P、Q.(1)求抛物线的解析式;(2)当0VtW8时,求0APC面积的最大值;(3)当t>2时,是否存在点P,使以A、P、Q为顶点的三角形与0AOB相似?若存在,求出此时t的值;若不存在,请说明理由.如图1,抛物线y=-x2+2x+3与x轴交于A,B,与y轴交于C,抛物线的顶点为D,直线l过C交x轴于E(4,0).(1)写出D的坐标和直线l的解析式;(2)P(x,y)是线段BD上的动点(不与B,D重合),PF囹x轴于F,设四边形OFPC的面积为S,求S与x之间的函数关系式,并求S的最大值;(3)点Q在x轴的正半轴上运动,过Q作y轴的平行线,交直线1于M,交抛物线于N,连接CN,将0CMN沿CN翻转,M的对应点为M'.在图2中探究:是否存在点Q,使得M,恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.如图,抛物线y=ax2+bx+c与x轴交于A(1,0)、B(3,0)两点.与y轴交于点C(0,3),抛物线的对称轴与直线BC交于点D(1)求抛物线的表达式;(2)在抛物线的对称轴上找一点M,使|BM-CM|的值最大,求出点M的坐标.(3)平面直角坐标系上有一点P(5,2),x轴上是否存在一点Q,使0PQD为直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.(4)点E为直线BC上一动点,过点E作y轴的平行线EF,与抛物线交于点F.问是否存在点E,使得以D、E、F为顶点的三角形与0BCO相似?若存在,直接写出点E的坐标;若不存在,请说明理由.如图,在平面直角坐标系中,抛物线y=x2+bx+c经过点A(魯0)和点B(l,殳.戈),52与x轴的另一个交点为C.(1)求抛物线的函数表达式;(2)点D在对称轴的右侧,x轴上方的抛物线上,且0BDA=0DAC,求点D的坐标;(3)在(2)的条件下,连接BD,交抛物线对称轴于点E,连接AE.①判断四边形OAEB的形状,并说明理由;②点F是OB的中点,点M是直线BD的一个动点,且点M与点B不重合,当囹BMF^^MFOB的右侧),与y轴交于点C,点A的坐标为(4,0),抛物线的对称轴是直线x^.(1)求抛物线的解析式;(2)M为第一象限内的抛物线上的一个点,过点M作MG0x轴于点G,交AC于点H,当线段CM=CH时,求点M的坐标;(3)在(2)的条件下,将线段MG绕点G顺时针旋转一个角a(0°VaV90°),在旋转过程中,设线段MG与抛物线交于点N,在线段GA上是否存在点P,使得以P、N、G为顶点的三角形与囹ABC相似?如果存在,请求出点P的坐标;如果不存在,请说明理由.B/OS/o音用如图,二次函与x轴交于A、B两点,与y轴交于C点,点P从A点出发,以1个单位秒的速度向点B运动,点Q同时从C点出发,以相同的速度向y轴正方向运动,运动时间为t秒,点P到达B点时,点Q同时停止运动.设PQ交直线AC于点G.(1)求直线AC的解析式;(2)设囹PQC的面积为S,求S关于t的函数解析式;(3)在y轴上找一点M,使囹MAC和0MBC都是等腰三角形.直接写出所有满足条件的M点的坐标;(4)过点P作PE0AC,垂足为E,当P点运动时,线段EG的长度是否发生改变,请说明理由.如图,直线y=2x+2与x轴交于点A,与y轴交于点B,把囹AOB沿y轴翻折,点A落到点C,过点B的抛物线y=-x2+bx+c与直线BC交于点D(3,-4).(1)求直线BD和抛物线的解析式;(2)在第一象限内的抛物线上,是否存在一点M,作MN垂直于x轴,垂足为...