一元二次方程根与系数的关系VIP免费

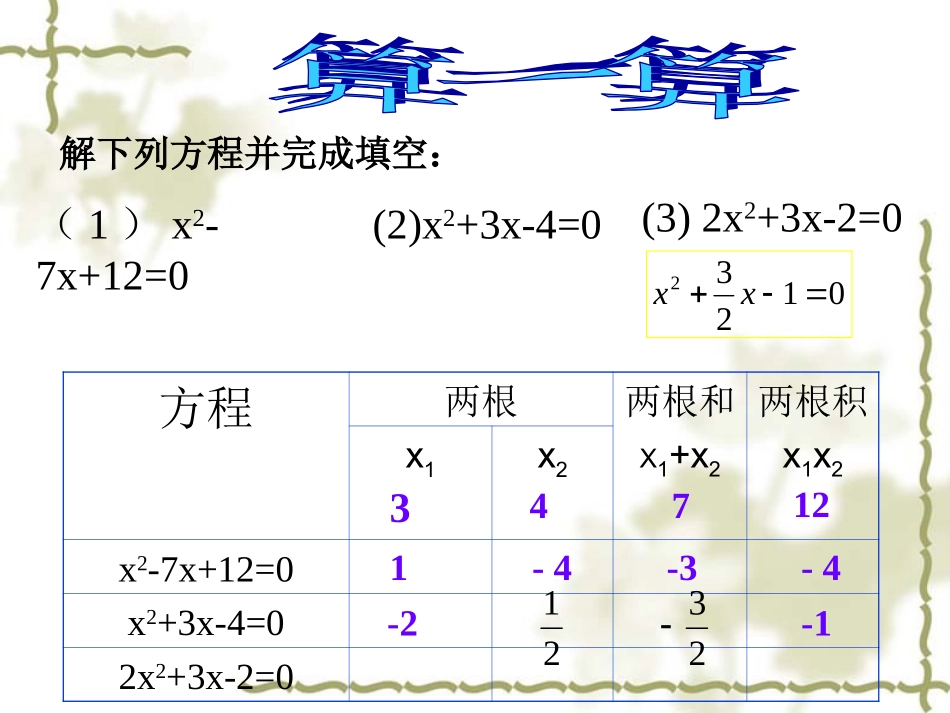
一元二次方程ax2+bx+c=0(a≠0)的求根公式：x=aacbb242(b2-4ac≥0)（1）x2-7x+12=0(2)x2+3x-4=0(3)2x2+3x-2=0解下列方程并完成填空：方程两根两根和X1+x2两根积x1x2x1x2x2-7x+12=0x2+3x-4=02x2+3x-2=0341271-3-4-4-1-2212301232xx一元二次方程的根与系数的关系：如果方程ax2+bx+c=0(a≠0)的两个根是x1,x2,那么x1+x2=,x1x2=abac（韦达定理）注：能用根与系数的关系的前提条件为b2-4ac≥00x2acxab韦达（1540－1603）韦达是法国十六世纪最有影响的数学家之一。第一个引进系统的代数符号，并对方程论做了改进。他生于法国的普瓦图。年青时学习法律当过律师，后从事政治活动，当过议会的议员，在对西班牙的战争中曾为政府破译敌军的密码。韦达还致力于数学研究，第一个有意识地和系统地使用字母来表示已知数、未知数及其乘幂，带来了代数学理论研究的重大进步。韦达讨论了方程根的各种有理变换，发现了方程根与系数之间的关系（所以人们把叙述一元二次方程根与系数关系的结论称为“韦达定理”）。韦达在欧洲被尊称为“代数学之父”。一元二次方程根与系数关系的证明：aacbbx2421aacbbx2422X1+x2=aacbb242aacbb242+=ab22=abX1x2=aacbb242aacbb242●=242)42(2)(aacbb=244aac=ac（1）下列方程两根的和与两根的积各是多少？2310xx2322xx2230xx231x；②③；④①我能行1(7)X2－2X=2(8)X2+5X-10=006292xx）（（10）6x2－3x＋2＝0练习题１、口答不解方程，求下列方程的两根和与两根积。⑴.X2－3X+1=0⑵.X2－2X=2（3).X2+5X-10=0如果方程x2+px+q=0的两根是x1，x2，那么x1+x2=,x1x2=－Pq例1、不解方程，求方程两根的和与两根的积：①2310xx22410xx②123xx121xx122xx解：①②原方程可化为：02122xx2121xx二次项不是1，可以先把它化为1（1）下列方程两根的和与两根的积各是多少？2310xx2322xx2230xx231x；②③；④①我能行1(7)X2－2X=2(8)X2+5X-10=006292xx）（（10）6x2－3x＋2＝01625x35[()2]75kk357答：方程的另一个根是，的值是。2560xkxk例2、已知方程求它的另一个根及的一个根是2的值。26055kxx原方程可化为：想一想，还有其他方法吗？还可以把代入方程的两边，求出2xk解：，那么1x设方程的另一根是135x∴3()255k我能行2如果2是方程的一个根，则另一个根是___ｍ=____。（还有其他解法吗？)062mxx81、求方程中的待定系数42．已知x＝1是方程x2＋bx－2＝0的一个根，则方程的另一个根是（）CA．1B．2C．－2D．－1求它的另一个根及3.已知方程23190xxmm的值。的一个根是1，1232xx1212xx22310xx例3、不解方程，求一元二次方程两个根的①平方和；②倒数和。12,xx设方程的两根是，那么①②解：我能行32221212212)(xxxxxx2122122212)(xxxxxx413)21(2)23(22221xx21212111xxxxxx)21()23(321xx411412则：21xx2221xx221)(xx＝221)(xx221)(xx＝另外几种常见的求值另外几种常见的求值2111.1xx2121xxxx)1)(1.(321xx1)(2121xxxx1221.2xxxx212221xxxx21212212)(xxxxxx12,xx22430xx12(1)(1)xx2112xxxx是方程不解方程，求下列各式的值:2.设的两个根,①②3、解答已知关于x的方程012)1(2mxmx当m=时,此方程的两根互为相反数.当m=时,此方程的两根互为倒数.－11分析:1.10121mmxx，2.111221mmxx，4、已知方程的两个实数根是且求k的值。解：由根与系数的关系得X1+X2=-k，X1×X2=k+2又X12+X22=4即(X1+X2)2-2X1X2=4K2-2(k+2）=4K2-2k-8=0 △=K2-4k-8当k=4时，△＜0当k=-2时，△＞0∴k=-2解得k=4或k=－2022kkxx2,1xx42221xx5.设x1，x2是关于x的方程x2－(m－1)x－m＝0(m≠0)思路点拨：本题是对根的判别式和根与系数关系的综合考查，因为方程有两个实数根，所以Δ＝b2－4ac≥0，求出m的取求解．的两个根，且...