相似三角形的判定方法(1)VIP免费

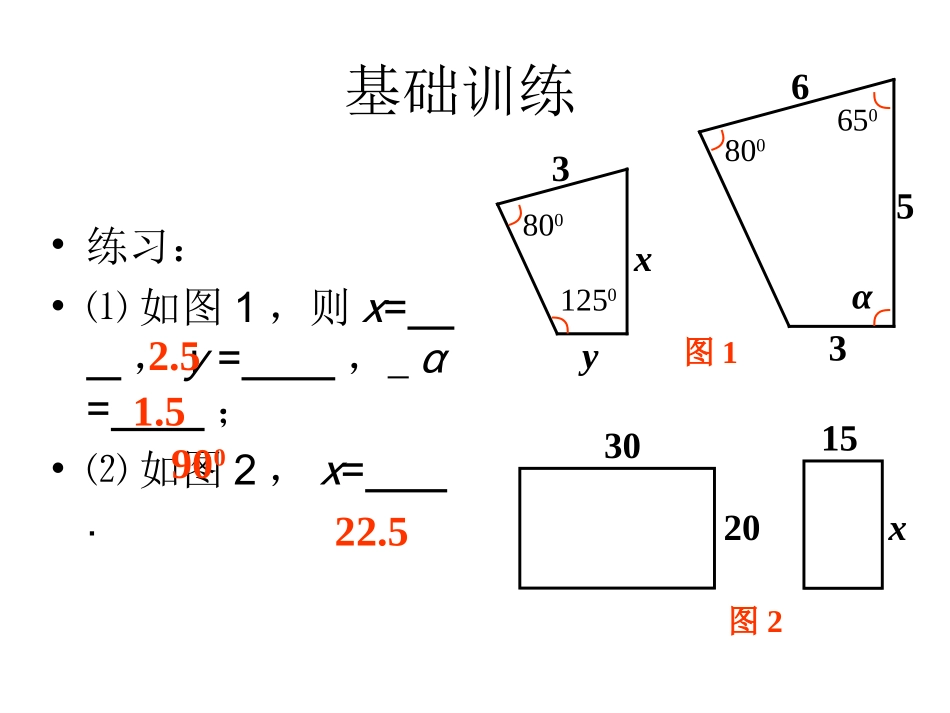
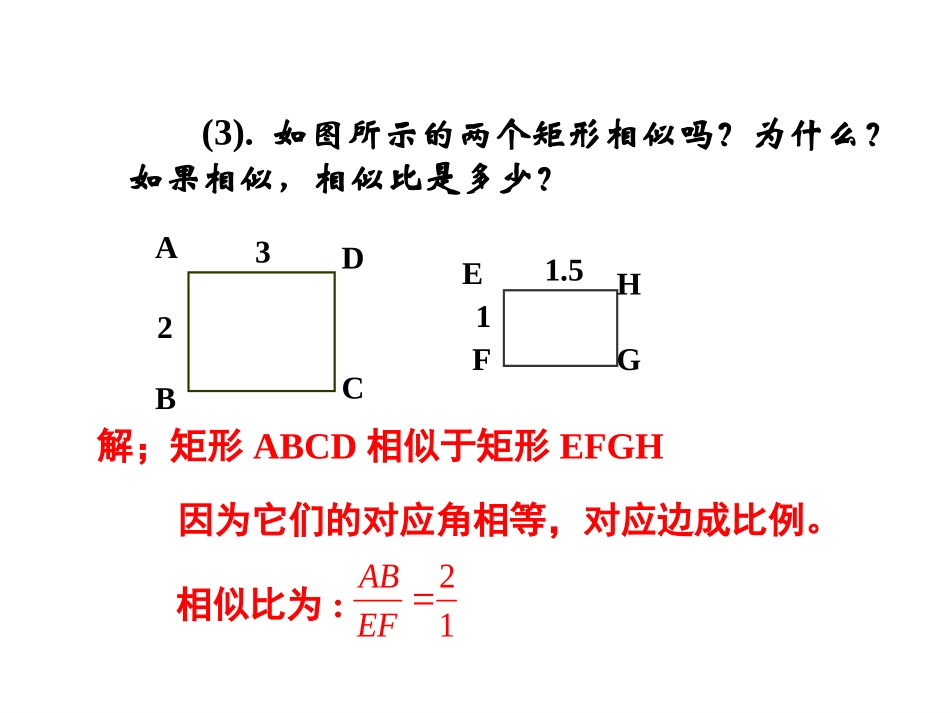
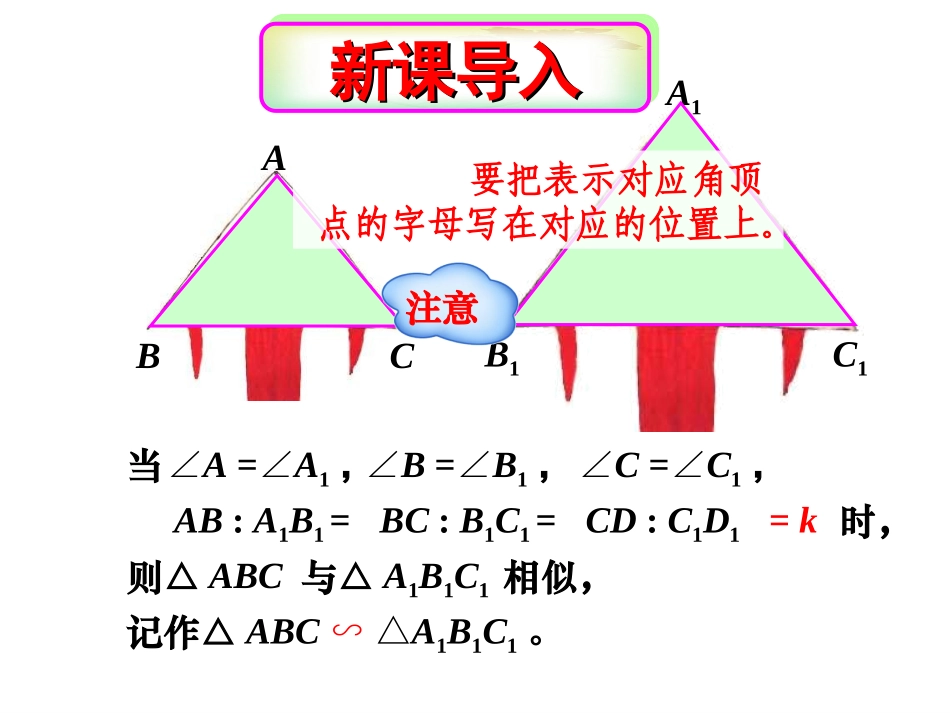
基础训练•练习：•⑴如图1，则x=，y=，α=；•⑵如图2，x=.╯800╰650╯800╮1250α╭36xy图135302015x图22.51.590022.5(3).如图所示的两个矩形相似吗？为什么？如果相似，相似比是多少？GFEH1.51ADCB32解；矩形ABCD相似于矩形EFGH因为它们的对应角相等，对应边成比例。相似比为:21ABEF新课导入新课导入新课导入新课导入ABCA1B1C1∠A=∠A1，∠B=∠B1，∠C=∠C1，AB:A1B1=BC:B1C1=CD:C1D1=k当时，则△ABC与△A1B1C1相似，记作△ABC∽△A1B1C1。要把表示对应角顶点的字母写在对应的位置上。注意相似三角形对应角相等、对应边成比例的三角形叫做相似三角形。ABCEDF相似的表示方法符号：∽读作：相似于相似比AB:A1B1=BC:B1C1=CD:C1D1=k时，ABCA1B1C1则△ABC与△A1B1C1的相似比为k.或△A1B1C1与△ABC的相似比为.1k这两个风筝图形相似，观察并思考：ABAA1B1C1大胆猜想，那么，若已知ABA∥1B1，能否得出△ABC1∽△A1B1C1ABA∥1B1除了根据相似三角形的定义来判断是否相似，还有其它的方法吗？•为了证明相似三角形的判定定理，先来学习平行线分线段成比例定理。如图,DE//BC,ADE△与△ABC有什么关系?说明理由.相似ABCDE证明:在△ADE与△ABC中∠A=∠ABCDEACAEABAD∵DE//BC∴∠ADE=B,AED=C∠∠∠过E作EF//AB交BC于F∵DBFE是平行四边形ACAEABADF∴DE=BFBCBFACAE则BCDEACAE定理：平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形相似∴△ADEABC∽△平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似。平行于三角形一边的定理ABCDE即：在△ABC中，如果DEBC∥，那么△ADEABC∽△A型你还能画出其他图形吗？平行于三角形一边的直线与其它两边(或延长线)相交,所得的三角形与原三角形________.相似“A”型“X”型（图2）DEOBCABCDE（图1）ABCDE相似具有传递性△ADEABC∽△MN如果再作MN∥DE，共有多少对相似三角形？△AMNADE∽△△AMNABC∽△共有三对相似三角形。如图，△ABC中，DE∥BC，GF∥AB，DE、ＧＦ交于点Ｏ，则图中与△ABC相似的三角形共有多少个?请你写出来.解：与△ABC相似的三角形有3个:△AＤＥ△ＧＦＣ△ＧＯＥABCDEFGO如图，在△ABC中，DGEHFIBC∥∥∥，（1）请找出图中所有的相似三角形；（2）如果AD=1，DB=3，那么DG：BC=_____。ABCDEFGHI△ADGAEHAFIABC∽△∽△∽△1：4如图,已知DEBC,AE=50cm,EC=30cm,BC=70cm,∥∠BAC=450,ACB=40∠0.(1)求∠AED和∠ADE的大小;(2)求DE的长.（2）).(75.4330507050,.70305050,cmDEDEBCDEACAE所以即ADBEC解:(1)DEBC∥△ADEABC∽△∠AED=C=40∠0.△ADEABC∽△在△ADE中,ADE=180∠0-400-450=950.