山东省冠县武训高级中学七年级数学上册两类角度计算问题同步练习1VIP免费

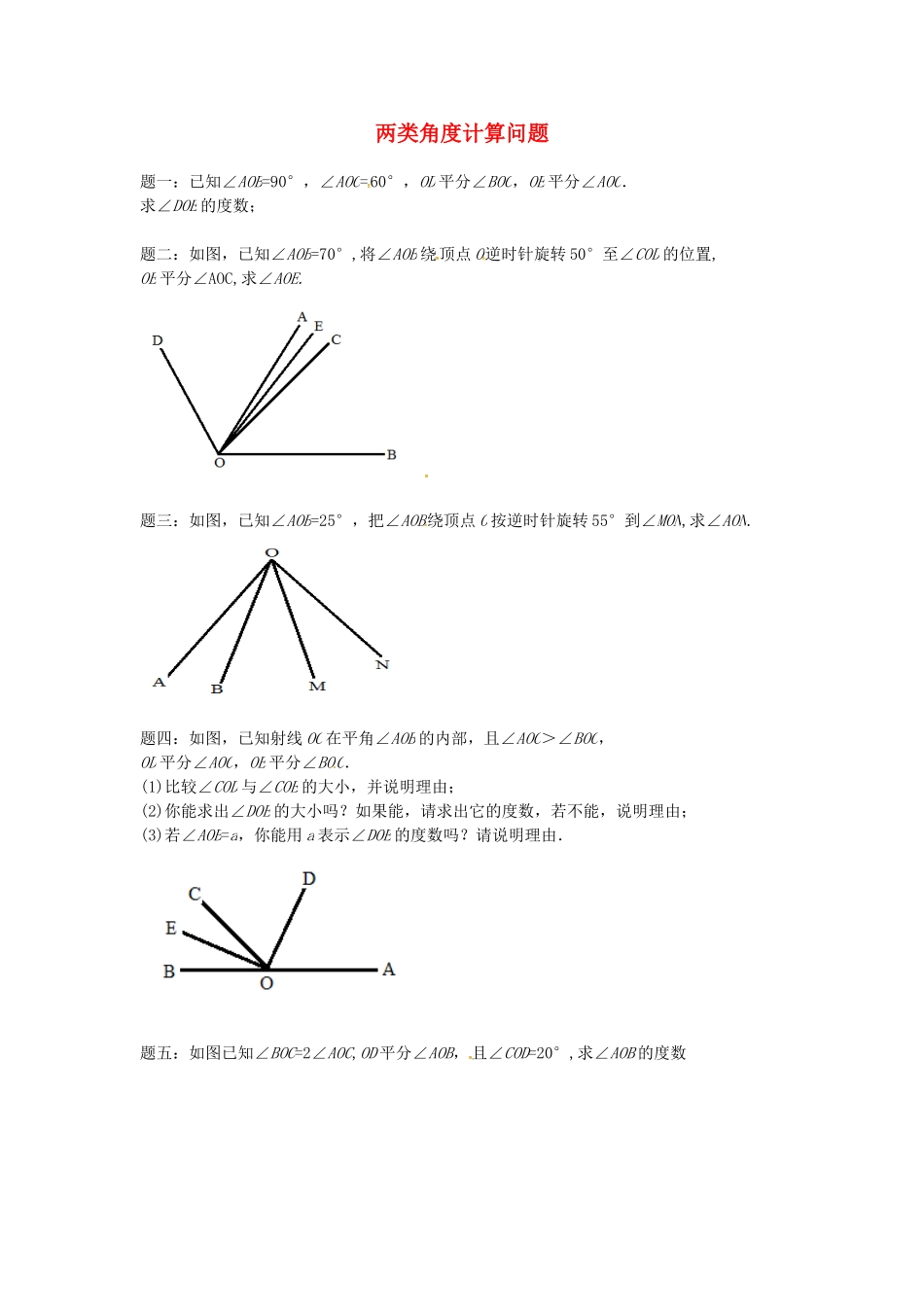
两类角度计算问题题一：已知∠AOB=90°，∠AOC=60°，OD平分∠BOC，OE平分∠AOC．求∠DOE的度数；题二：如图，已知∠AOB=70°,将∠AOB绕顶点O逆时针旋转50°至∠COD的位置,OE平分∠AOC,求∠AOE.题三：如图，已知∠AOB=25°，把∠AOB绕顶点O按逆时针旋转55°到∠MON,求∠AON.题四：如图，已知射线OC在平角∠AOB的内部，且∠AOC＞∠BOC，OD平分∠AOC，OE平分∠BOC．(1)比较∠COD与∠COE的大小，并说明理由；(2)你能求出∠DOE的大小吗？如果能，请求出它的度数，若不能，说明理由；(3)若∠AOB=a，你能用a表示∠DOE的度数吗？请说明理由．题五：如图已知∠BOC=2∠AOC,OD平分∠AOB，且∠COD=20°,求∠AOB的度数题六：两块三角板的直角顶点O重叠在一起,且OB恰好平分∠COD，则∠AOD的度数是（）两类角度计算问题课后练习参考答案题一：∠DOE=45°.详解：如图1，∠AOB=90°，∠AOC=60°，OD平分∠BOC，OE平分∠AOC，∴∠COE=12∠AOC=12×60°=30°,∠DOC=12∠BOC=12(∠AOB∠AOC)=12(90°60°)=75°，∠DOE=∠DOC∠COE=75°30°=45°；如图2，∠AOB=90°，∠AOC=60°，OD平分∠BOC，OE平分∠AOC，∴∠COE=12∠AOC=12×60°=30°,∠DOC=12∠BOC=12(∠AOB∠AOC)=12(90°60°)=15°，∠DOE=∠DOC∠COE=15°30°=45°.题二：10°.详解：∵∠AOB=70°，将∠AOB绕顶点O逆时针旋转50°，∴∠COB=50°,∠AOC=∠AOB-∠COB=70°50°=20°,又∵OE平分∠AOC,∴∠AOE=12∠AOC=12×20°=10°.题三：80°.详解：∵∠AOB=∠MON=25°，∠AOM=55°，∠AON=25°55°=80°.题四：(1)∠COD﹥∠COE；(2)∠DOE=90°；(3)∠DOE=12a.详解：(1)∠COD﹥∠COE，理由如下：∵OD平分∠AOC，OE平分∠BOC，∴∠COD=12∠AOC，∠COE=12∠BOC，∵∠AOC＞∠BOC，12∠AOC＞12∠BOC，∴∠COD﹥∠COE.(2)∠DOE=90°,理由如下：∵OD平分∠AOC，OE平分∠BOC，∴∠COD=12∠AOC，∠COE=12∠BOC，∵∠AOC∠BOC=180°，∴12∠AOC12∠BOC=90°，即∠DOE=90°.(3)∠DOE=12a，思路同(2).题五：120°详解：∵∠BOC＝2∠AOC∴∠AOB＝∠AOC∠BOC＝∠AOC2∠AOC＝3∠AOC∵OD平分∠AOB，∴∠AOD＝12∠AOB＝32∠AOC，∴∠COD＝∠AOD∠AOC＝32∠AOC∠AOC＝12∠AOC，∵∠COD＝20°∴12∠AOC＝20°∴∠AOC＝40°∴∠AOB＝3∠AOC＝120°.题六：135°.详解：∵OB平分∠COD，∠COD=∠AOB=90°，∴∠BOD=45°，∴∠AOD=∠AOB∠BOD=90°45°=135°.