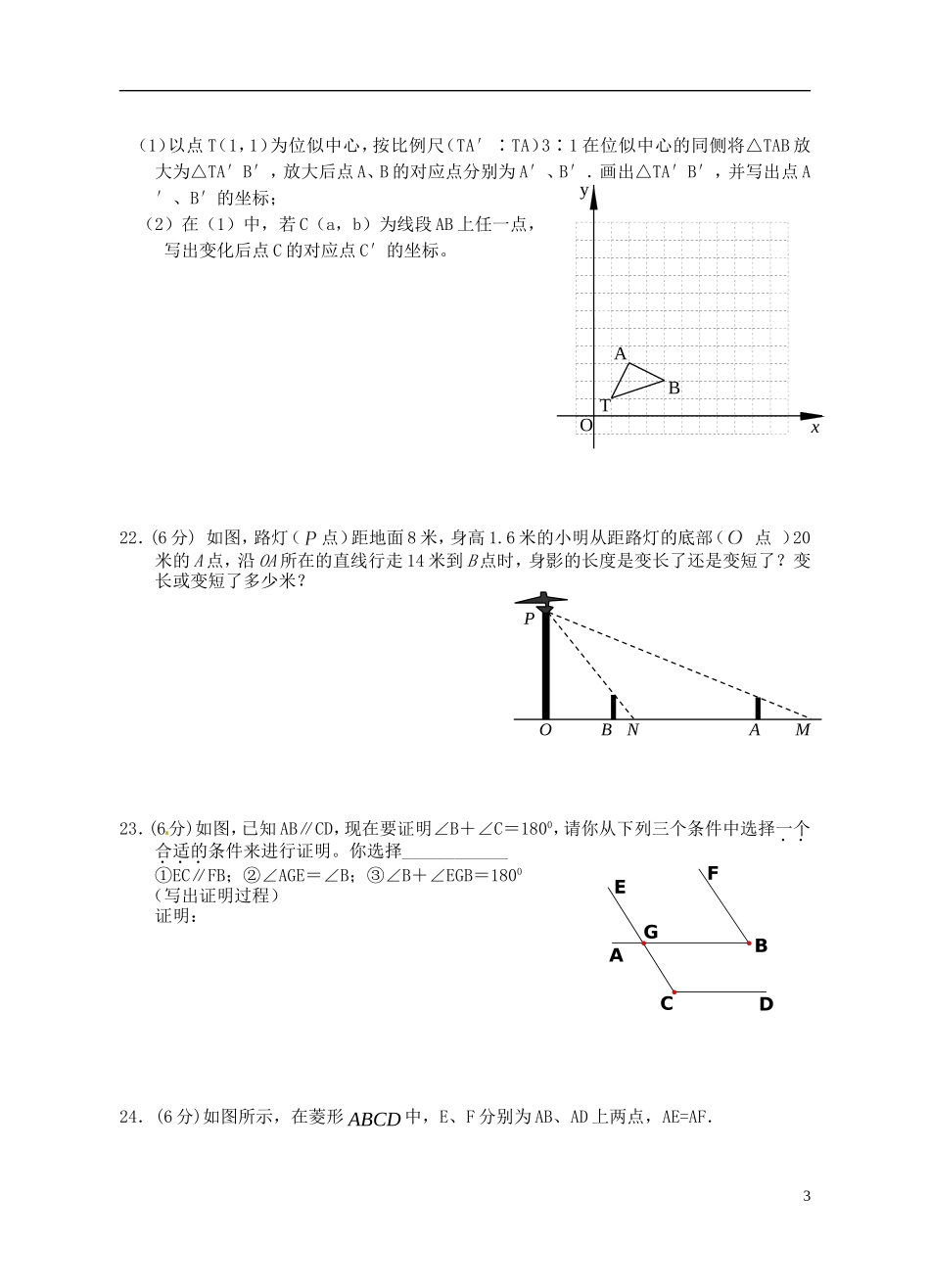
yxOPM第8题图ECDAFB第9题图江苏省昆山市兵希中学八年级数学下学期期末检测试题(B)苏科版班级姓名一、填空题(本大题共12小题,每小题3分,共36分)1.函数中自变量x的取值范围是。2.梯形ABCD中,AD∥BC,对角线AC⊥BD,且AC=12,BD=9,则此梯形的上下底之和是.3.写出命题“直角三角形中,30°角所对的边等于斜边的一半”的逆命题:;它是命题(填“真”或“假”)。4.如图,∠1=∠2,若(请补充一个条件),则△ABC∽△ADE.5.双曲线经过点(3,k)则k=.6.解方程=如果产生增根,则m=7.巡警小王在犯罪现场发现一只脚印,他把随身携带的一张百元钞票放在脚印旁进行拍照,照片送到刑事科,他们测得照片中的脚印和钞票的长度分别为5cm和3.1cm,一张百元钞票的实际长度大约为15.5cm,请问脚印的实际长度为_____________cm.8.反比例函数在第一象限内的图象如图,点M是图像上一点,MP垂直轴于点P,如果△MOP的面积为1,那么的值是9.如图,平行四边形ABCD中,E是边BC上的点,AE交BD于点F,如果23BEBC,那么BFFD.10.如图,在正三角形ABC中,D,E,F分别是BC,AC,AB上的点,DEAC⊥,EFAB⊥,FDBC⊥,则DEF△的面积与ABC△的面积之比等于.11.一个口袋中有10个红球和若干个白球。小明通过以下实验估计口袋中白球的个数:口袋中随机摸出一球,记下其颜色,再把它放回口袋中,不断重复上述过程.实验中总共摸了200次,其中有50次摸到红球.此时,小明通过计算应该得出白球有个。12.如图,正方形ABCD的面积为1,M是AB的中点,连接AC、DM,则图中阴影部分的面积是.1DCEFAB第10题图MADCB第12题图二、选择题(本大题共6小题,每小题3分,共18分)13.把分式中的x和y都扩大2倍,则分式的值()A、扩大4倍B、扩大2倍C、不变D、缩小2倍14.在比例尺为1∶16000000的江苏省地图上,某条道路的长为1.5cm.这条道路的实际长度用科学记数法表示为()A.2.4×107kmB.0.24×108kmC.2.4×102kmD.0.24×103km15.如图,直线∥,⊥.有三个命题:①;②;③.下列说法中,正确的是()(A)只有①正确(B)只有②正确(C)①和③正确(D)①②③都正确16.如图,正方形ABCD的边长为2,点E在AB边上.四边形EFGB也为正方形,设△AFC的面积为S,则()A.S=2B.S=2.4C.S=4D.S与BE长度有关17.在一个暗箱里放入除颜色外其它都相同的3个红球和11个黄球,搅拌均匀后随机任取一个球,取到是红球的概率是()A、B、C、D、18.如图,直角梯形纸片ABCD中,∠DCB=90°,AD∥BC,将纸片折叠,使顶点B与顶点D重合,折痕为CF.若AD=2,BC=5,则AF∶FB的值为()A.B.C.D.三.解答题(本大题共10题,共76分)19.(6分)解方程:20.(6分)化简求值其中21.(6分)如图,在12×12的正方形网格中,△TAB的顶点坐标分别为T(1,1)、A(2,3)、B(4,2)。2第15题图第16题第18题AFDEGBC(1)以点T(1,1)为位似中心,按比例尺(TA′∶TA)3∶1在位似中心的同侧将△TAB放大为△TA′B′,放大后点A、B的对应点分别为A′、B′.画出△TA′B′,并写出点A′、B′的坐标;(2)在(1)中,若C(a,b)为线段AB上任一点,写出变化后点C的对应点C′的坐标。22.(6分)如图,路灯(点)距地面8米,身高1.6米的小明从距路灯的底部(点)20米的A点,沿OA所在的直线行走14米到B点时,身影的长度是变长了还是变短了?变长或变短了多少米?23.(6分)如图,已知AB∥CD,现在要证明∠B+∠C=1800,请你从下列三个条件中选择一个合适的条件来进行证明。你选择____________①EC∥FB;②∠AGE=∠B;③∠B+∠EGB=1800(写出证明过程)证明:24.(6分)如图所示,在菱形ABCD中,E、F分别为AB、AD上两点,AE=AF.3TOBAxyPOBNAM(1)求证:CE=CF;(2)若∠ECF=60°,B∠=80°,试问BC=CE吗?请说明理由.25.(8分)小敏的爸爸买了某项体育比赛的一张门票,她和哥哥两人都很想去观看.可门票只有一张,读九年级的哥哥想了一个办法,拿了8张扑克牌,将数字为2、3、5、9的四张牌给小敏,将数字为4、6、7、8的四张牌留给自己,并按如下游戏规则进行:小敏和哥哥从各自的四张牌中随机抽出一张,然后将抽出的两张扑克牌数字相加,如果和为偶数...