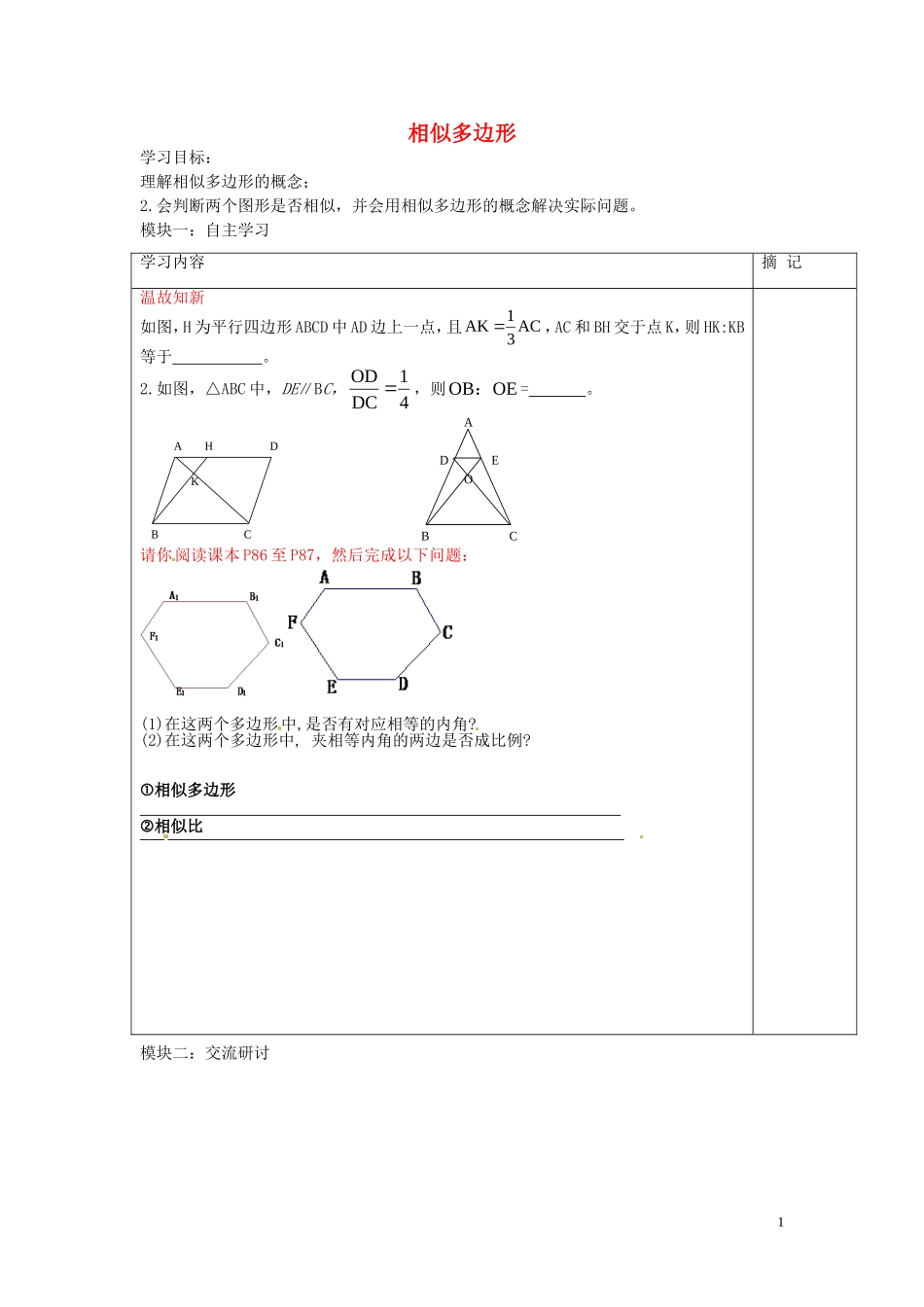
相似多边形学习目标:理解相似多边形的概念;2.会判断两个图形是否相似,并会用相似多边形的概念解决实际问题。模块一:自主学习模块二:交流研讨学习内容摘记温故知新如图,H为平行四边形ABCD中AD边上一点,且AC31AK,AC和BH交于点K,则HK:KB等于。2.如图,△ABC中,DE∥BC,41DCOD,则OEOB:=。AHDKBCADEOBC请你阅读课本P86至P87,然后完成以下问题:(1)在这两个多边形中,是否有对应相等的内角?(2)在这两个多边形中,夹相等内角的两边是否成比例?相似多边形相似比1模块三:巩固内化河源中英文实验学校两段五环讲学稿(九数上)【模块四:当堂训练】第四章§4-3相似多边形课型:新授总第4课时-8一、基础题1.两个相似多边形一组对应边分别为3cm,4.5cm,那么它们的相似比为。2.在矩形ABCD中,E,F分别为AB,CD的中点,如果矩形ABCD∽矩形EFCB,那么它们的相似比为。3.一个多边形的边长为2,3,4,5,6,另一个和它相似的多边形的最长边为24,则这个多边形的最短边长为。4.如果多边形ABCDEF∽多边形A`B`C`D`E`F`,且∠A=68°,则∠A`等于()5.两个相似多边形的最长边分别为10cm和20cm,其中一个多边形的最短边为5cm,则另一个多边形的最短边为______.二、发展题6.E,F分别为矩形ABCD的边AD,BC的中点,若矩形ABCD∽矩形EABF,AB=1.求矩形ABCD的面积。研讨内容摘记内容一:小组成员之间交换讲学稿,交换答案,看看与你的有什么不同。把你的修改意见在讲学稿上直接标注。并按照组长的分工,每位同学选择一个内容向全组同学进行交流。如有不同意见,直接提出或质疑。内容二:任意两个等边三角形相似吗?任意两个正方形呢?任意两个正n边形呢?(2)任意两个菱形相似吗?内容三:一块长3m,宽1.5m的矩形黑板,如图所示,镶在其外围的木制边框宽7.5cm,边框的内外边缘所成的矩形相似吗?为什么?学习任务摘记任务:尝试完成下列习题。如图,一个矩形广场的长为60米,宽为40米,广场内两条纵向小路的宽均为1.5米,如果设两条横向小路的宽为x米,那么当x为多少时,小路内外边缘所围成的两个矩形相似。27.对应角相等的两个多边形一定是相似多边形吗?两个多边形的对应边的比值都相等,这样的两个多边形也是相似多边形吗?三、提高题8.在长为10,宽为8的矩形ABCD中,点E在长AD上,F在AB上,若所得到的矩形EFCD∽矩形ABCD,试问AE之长是多少?请说明理由。3